Problemas resueltos de intervalo de confianza para la proporción.
1) Se selecciona aleatoriamente una muestra de 600 personas en una ciudad y se les pregunta si consideran que el tráfico en la misma es aceptablemente fluido. Responden afirmativamente 250 personas. ¿Cuál es el intervalo de confianza de la proporción de ciudadanos de esa ciudad que consideran aceptable la fluidez del tráfico, con un nivel de confianza del 90 % ?
2) Se hizo una encuesta a 325 personas mayores de 16 años y se encontró que 120 iban al teatro regularmente.
Halla, con un nivel de confianza del 94% , un intervalo para estudiar la proporción de los ciudadanos que van al teatro regularmente.3) En un control de calidad se analizó una muestra aleatoria de 750 tornillos resultando defectuosos 80 de ellos. Hallar:
a) Un intervalo de confianza para la proporción de tornillos defectuosos en el conjunto de producción con 99% de confianza.
b) ¿Cuál es el error máximo cometido en la estimación anterior?
c) Si deseamos que el error cometido, con el mismo nivel de confianza, sea la décima parte dele apartado anterior, ¿cuál ha de ser el tamaño de la muestra?4) Se desea estimar la proporción, p, de individuos daltónicos de una población a través del porcentaje observado en una muestra aleatoria de individuos, de tamaño n.
a) Si el porcentaje de individuos daltónicos en la muestra es igual al 30 % , calcula el valor de n para que, con un nivel de confianza de 0,95, el error cometido en la estimación sea inferior al 3,1 %.
b) Si el tamaño de la muestra es de 64 individuos, y el porcentaje de individuos daltónicos en la muestra es del 35 %, determina, usando un nivel de significación del 1 % , el correspondiente intervalo de confianza para la proporción de daltónicos de la población.5) En una encuesta realizada a 800 personas elegidas al azar del censo electoral, 240 declaran su intención de votar al partido A.
a) Estima, con un nivel de confianza del 95,45 % , entre qué valores se encuentra la intención de voto al susodicho partido en todo el censo.
b) Discute, razonadamente, el efecto que tendría sobre el intervalo de confianza el aumento, o la disminución, del nivel de confianza.6) Si al lanzar 80 veces una moneda se obtienen 45 caras, ¿se puede aceptar que la moneda está trucada, con un nivel de significación del 5 % ?
7) A una muestra aleatoria de 300 estudiantes de Bachillerato de determinada provincia se les preguntó si utilizaban habitualmente la bicicleta para acudir a su instituto. Sabiendo que se obtuvo 90 respuestas afirmativas, determinar justificando la respuesta:
a) El intervalo de confianza al 95 % para el porcentaje de estudiantes de Bachillerato de esa provincia que utilizaban habitualmente la bicicleta para acudir a su instituto.
b) El error máximo que cometeríamos, con una confianza del 95 %, si estimamos que dicho porcentaje es del 30 %.8) Cuatro de cada diez habitantes de una determinada población lee habitualmente el periódico Z.
Halla el intervalo característico (para el 95 %) de la proporción que leen el periódico Z, en muestras de tamaño 49.9) Tomada al azar una muestra de 60 alumnos de la universidad, se encontró que un tercio hablaban el idioma inglés.
a) Halla, con un nivel de confianza del 90 %, un intervalo para estimar la proporción de alumnos que hablan el idioma inglés entre los alumnos de la universidad.
b) A la vista del resultado anterior se pretende repetir la experiencia para conseguir una cota de error del 0,01 con el mismo nivel de confianza del 90 %. ¿Cuántos individuos ha de tener la muestra?10) En el juzgado de cierta ciudad se presentaron en el año 2005 un total de 5500 denuncias. Se seleccionó una muestra aleatoria de un 5 % de ellas. Entre las denuncias seleccionadas se determinó que 55 habían sido producidas por violencia doméstica. Determina, justificando la respuesta:
a) La estimación puntual que podríamos dar por el porcentaje de denuncias por violencia doméstica en esa ciudad en el año 2005.
b) El error máximo que cometeríamos con dicha estimación puntual con un nivel de confianza del 99 %.11) En una población de 2 000 conductores se seleccionó una muestra aleatoria de 200. A los conductores seleccionados se les preguntó si llevaban en sus vehículos cadenas para utilizar en caso de que hubiese nieve en las carreteras. A partir de la información recogida se obtuvo el siguiente intervalo de confianza al 95 % para la proporción de conductores de esa población que llevaban en sus vehículos cadenas para la nieve: (0,172 , 0,228). Determinar, justificando la respuesta:
a) La estimación puntual que daríamos para la proporción de conductores de esa población que llevan en su vehículo cadenas para la nieve.
b) El error máximo que estaríamos cometiendo, con una confianza del 95 %, con dicha estimación puntual.12) Para estimar la proporción de familias de una determinada ciudad que poseen microondas, se quiere utilizar una muestra aleatoria de medida n.
Calcula el valor mínimo de n para garantizar que, a un nivel de confianza del 95 %, el error en la estimación sea menor que 0,05. (Como se desconoce la proporción, se ha de tomar el caso más desfavorable, que será 0,5).
13) Con un nivel de confianza igual a 0,95, a partir de un estudio muestral, el intervalo de confianza de la proporción de habitantes de una comunidad que tienen ordenador portátil es { 0,1804 ; 0,2196 }.
¿Cuál es la proporción de habitantes de esa comunidad que tienen ordenador portátil?
14) Para estimar la proporción de las viviendas de una determinada ciudad que tienen aire acondicionado se quiere utilizar una muestra de tamaño n. Calcule el valor mínimo de n para que, con un nivel de confianza del 97 %, el error en la estimación sea más pequeño que 0,05.
( Como se desconoce la proporción, se debe tomar el caso más desfavorable, que será 0,5 ).
1) Se selecciona aleatoriamente una muestra de 600 personas en una ciudad y se les pregunta si consideran que el tráfico en la misma es aceptablemente fluido. Responden afirmativamente 250 personas. ¿Cuál es el intervalo de confianza de la proporción de ciudadanos de esa ciudad que consideran aceptable la fluidez del tráfico, con un nivel de confianza del 90 % ?
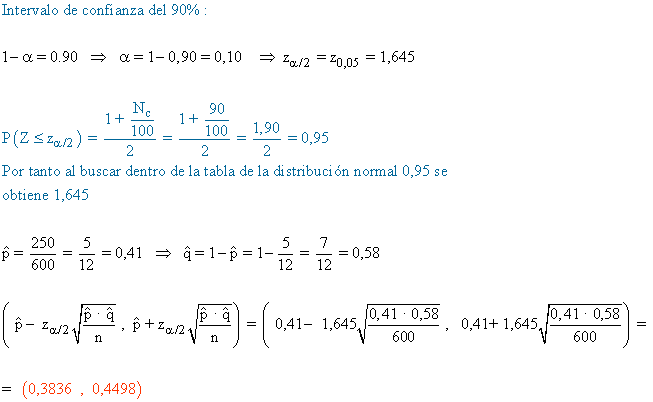
2) Se hizo una encuesta a 325 personas mayores de 16 años y se encontró que 120 iban al teatro regularmente.
Halla, con un nivel de confianza del 94%, un intervalo para estudiar la proporción de los ciudadanos que van al teatro regularmente.
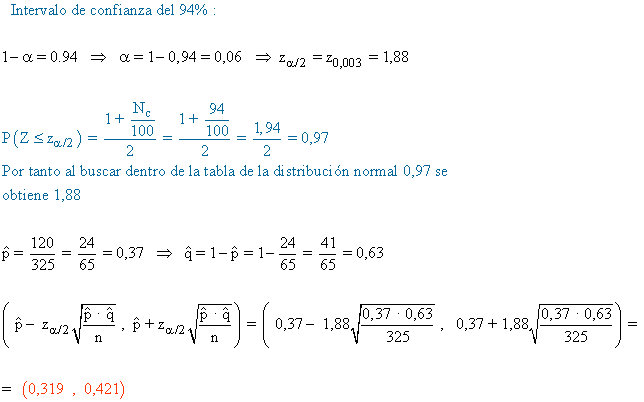
3) En un control de calidad se analizó una muestra aleatoria de 750 tornillos resultando defectuosos 80 de ellos. Hallar:
a) Un intervalo de confianza para la proporción de tornillos defectuosos en el conjunto de producción con 99 % de confianza.
b) ¿Cuál es el error máximo cometido en la estimación anterior?
c) Si deseamos que el error cometido, con el mismo nivel de confianza, sea la décima parte dele apartado anterior, ¿cuál ha de ser el tamaño de la muestra?
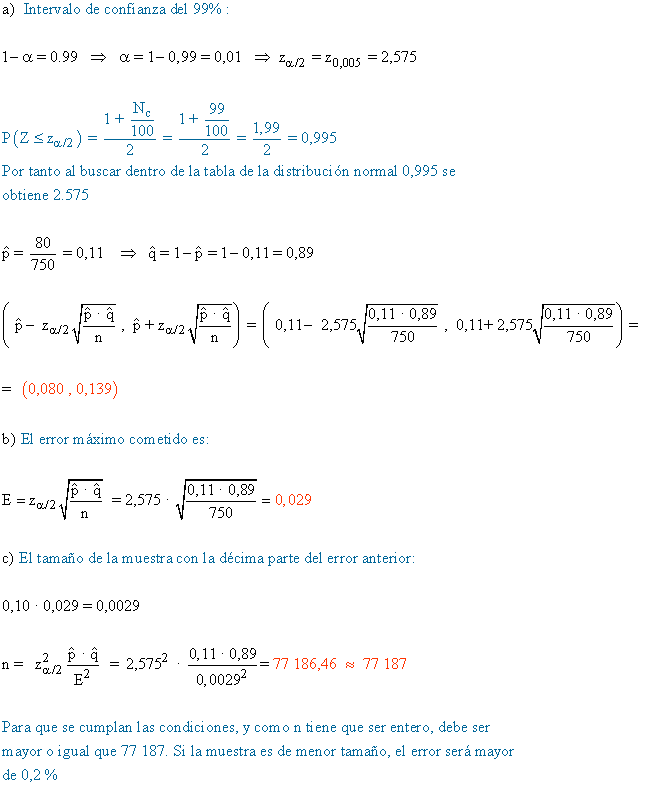
4) Se desea estimar la proporción, p, de individuos daltónicos de una población a través del porcentaje observado en una muestra aleatoria de individuos, de tamaño n.
a) Si el porcentaje de individuos daltónicos en la muestra es igual al 30 % , calcula el valor de n para que, con un nivel de confianza de 0,95, el error cometido en la estimación sea inferior al 3,1 %.
b) Si el tamaño de la muestra es de 64 individuos, y el porcentaje de individuos daltónicos en la muestra es del 35 %, determina, usando un nivel de significación del 1 % , el correspondiente intervalo de confianza para la proporción de daltónicos de la población.

5) En una encuesta realizada a 800 personas elegidas al azar del censo electoral, 240 declaran su intención de votar al partido A.
a) Estima, con un nivel de confianza del 95,45 % , entre qué valores se encuentra la intención de voto al susodicho partido en todo el censo.
b) Discute, razonadamente, el efecto que tendría sobre el intervalo de confianza el aumento, o la disminución, del nivel de confianza.

6) Si al lanzar 80 veces una moneda se obtienen 45 caras, ¿se puede aceptar que la moneda está trucada, con un nivel de significación del 5 % ?
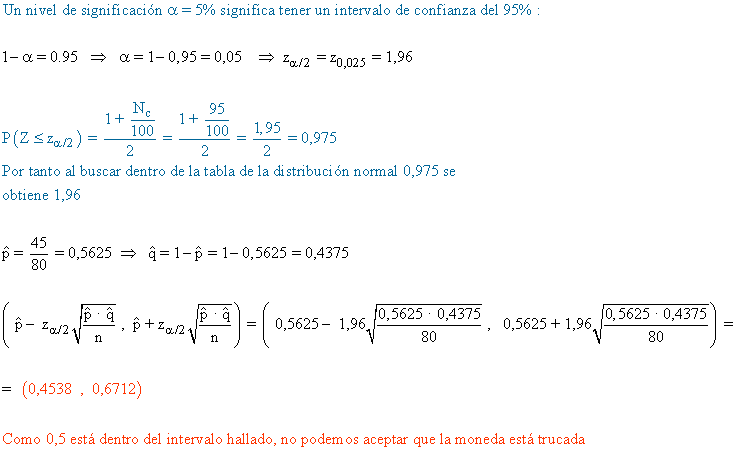
7) A una muestra aleatoria de 300 estudiantes de Bachillerato de determinada provincia se les preguntó si utilizaban habitualmente la bicicleta para acudir a su instituto. Sabiendo que se obtuvo 90 respuestas afirmativas, determinar justificando la respuesta:
a) El intervalo de confianza al 95 % para el porcentaje de estudiantes de Bachillerato de esa provincia que utilizaban habitualmente la bicicleta para acudir a su instituto.
b) El error máximo que cometeríamos, con una confianza del 95 %, si estimamos que dicho porcentaje es del 30 %.

8) Cuatro de cada diez habitantes de una determinada población lee habitualmente el periódico Z.
Halla el intervalo característico ( para el 95 % ) de la proporción que leen el periódico Z, en muestras de tamaño 49.

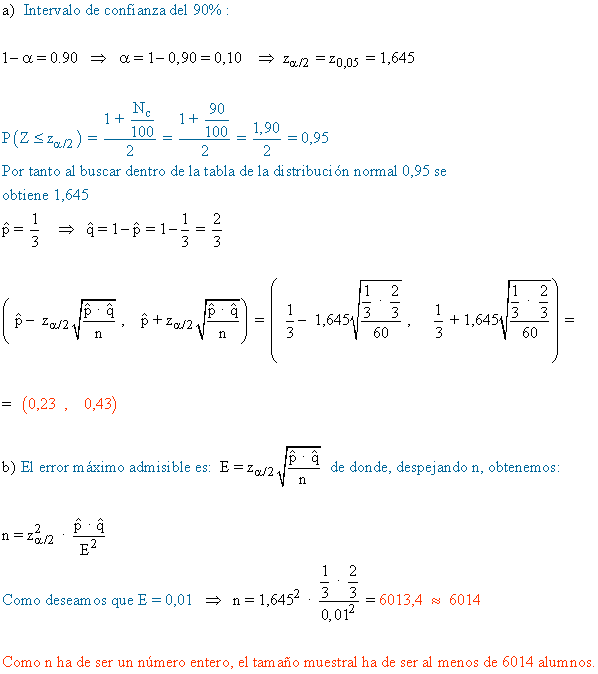
9) Tomada al azar una muestra de 60 alumnos de la universidad, se encontró que un tercio hablaban el idioma inglés.
a) Halla, con un nivel de confianza del 90 %, un intervalo para estimar la proporción de alumnos que hablan el idioma inglés entre los alumnos de la universidad.
b) A la vista del resultado anterior se pretende repetir la experiencia para conseguir una cota de error del 0,01 con el mismo nivel de confianza del 90 %. ¿Cuántos individuos ha de tener la muestra?
10) En el juzgado de cierta ciudad se presentaron en el año 2005 un total de 5500 denuncias. Se seleccionó una muestra aleatoria de un 5 % de ellas. Entre las denuncias seleccionadas se determinó que 55 habían sido producidas por violencia doméstica. Determina, justificando la respuesta:
a) La estimación puntual que podríamos dar por el porcentaje de denuncias por violencia doméstica en esa ciudad en el año 2005.
b) El error máximo que cometeríamos con dicha estimación puntual con un nivel de confianza del 99 %.
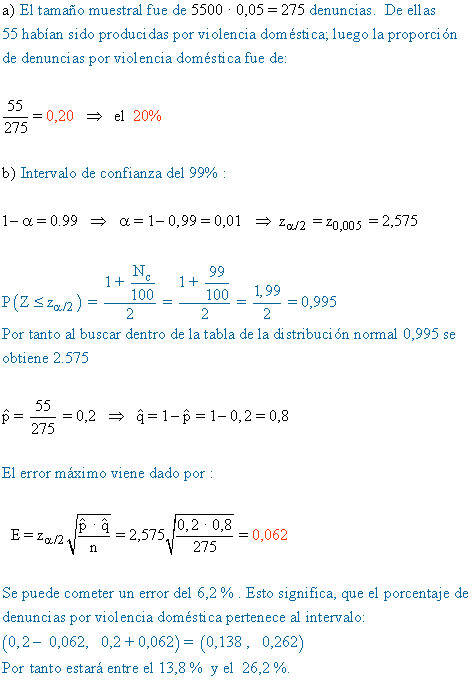
11) En una población de 2000 conductores se seleccionó una muestra aleatoria de 200. A los conductores seleccionados se les preguntó si llevaban en sus vehículos cadenas para utilizar en caso de que hubiese nieve en las carreteras. A partir de la información recogida se obtuvo el siguiente intervalo de confianza al 95 % para la proporción de conductores de esa población que llevaban en sus vehículos cadenas para la nieve: (0,172 , 0,228). Determinar, justificando la respuesta:
a) La estimación puntual que daríamos para la proporción de conductores de esa población que llevan en su vehículo cadenas para la nieve.
b) El error máximo que estaríamos cometiendo, con una confianza del 95 %, con dicha estimación puntual.

12) Para estimar la proporción de familias de una determinada ciudad que poseen microondas, se quiere utilizar una muestra aleatoria de medida n.
Calcula el valor mínimo de n para garantizar que, a un nivel de confianza del 95 %, el error en la estimación sea menor que 0,05. (Como se desconoce la proporción, se ha de tomar el caso más desfavorable, que será 0,5).
13) Con un nivel de confianza igual a 0,95, a partir de un estudio muestral, el intervalo de confianza de la proporción de habitantes de una comunidad que tienen ordenador portátil es { 0,1804 ; 0,2196 }.
¿Cuál es la proporción de habitantes de esa comunidad que tienen ordenador portátil?

14) Para estimar la proporción de las viviendas de una determinada ciudad que tienen aire acondicionado se quiere utilizar una muestra de tamaño n. Calcule el valor mínimo de n para que, con un nivel de confianza del 97 %, el error en la estimación sea más pequeño que 0,05.
( Como se desconoce la proporción, se debe tomar el caso más desfavorable, que será 0,5 ).



 INICIO
INICIO