Teorema de la altura y teorema del cateto
Triángulos rectángulos semejantes
Dos triángulos rectángulos son semejantes si tienen, al menos, un ángulo igual.
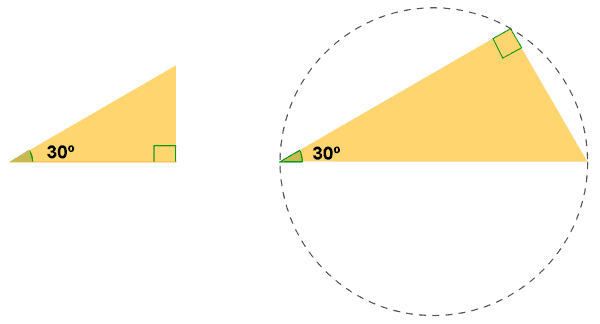
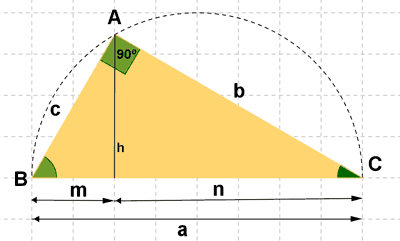
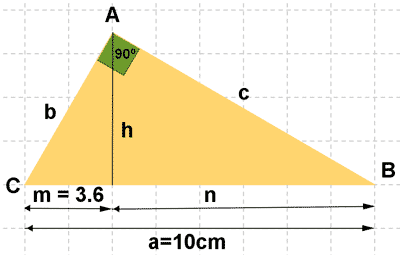
Considerando el triángulo rectángulo de la figura, ABC, con un ángulo recto en A:
• h = altura sobre la hipotenusa
• m = proyección de c sobre la hipotenusa
• n = proyección de b sobre la hipotenusa
Tres triángulos semejantes
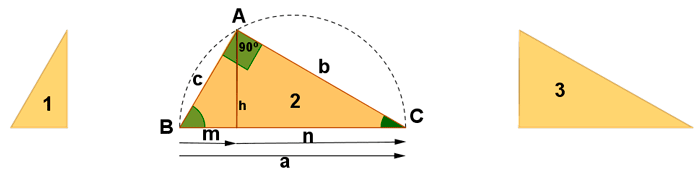
Comparando los triángulos 1 y 3 se deduce el teorema de la altura.
Comparando los triángulos 1 y 2 se deduce el teorema del cateto.
Teorema de la altura
En un triángulo rectángulo, el cuadrado de la altura sobre la hipotenusa es igual al producto de las proyecciones de los catetos sobre la hipotenusa.
![]()
Ejemplo 1 :
En un triángulo rectángulo, la altura relativa a la hipotenusa divide a ésta con longitudes de 5 cm y 14 cm. Hallar la longitud de dicha altura y dibujar el triángulo correspondiente.
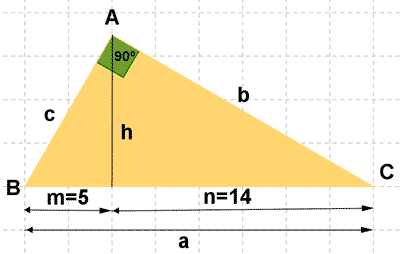
Aplicamos el teorema de la altura:
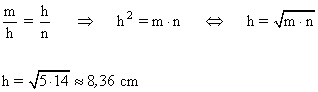
Teorema del cateto
En un triángulo rectángulo, el cuadrado de uno de los catetos es igual al producto de la hipotenusa por la proyección de ese cateto sobre la hipotenusa.
![]()
Ejemplo 2 :
En un triángulo rectángulo, la hipotenusa mide 10 cm y la proyección del cateto b sobre el mide 3,6 cm. Hallar:
a) La longitud del cateto b.
b) La longitud de la proyección del cateto c sobre la hipotenusa.
c) La longitud del cateto c.
d) La longituda de la altura relativa a la hipotenusa h.
e) Dibuja el triangulo rectángulo.
a) La longitud del cateto b.
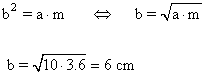
b) La longitud de la proyección del cateto c sobre la hipotenusa.
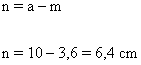
c) La longitud del cateto c.
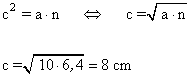
d) La longituda de la altura relativa a la hipotenusa h.
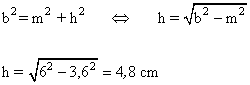
e) Dibuja el triángulo rectángulo
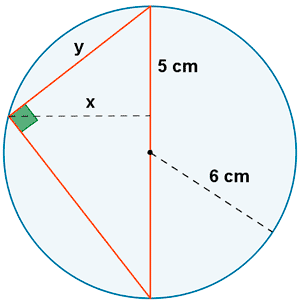
Ejemplo 3 : aplicar el teorema del cateto y de la altura.
a) Calcular x aplicando el teorema de la altura.
b) Calcular y aplicando el teorema del cateto.
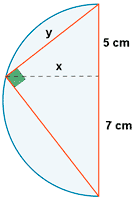
a)
El diámetro de la circunferencia es 12 cm, y como el segmento pequeño mide 5 cm, el otro segmento mide 12 - 5 = 7 cm.
Al ser un triángulo inscrito en una semicircunferencia, se trata de un triángulo rectángulo. Aplicamos entonces el teorema de la altura :
x 2 = 5 · 7 → x 2 = 35 → x = 5,92 cm
b)
Aplicamos el teorema del cateto, sabiendo que la hipotenusa mide 12 cm :
y 2 = 5 · 12 → y 2 = 60 → y = 7,75 cm


 INICIO
INICIO

