Ecuación general cuadrática de una cónica
La ecuación general cuadrática de una cónica se corresponde con una expresión de la forma:
![]()
donde al menos uno de los coeficientes A, B o C es no nulo
Al número B2 - 4·AC se llama discriminante de la ecuación, y su valor nos permite clasificar las cónicas:
| Discriminante | Cónica |
|---|---|
| Elipse o circunferencia | |
| Hipérbola | |
| Parábola |
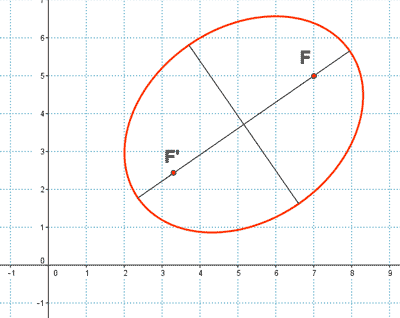
Otra definición de cónica: excentricidad
También se pueden clasificar las cónicas a través de su excentricidad:
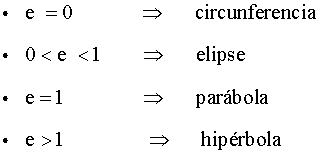
Ejemplo:
1) Clasifica las siguientes cónicas:
a) x2 + 2xy - y2 - x + 3y - 6 = 0
b) x2 + 6y + 13 = -5
c) x2 + y2 - 6x + 8y - 25 = 0
d) 4y2 - x2 = 4
e) 5x2 + 8y2 = 7


2) Clasifica las siguientes cónicas y determina sus elementos:
a) x2 + y2 - 2x + 2y + 1 = 0
b) 2x2 + 2yx2 -4x + 4y + 19 = 0
c) x2 + 4y2 = 100
d) 8x2 - 3y2 = 120
e) y2 = 36x
f) y = x2 - 2x + 3
g) x = -3y2 + y + 5
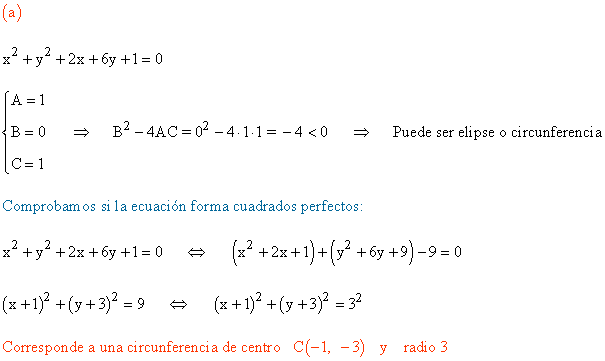

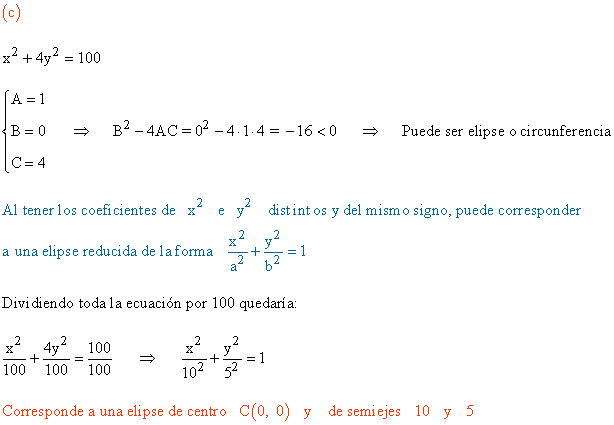


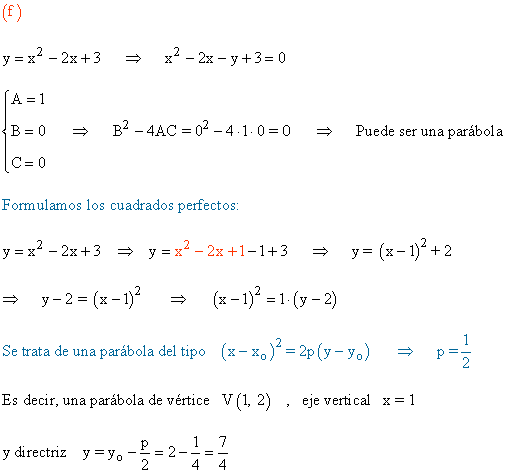



 INICIO
INICIO
