Ejercicios resueltos de circunferencias II
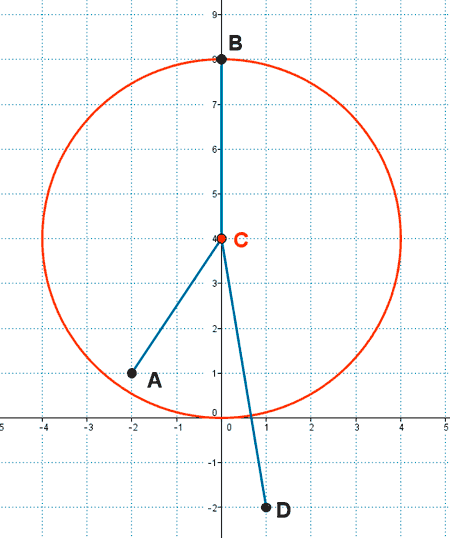
1 ) Halla la potencia de los puntos A( -2 , 1 ) , B( 0 , 8 ) , D( 1 , -2 ) respecto de la circunferencia C : x² + y²- 8y = 0 . De acuerdo con sus resultados decide su posición relativa.
2 ) Halla el eje radical de las siguientes circunferencias.
a ) C1 : x² + y ² + 2x - 3y + 1 = 0
b ) C2 : x² + y ² + 5x = 0
Comprueba que es una recta perpendicular a la línea de sus centros.
3 ) Halla el eje radical de las siguientes circunferencias.
a ) C1 : x² + y ² - 8x = 0
b ) C2 : 2x² + 2y² - 6x - 16y - 20 = 0
4 ) Halal los ejes radicales y el centro radical de las circunferencias:
C1: x2 + y2 - 4x - 2y - 4 = 0
C2: x2 + y2 - 14x - 8y + 49 = 0
C3: x2 + y2 - 14x + 4y + 37 = 0
5 ) Dada la circunferencia de ecuación x2 + y2 - 12x + 10y - 11 = 0 , Calcular las rectas tangentes a ella que son paralelas a la recta x + y + 4 = 0 .
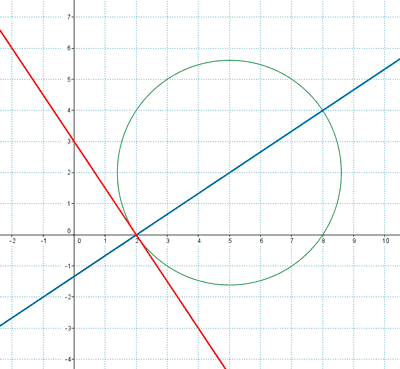
6 ) Hallar las ecuaciones de las rectas tangente y normal a la circunferencia x2 + y2 - 10x - 4 y + 16 = 0 en el punto P ( 2 , 0 ).
7 ) Halla la ecuación de la tangente a la circunferencia x2 + y2 = 1 desde el punto P(-5, 0) .
Ejercicios de circunferencias I
1 ) Halla la potencia de los puntos A( -2 , 1 ) , B( 0 , 8 ) , D( 1 , -2 ) respecto de la circunferencia C : x² + y²- 8y = 0 . De acuerdo con sus resultados decide su posición relativa.
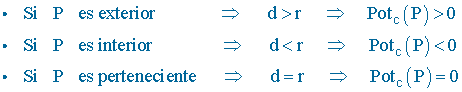

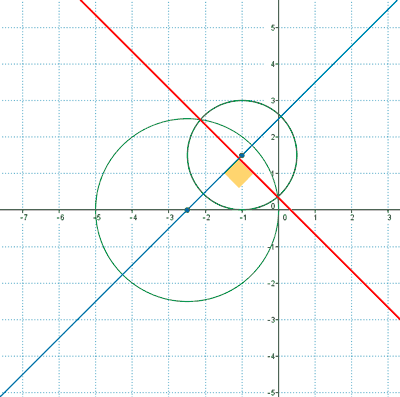
2 ) Halla el eje radical de las siguientes circunferencias.
a ) C1 : x² + y ² + 2x - 3y + 1 = 0
b ) C2 : x² + y ² + 5x = 0
Comprueba que es una recta perpendicular a la línea de sus centros.
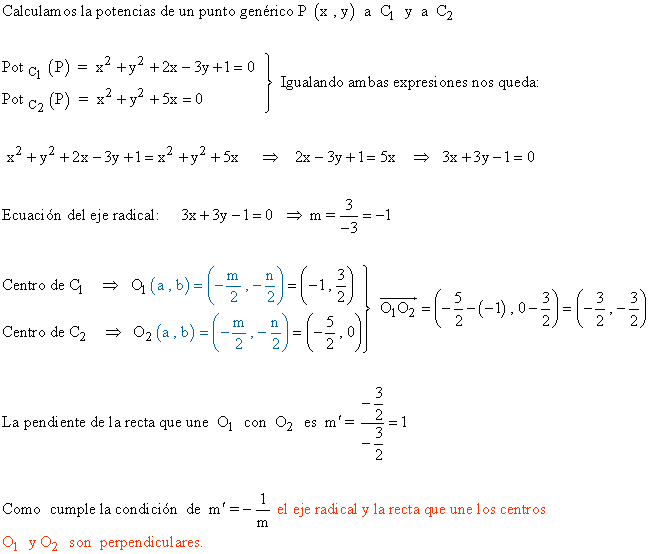
3 ) Halla el eje radical de las siguientes circunferencias.
a ) C1 : x² + y ² - 8x = 0
b ) C2 : 2x² + 2y² - 6x - 16y - 20 = 0
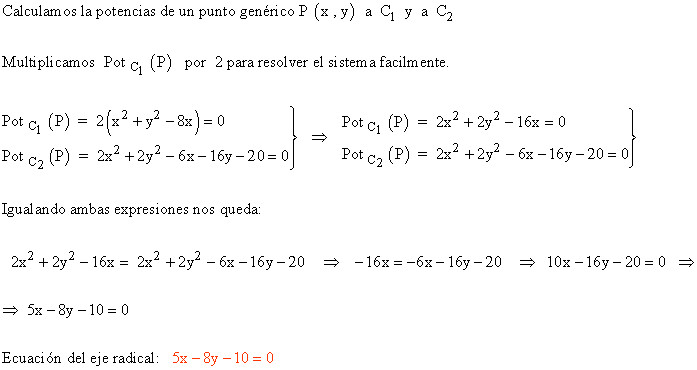
4 ) Halal los ejes radicales y el centro radical de las circunferencias:
C1: x2 + y2 - 4x - 2y - 4 = 0
C2: x2 + y2 - 14x - 8y + 49 = 0
C3: x2 + y2 - 14x + 4y + 37 = 0
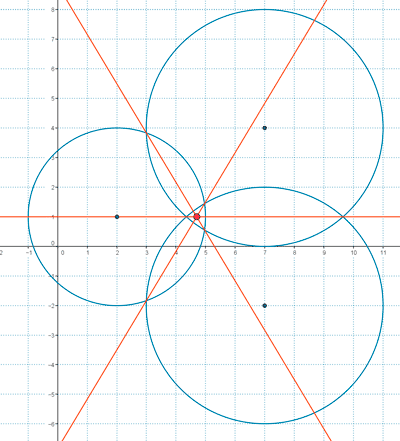
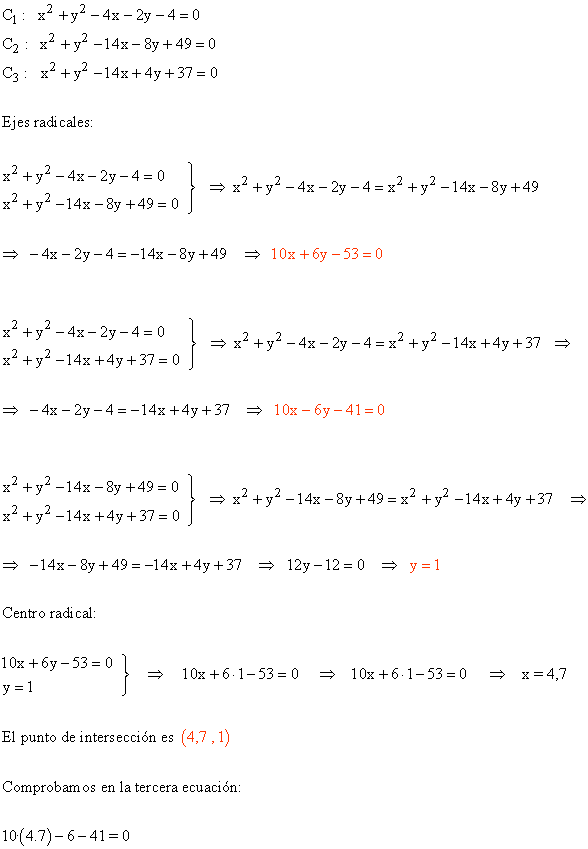
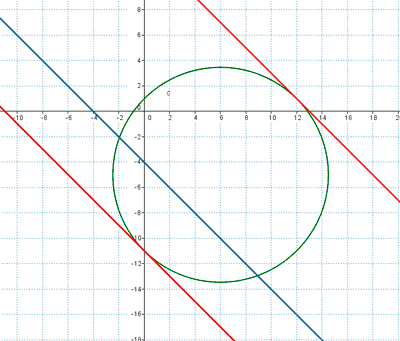
5 ) Dada la circunferencia de ecuación x2 + y2 - 12x + 10y - 11 = 0 , Calcular las rectas tangentes a ella que son paralelas a la recta x + y + 4 = 0 .

6 ) Hallar las ecuaciones de las rectas tangente y normal a la circunferencia x2 + y2 - 10x - 4 y + 16 = 0 en el punto P ( 2 , 0 ).
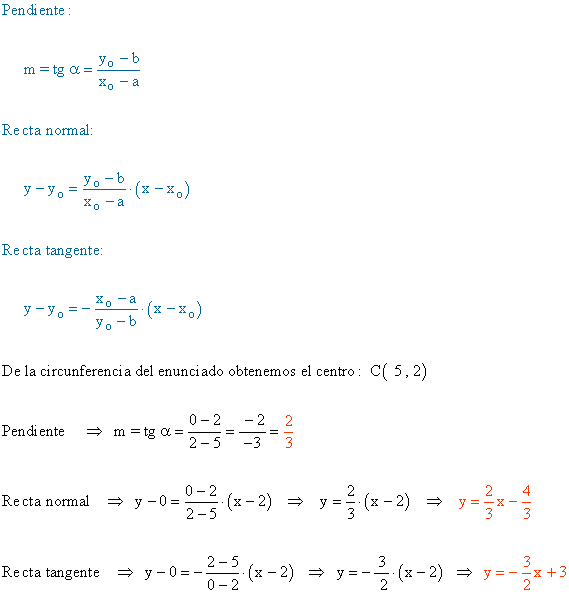
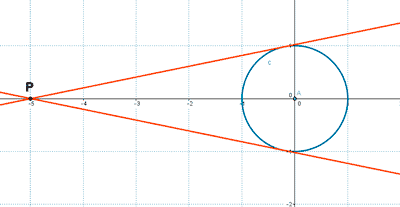
7 ) Halla la ecuación de la tangente a la circunferencia x2 + y2 = 1 desde el punto P(-5, 0) .
Tenemos que resolver el siguiente sistema:
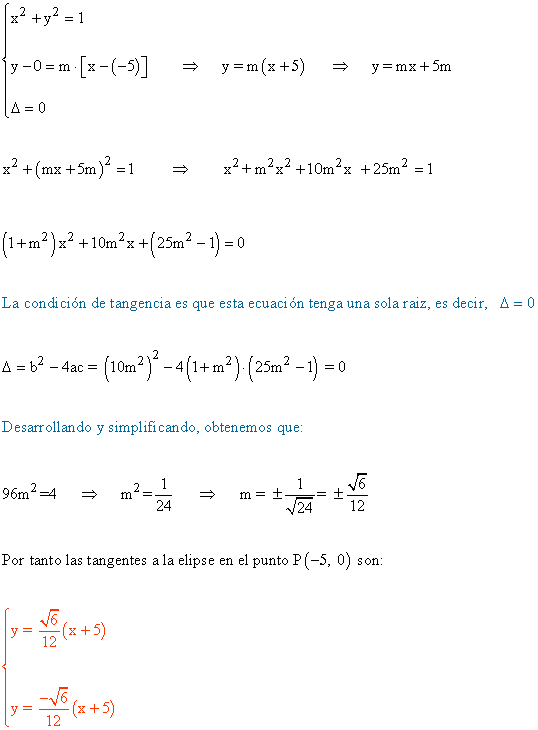


 INICIO
INICIO