Ecuaciones con números complejos:
Teorema fundamental del álgebra
Teorema fundamental del álgebra:
Toda ecuación algebráica de grado n con coeficientes reales o complejos:
![]()
tiene n raíces o soluciones en el conjunto de los números complejos.
Ejemplos:
1) Resuelve la siguiente ecuación: z6 - 1 = 0
Hallar las raíces sextas de la unidad, representarlas gráficamente y expresarlas en forma binómica.
Resolviendo la ecuación en el conjunto de los números reales obtenemos dos soluciones:
![]()
Para obtener las seis raíces o soluciones en el conjunto de los números complejos:
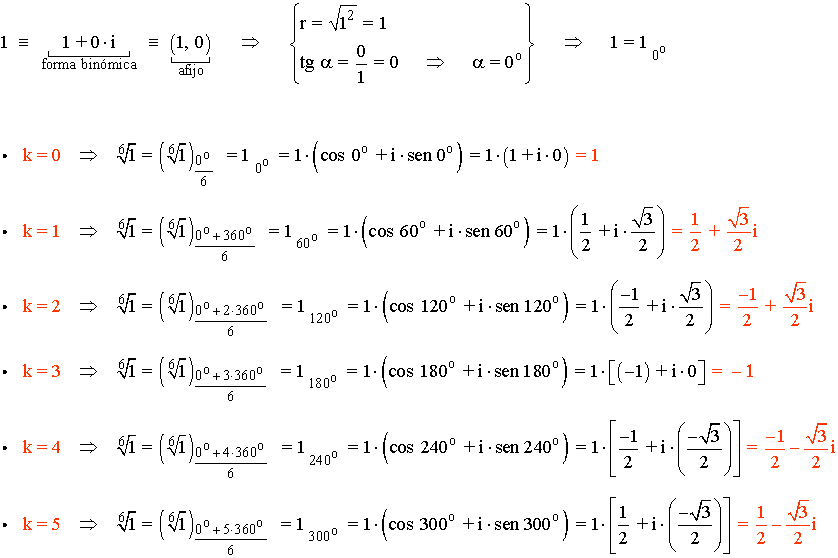
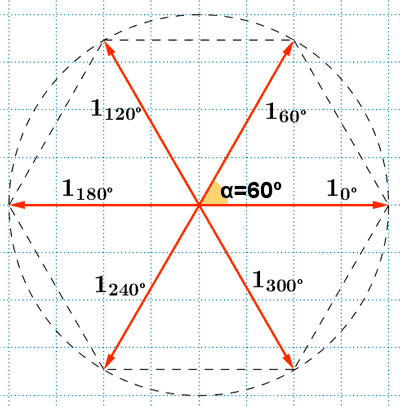
Por lo tanto, las raíces sextas de la unidad son:
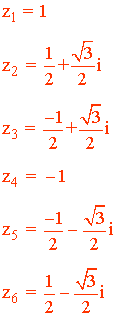
2) Resuelve la siguiente ecuación: z4 - 81 = 0
Resolviendo la ecuación en el conjunto de los números reales obtenemos dos soluciones:
![]()
Para obtener las cuatro raíces o soluciones en el conjunto de los números complejos:
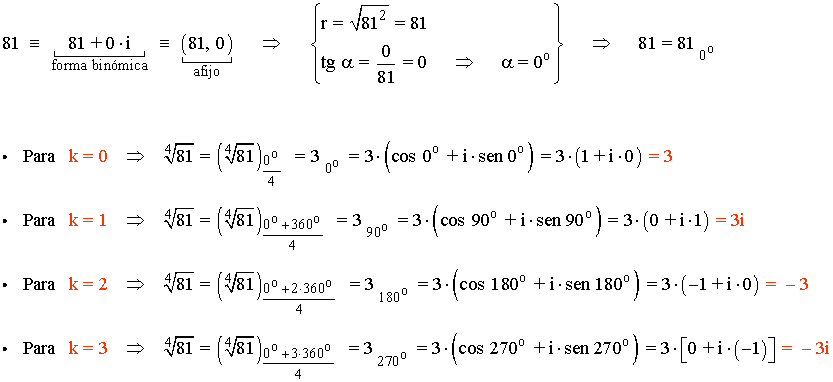
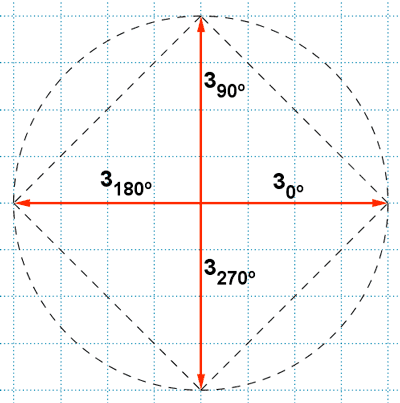
Por lo tanto, las cuatro raíces de la ecuación son:
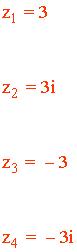
3) Resuelve la siguiente ecuación: z3+ 8 i = 0
Despejando la incógnita z obtenemos que:
![]()
Utilizando la radicación de complejos en forma polar, calculamos las tres raíces de -8 i
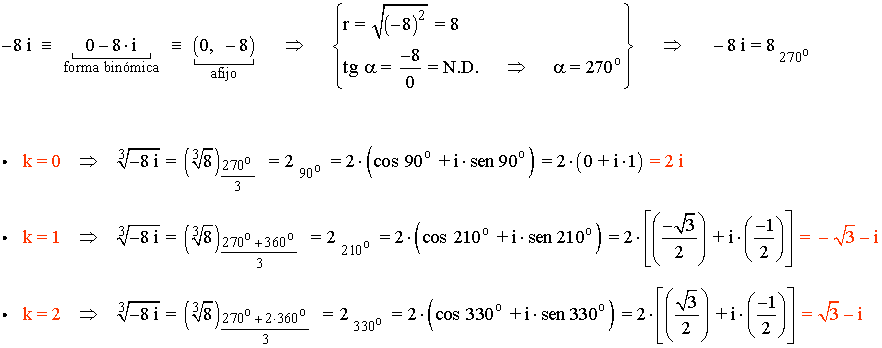
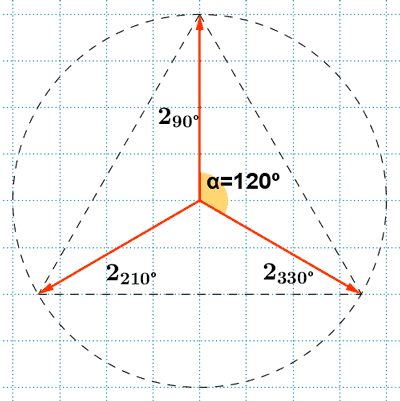
Por lo tanto, las tres raíces de la ecuación son:
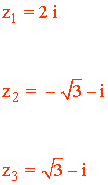


 INICIO
INICIO

