Fórmulas de distribuciones binomial y normal
Distribuciones discretas
Función de probabilidad
Aplicación que asocia a cada valor de la variable aleatoria su probabilidad.
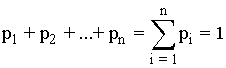
Función de distribución
Asocia a cada valor de la variable la probabilidad acumulada hasta ese valor.
![]()
Parámetros de una variable discreta
| Variable aleatoria X, que toma valores x1, ..., xi, ... , x n | Media aritmética o esperanza: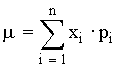 |
Varianza: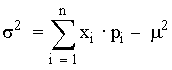 |
Desviación típica: |
|---|
Distribución binomial B(n, p)
- Sólo son posibles dos resultados: éxito y fracaso.
- El resultado de cada prueba es independiente de la anterior.

Función de probabilidad
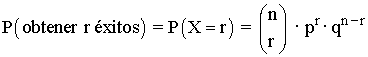
Función de distribución
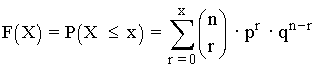
Parámetros
| Media o esperanza matemática | |
|---|---|
| Varianza | |
| Desviación típica |
Distribuciones continuas
Función de densidad
a) f(x) ≥ 0 , para todo x de la variable.
b) El área comprendida entre el eje X y la función f(x) es 1
Función de distribución
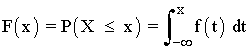
Parámetros
| Variable aleatoria X, que toma valores continuos | Media aritmética o esperanza: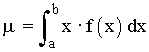 |
Varianza: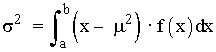 |
Desviación típica: |
|---|
Distribución normal N(μ, σ)
1) La variable toma valores en toda la recta real
2) Su función de densidad es:
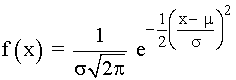
μ es la media y σ la desviación típica.
Distribución normal estándar N(0, 1)
1) La variable toma valores en toda la recta real y se representa con z.
2) Su función de densidad es:
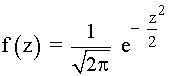
La función de distribución tiene la expresión:
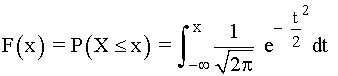
Tipificación de la variable
La transformación de la variable X, que sigue la distribución normal N(μ, σ) que sigue la distribución estándar N(0, 1) recibe el nombre de tipificación de la variable.
![]()
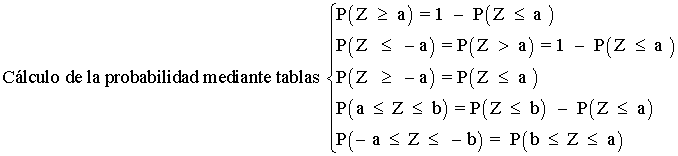
Aproximación de la binomial a la normal

Condiciones de aplicabilidad del teorema de Moivre
![]()
Corrección de continuidad o de Yates
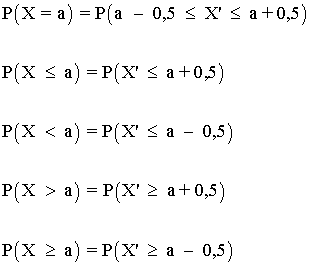


 INICIO
INICIO

