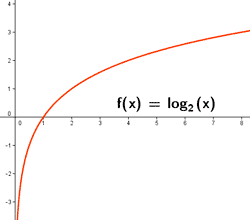
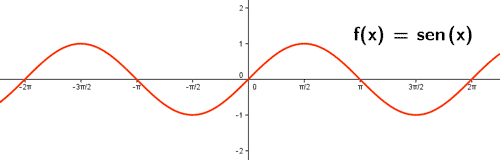
Funciones reales de variable real
Una funcion real f de variable real es una relación que asocia cada número real x un único número real f(x).
Se expresa de la siguiente manera:
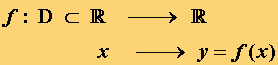
La variable x se llama variable independiente y la variable y es la variable dependiente.
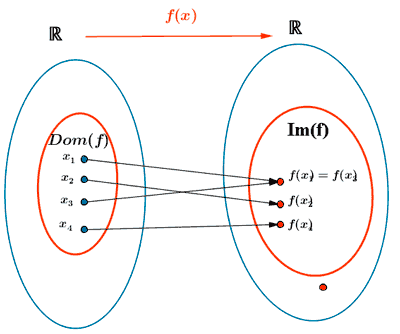
Es función
A cada valor de x le corresponde
un único valor de y
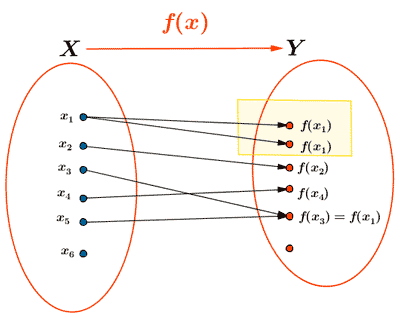
No es función
Al valor x1 le corresponde
dos valores de y
Criterio de la recta vertical para determinar una función
En una gráfica corresponde a una función y = f(x) , ninguna recta vertical la debe cortar en más de un punto.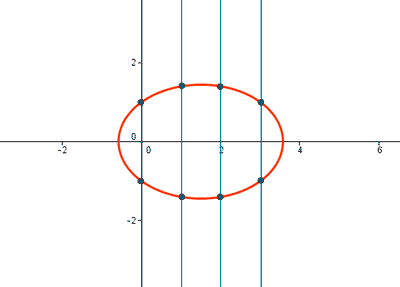
No es función
Si trazamos una recta para cada valor de x ,
ésta corta la función en dos puntos distintos de y
Por ejemplo: si trazamos la recta x = 0 ,
ésta corta la función en los puntos: y = 1 , y = -1
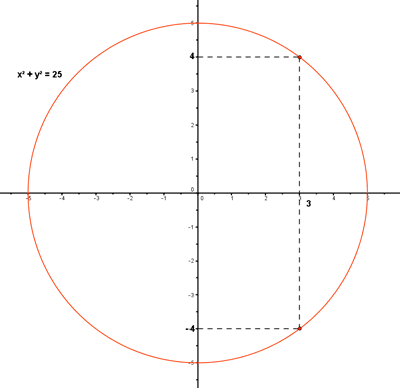
No es función
Hay valores de x a los que
les corresponden dos valores de y
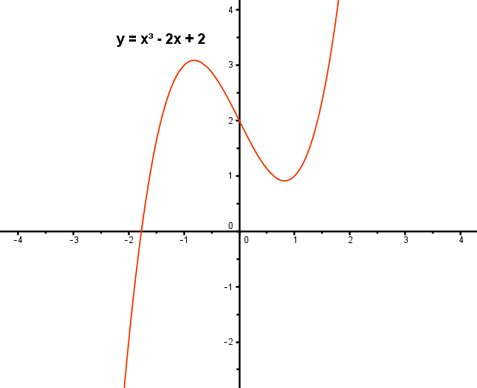
Es función
A cada valor de x le corresponde
un único valor de y
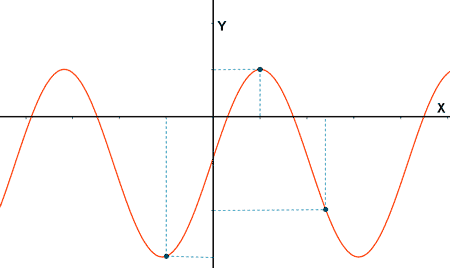
Es función
A cada valor de x le corresponde
un único valor de y
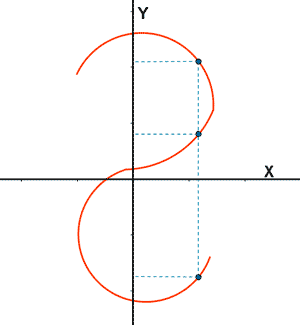
No es función
Hay valores de x a los que
le corresponden 3 valores de y
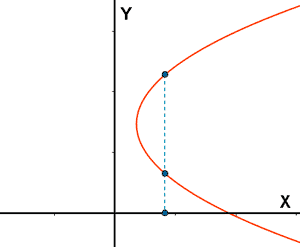
No es función
Hay valores de x a los que
le corresponden 2 valores de y
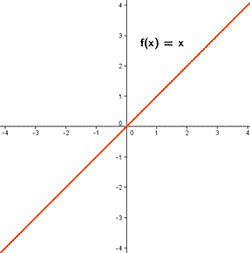
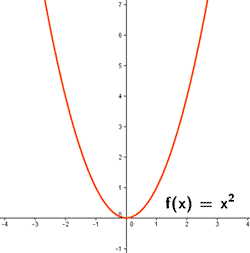
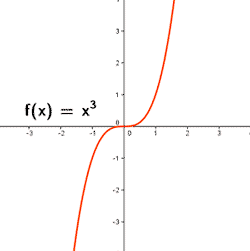
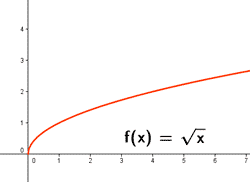
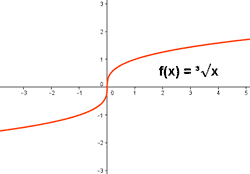
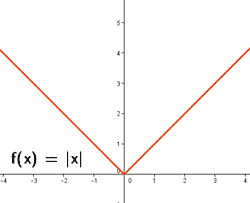
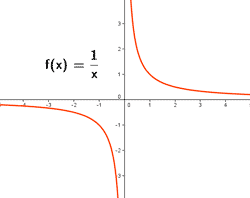
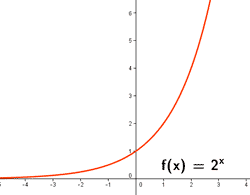
Ejemplos de funciones de variable real:
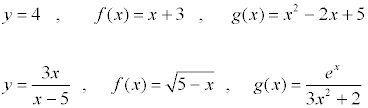
Gráfica de una función
La gráfica de una función está formada por todos los puntos (x , f(x)) , donde x pertenece al dominio de f.


 INICIO
INICIO