Funciones con radicales o funciones irracionales
Las funciones con radicales son las funciones que tienen la variable independiente x bajo el signo radical, es decir:
![]()
Las características generales de las funciones con radicales son:
1) Si n es un número par su dominio es el intervalo en el que g(x) ≥ 0 .
2) Si n es impar, su dominio es R.
3) Su representación gráfica es una rama de una parábola.
1) Ejemplo de función irracional: f(x) = √x
1) Dominio:
Como n es par, el dominio de f(x) es el conjunto de valores donde x ≥ 0 , es decir, Dom(f) = [0, +∞)
2) Puntos de corte:
f(0) = √0 = 0 , es decir, el punto de corte coincide con el eje de coordenadas (0, 0).
3) Tabla de valores:
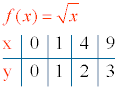
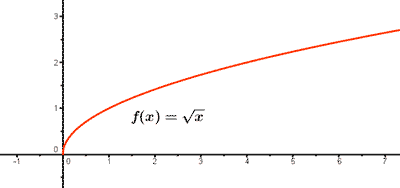
2) Ejemplo de función irracional: f(x) = - √x
1) Dominio:
Como n es par, el dominio de f(x) es el conjunto de valores donde x ≥ 0 , es decir, Dom(f) = [0, +∞)
2) Puntos de corte:
f(0) = - √0 = 0 , es decir, el punto de corte coincide con el eje de coordenadas (0, 0).
3) Tabla de valores:
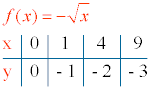
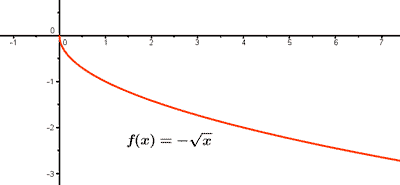
3) Ejemplo de función irracional:
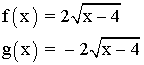
1) Dominio :
El dominio de f (x) y g(x) es el conjunto de valores donde x - 4 ≥ 0, es decir, x ≥ 4. Dom (f) = [ 4, + ∞ ) y Dom (g) = [ 4, + ∞ ).
2) Puntos de corte :
x = 0 no pertenece al dominio de las funciones, por lo que no cortan al eje y.
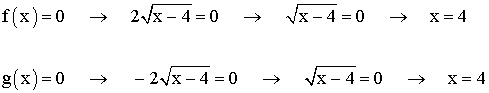
El punto de corte de ambas funciones con el eje x es el punto ( 4, 0 )
3)Tabla de valores :
f (x) :
| x | 4 | 5 | 8 | 13 |
|---|---|---|---|---|
| y | 0 | 2 | 4 | 6 |
g (x) :
| x | 4 | 5 | 8 | 13 |
|---|---|---|---|---|
| y | 0 | - 2 | - 4 | - 6 |
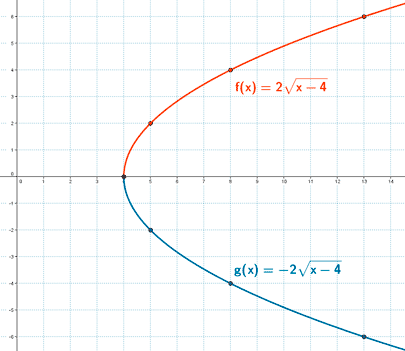
Ejemplo 4 :

1) Dominio :
El dominio de f (x) y de g (x) es el conjunto de valores donde -x + 4 ≥ 0, es decir, - x ≥ -4 → x ≤ 4. Dom (f) = [ - ∞ , 4 ) y Dom (g) = [ - ∞ , 4 )
2) Puntos de corte :
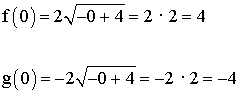
Punto de corte de f (x) con el eje x : ( 0, 4 ) y de g (x) con el eje x es el punto ( 0, - 4
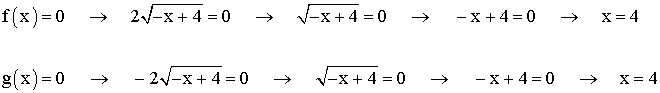
El punto de corte de ambas funciones con el eje x es el punto ( 4, 0 )
3)Tabla de valores :
f (x) :
| x | - 5 | 0 | 3 | 4 |
|---|---|---|---|---|
| y | 6 | 4 | 2 | 0 |
g (x) :
| x | - 5 | 0 | 3 | 4 |
|---|---|---|---|---|
| y | - 6 | - 4 | - 2 | 0 |
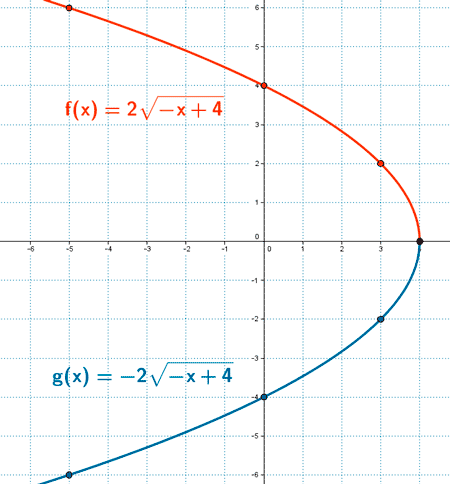
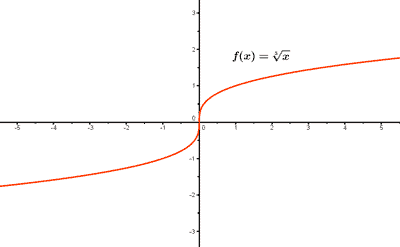
5) Ejemplo de función irracional: f(x) = 3√x
1) Dominio:
Como n es impar, el dominio de f(x) es el conjunto de todos los números reales , es decir, Dom(f) = R .
2) Puntos de corte:
f(0) = 3√0 = 0 , es decir, el punto de corte coincide con el eje de coordenadas (0, 0).
3) Tabla de valores:
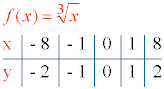


 INICIO
INICIO

