Función polinómica de primer grado o función afín
Las funciones polinómicas de primer grado se llaman funciones afines y son del tipo:
![]()
donde m es la pendiente de la recta y n es la ordenada en el origen.
Las características generales de las funciones polinómicas de primer grado son:
1) Su dominio es el conjunto de los números reales (R).
2) Su gráfica es una recta con pendiente m .
3) Corta el eje X en el punto (0, n) .
4) Si m > 0 la función es creciente.
5) Si m < 0 la función es decreciente.
6) No es simétrica ni periódica.
7) No está acotada.
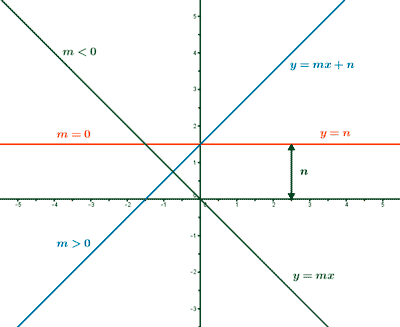
Ejemplo de función afín:
Las funciones afines son rectas oblicuas definidas por dos puntos.
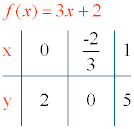
Función creciente (m > 0)
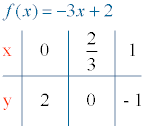
Función decreciente (m < 0)
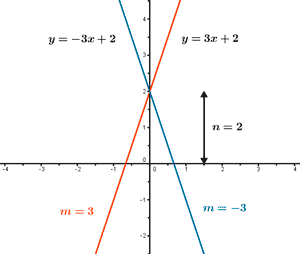
Tipos de funciones afines
Función constante
Si m = 0 la función y = n se denomina función constante y su gráfica es una recta paralela al eje X que pasa por el punto (0, n) .
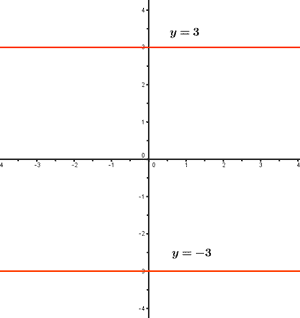
Las funciones y = 3 e y = - 3 son funciones constantes.
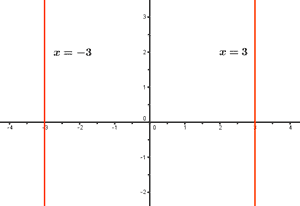
x = k es una recta paralela al eje Y.
No es función puesto que para un valor
determinado existen infinitas imágenes.
Función lineal
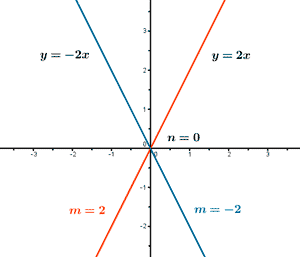
La función y = mx se denomina función lineal y su gráfica es una recta de pendiente m que pasa por el origen de coordenadas: n = 0 .
La función lineal también se llama función de proporcionalidad directa.
y = mx o y = kx , donde el valor de la constante k indica la razón de proporcionalidad.
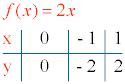
Función creciente (m > 0)
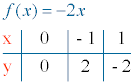
Función decreciente (m < 0)
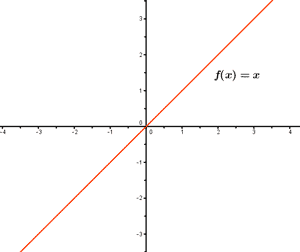
Función identidad: f(x) = x
La función y = x se denomina función identidad que pasa por el origen de coordenadas: n = 0 . Es la recta bisectriz del primer y tercer cuadrante tiene de pendiente m=1 por tanto forma un ángulo de 45º con el eje de abcisas
m = tg α = 1 α = arctg 1 = 45º = π/2
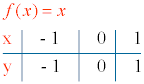


 INICIO
INICIO

