Problemas resueltos de cálculo de probabilidades operando con sucesos
1) De los sucesos A y B se sabe que: 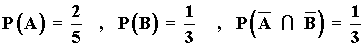 .
.
Halla P(A ∪ B) y P(A ∩ B).
2) Sabiendo que: 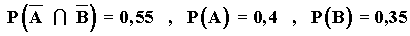
¿son independientes A y B?
3) Calcula la probabilidad P( A ∪ B ) y P( A ∩ B ), sabiendo que P(A ∪ B) - P(A ∩ B) = 0,4 , que P(A) = 0,6 y que P(B) = 0,8 .
4) Sean A y B dos sucesos tales que : 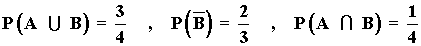
Halla P(B) , P(A) y 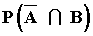 y la probabilidad condicionada P(A/B)
y la probabilidad condicionada P(A/B)
5-A) Se sabe que dado el suceso A, la probabilidad de que suceda B es de 0,3, es decir, que P(B/A) = 0,3 . ¿Cuánto vale la probabilidad de que dado A, no ocurra B?
5-B) Calcula la probabilidad del suceso 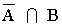 sabiendo que la probabilidad de que ocurra al menos uno de los dos sucesos A o B es 0,8 y que P(A) = 0,3.
sabiendo que la probabilidad de que ocurra al menos uno de los dos sucesos A o B es 0,8 y que P(A) = 0,3.
6) Sean A y B dos sucesos aleatorios tales que P(A) = 0,4 , P(B) = 0,7 y P(A/B) = 0,6
Calcula estas probabilidades:
a) P(A ∩ B) b) P(A ∪ B) c) P(B/A) d) 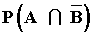 e)
e) 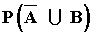 f)
f) 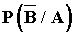
7) Sean A y B dos sucesos con P(A) = 0,5 , P(B) = 0,3 y P(A ∩ B) = 0,1 . Calcula las siguientes probabilidades.
a) P(A ∪ B) b) P(A/B) c) P(A/A ∩ B) d) P(A/A ∪ B)
8) Sean A y B dos sucesos de un espacio de probabilidad, de manera que P(A) = 0,4 , P(B) = 0,3 y P(A ∩ B) = 0,1 . Calcula razonadamente:
a) P(A ∪ B) b) 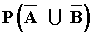 c) P(A/B) d)
c) P(A/B) d) 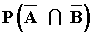
9) 
10) En un espacio probabilístico se consideran los sucesos A y B, cuyas probabilidades son P(A) = 0,4 , P(B) = 0,3 y P(A ∪ B) = 0,5. Calcular razonadamente las probabilidades P(A ∩ B) y P(A/B), siendo A/B el suceso A condicionado a B. Justificar si los sucesos A y B son o no independientes.
11) Dados dos sucesos independientes A y B, la probabilidad de que ocurran los dos a la vez es de 1/6 y de que no ocurra ninguno de los dos 1/3 . Calcula sus probabilidades.
12) Se sabe que P(B/A) = 0,9 , P(A/B) = 0,2 y P(A) = 0,1
a) Calcula P(A ∩ B) y P(B)
b) ¿Son independientes los sucesos A y B? ¿Por qué?
c) Calcula 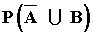
13) Al 20% de los alumnos de bachillerato le gusta un grupo musical A, mientras que al 80% restante no le gusta este grupo. En cambio otro grupo musical B gusta a la mitad y no a la otra mitad. Hay un 30% de alumnos de bachillerato al que no gusta ninguno de los dos grupos. Si se elige un estudiante de bachillerato al azar:
a) ¿Cuál es la probabilidad de que le gusten los dos grupos?
b) ¿Cuál es la probabilidad de que le guste alguno de los dos grupos?
c) ¿Cuál es la probabilidad de que le guste el grupo B y no el grupo A?
14) Cierto estudio de mercado revela que el 50% de los entrevistados consume el producto A, el 40% consume el B y el 25% no consume ninguno de ellos. Si seleccionamos al azar un individuo de los entrevistados, expresa los siguientes sucesos en función de los sucesos simples A = "consumir A" , B = "consumir B" y calcula su probabilidad:
a) Que consuma los dos productos.
b) Que sólo consuma uno de los productos.
c) Si sabemos que consume el producto A, que consuma también el B.
15) Dados dos sucesos A y B, sabemos que P(A ∩ B) = 0,1 , P(A ∪ B) = 0,7 y P(A/B) = 0,2
a) Calcula P(A) y P(B)
b) ¿Son independientes los sucesos A y B? ¿Por qué?
c) Calcula 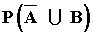
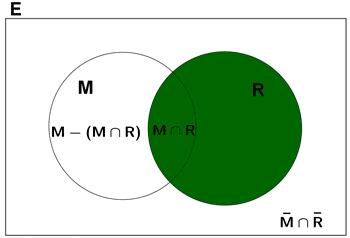
16) Un estudio revela que el 10% de los oyentes de radio sintoniza a diario las cadenas Music y Rhythm , que un 35% sintoniza a diario Music y que el 55% de los oyentes no escucha ninguna de las dos emisoras. Obtén:
a) La probabilidad de que un oyente elegido al azar sintonice la cadena Rhythm.
b) La probabilidad de que un oyente elegido al azar sintonice la cadena Rhythm pero no la Music.
c) La probabilidad de que un oyente, del que sabemos que escucha Rhythm, escuche Music.
17) Al 80% de los miembros de una sociedad gastronómica le gusta el vino Ramïm Negre. Entre estos, al 75% le gusta el queso de cabra. Además, a un 4% de los miembros de esta sociedad no le gusta el vino Raïm Negre ni el queso de cabra.
a) ¿A qué porcentaje le gusta tanto el vino Raïm Negre como el queso de cabra?
b) ¿A qué porcentaje no le gusta el queso de cabra?
c) Si a un miembro de la sociedad le gusta el queso de cabra, ¿cuál es la probabilidad de que le guste el vino Raïm Negre?
d) ¿A qué porcentaje le gusta el vino Raïm Negre entre aquellos a los que no les gusta el queso de cabra?
18) Un sistema está formado por dos componentes A y B. El sistema funciona si funciona alguna de sus componentes, la probabilidad de que funcione A es P(A) = 0,8, la de que funcione B es P(B) = 0,7, y 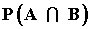 = 0,6.
= 0,6.
a) ¿Cuál es la probabilidad de que el sistema funcione?
b) ¿Cuál es la probabilidad de que funcione la componente A, sabiendo que la componente B no funciona?
1) De los sucesos A y B se sabe que 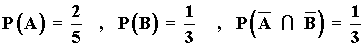 .
.
Halla P(A ∪ B) y P(A ∩ B).
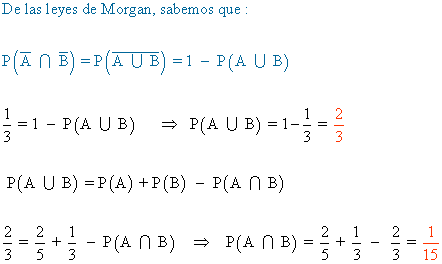
2) Sabiendo que 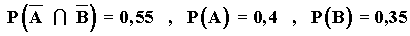
¿son independientes A y B?

3) Calcula la probabilidad P(A ∪ B) y P(A ∩ B), sabiendo que P(A ∪ B) - P(A ∩ B) = 0,4 , que P(A) = 0,6 y que P(B) = 0,8 .

4) Sean A y B dos sucesos tales que : 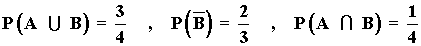
Halla P(B) , P(A) y 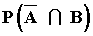 y la probabilidad condicionada P(A/B)
y la probabilidad condicionada P(A/B)
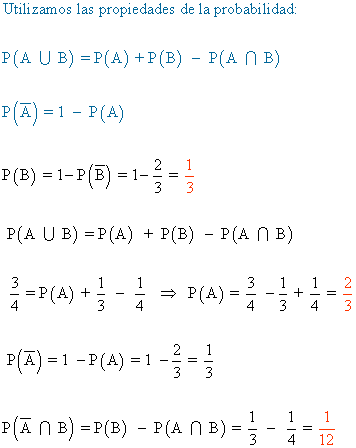
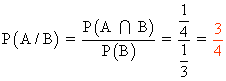
5-A) Se sabe que dado el suceso A, la probabilidad de que suceda B es de 0,3, es decir, que P(B/A) = 0,3 . ¿Cuánto vale la probabilidad de que dado A, no ocurra B?
![]()
5-B) Calcula la probabilidad del suceso 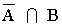 sabiendo que la probabilidad de que ocurra al menos uno de los dos sucesos A o B es 0,8 y que P(A) = 0,3.
sabiendo que la probabilidad de que ocurra al menos uno de los dos sucesos A o B es 0,8 y que P(A) = 0,3.
![]()
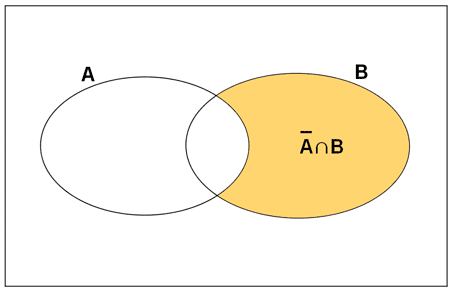
6) Sean A y B dos sucesos aleatorios tales que P(A) = 0,5 , P(B) = 0,7 y P(A/B) = 0,6
Calcula estas probabilidades:
a) P(A ∩ B) b) P(A ∪ B) c) P(B/A) d) 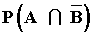 e)
e) 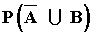 f)
f) 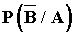

7) Sean A y B dos sucesos con P(A) = 0,5 , P(B) = 0,3 y P(A ∩ B) = 0,1 . Calcula las siguientes probabilidades.
a) P(A ∪ B) b) P(A/B) c) P(A/A ∩ B) d) P(A/A ∪ B)
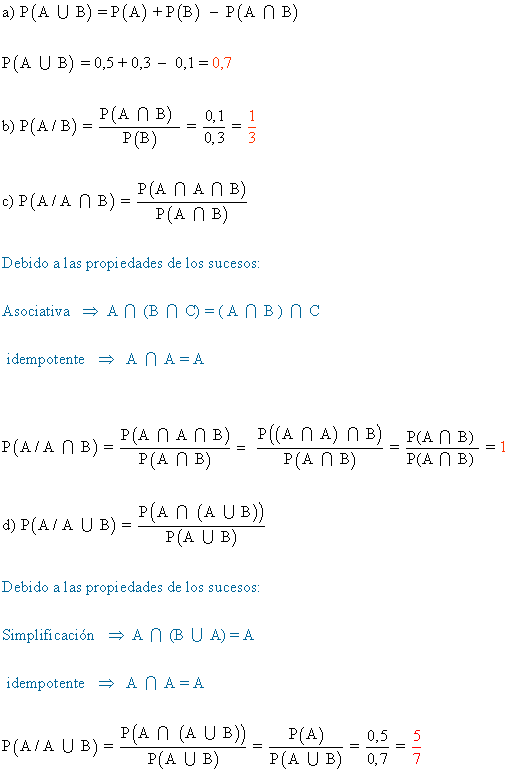
8) Sean A y B dos sucesos de un espacio de probabilidad, de manera que P(A) = 0,4 , P(B) = 0,3 y P(A ∩ B) = 0,1 . Calcula razonadamente:
a) P(A ∪ B) b) 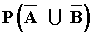 c) P( A/B ) d)
c) P( A/B ) d) 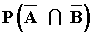
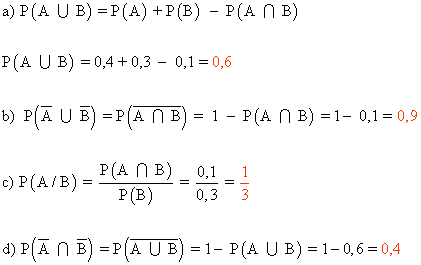
9) 


10) En un espacio probabilístico se consideran los sucesos A y B, cuyas probabilidades son P(A) = 0,4 , P(B) = 0,3 y P(A ∪ B) = 0,5. Calcular razonadamente las probabilidades P(A ∩ B) y P(A/B), siendo A/B el suceso A condicionado a B. Justificar si los sucesos A y B son o no independientes.

11) Dados dos sucesos independientes A y B, la probabilidad de que ocurran los dos a la vez es de 1/6 y de que no ocurra ninguno de los dos 1/3 . Calcula sus probabilidades.

12) Se sabe que P(B/A) = 0,9 , P(A/B) = 0,2 y P(A) = 0,1
a) Calcula P(A ∩ B) y P(B)
b) ¿Son independientes los sucesos A y B? ¿Por qué?
c) Calcula 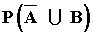
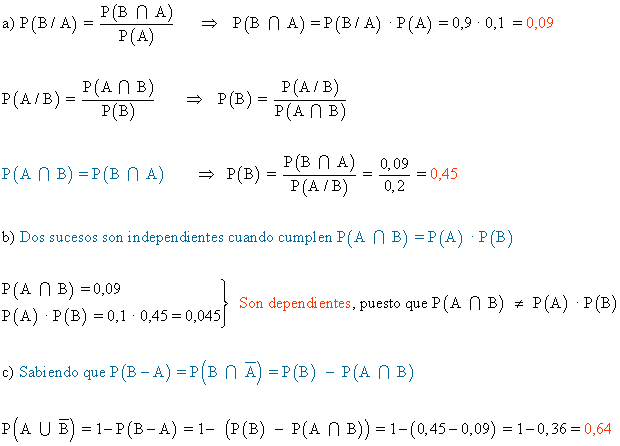
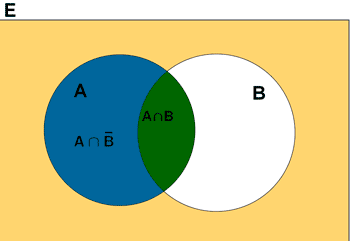
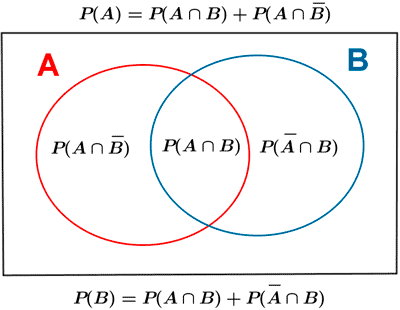
El resultado es todo lo que está coloreado.
13) Al 20% de los alumnos de bachillerato le gusta un grupo musical A, mientras que al 80% restante no le gusta este grupo. En cambio otro grupo musical B gusta a la mitad y no a la otra mitad. Hay un 30% de alumnos de bachillerato al que no gusta ninguno de los dos grupos. Si se elige un estudiante de bachillerato al azar:
a) ¿Cuál es la probabilidad de que le gusten los dos grupos?
b) ¿Cuál es la probabilidad de que le guste alguno de los dos grupos?
c) ¿Cuál es la probabilidad de que le guste el grupo B y no el grupo A?
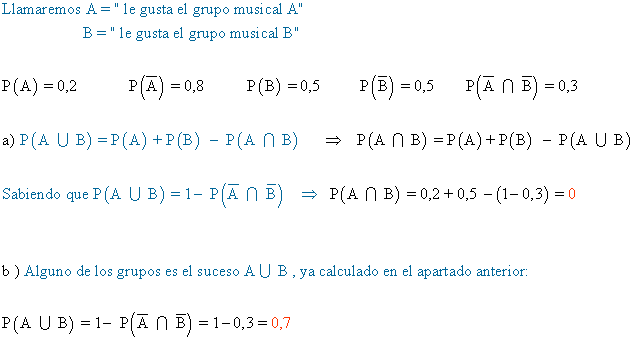
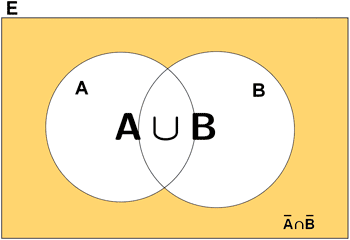
El resultado es todo lo que no está coloreado.
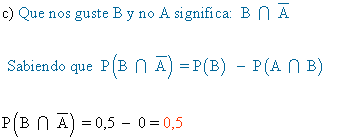
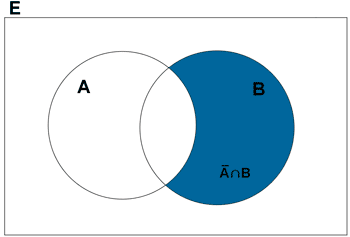
El resultado es todo lo que está coloreado.
14) Cierto estudio de mercado revela que el 50% de los entrevistados consume el producto A, el 40% consume el B y el 25% no consume ninguno de ellos. Si seleccionamos al azar un individuo de los entrevistados, expresa los siguientes sucesos en función de los sucesos simples A = "consumir A" , B = "consumir B" y calcula su probabilidad:
a) Que consuma los dos productos.
b) Que sólo consuma uno de los productos.
c) Si sabemos que consume el producto A, que consuma también el B.
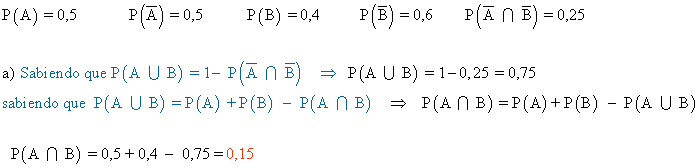

El resultado es todo lo que no está coloreado.


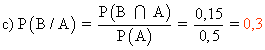
15) Dados dos sucesos A y B, sabemos que P(A ∩ B) = 0,1 , P(A ∪ B) = 0,7 y P(A/B) = 0,2
a) Calcula P(A) y P(B)
b) ¿Son independientes los sucesos A y B? ¿Por qué?
c) Calcula 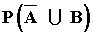

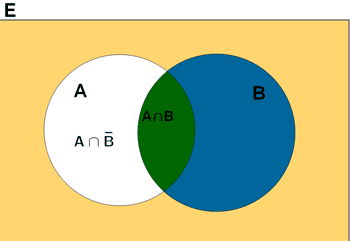
El resultado es todo lo que está coloreado.
16) Un estudio revela que el 10% de los oyentes de radio sintoniza a diario las cadenas Music y Rhythm , que un 35% sintoniza a diario Music y que el 55% de los oyentes no escucha ninguna de las dos emisoras. Obtén:
a) La probabilidad de que un oyente elegido al azar sintonice la cadena Rhythm.
b) La probabilidad de que un oyente elegido al azar sintonice la cadena Rhythm pero no la Music.
c) La probabilidad de que un oyente, del que sabemos que escucha Rhythm, escuche Music.


17) Al 80% de los miembros de una sociedad gastronómica le gusta el vino Ramïm Negre. Entre estos, al 75% le gusta el queso de cabra. Además, a un 4% de los miembros de esta sociedad no le gusta el vino Raïm Negre ni el queso de cabra.
a) ¿A qué porcentaje le gusta tanto el vino Raïm Negre como el queso de cabra?
b) ¿A qué porcentaje no le gusta el queso de cabra?
c) Si a un miembro de la sociedad le gusta el queso de cabra, ¿cuál es la probabilidad de que le guste el vino Raïm Negre?
d) ¿A qué porcentaje le gusta el vino Raïm Negre entre aquellos a los que no les gusta el queso de cabra?
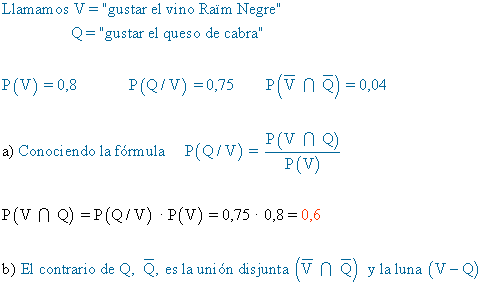
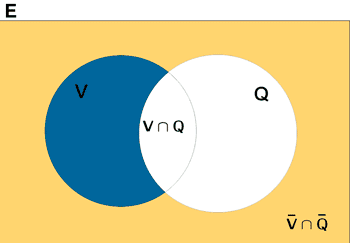
El resultado es todo lo que está coloreado.
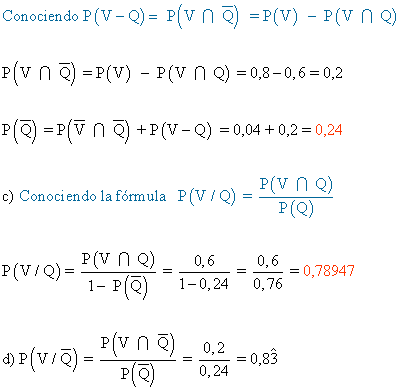
18) Un sistema está formado por dos componentes A y B. El sistema funciona si funciona alguna de sus componentes, la probabilidad de que funcione A es P(A) = 0,8, la de que funcione B es P(B) = 0,7, y 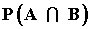 = 0,6.
= 0,6.
a) ¿Cuál es la probabilidad de que el sistema funcione?
b) ¿Cuál es la probabilidad de que funcione la componente A, sabiendo que la componente B no funciona?



 INICIO
INICIO