Diagrama de árbol y tablas de contingencia en experimentos compuestos
Diagramas de árbol
En un diagrama de árbol cada posible resultado del experimento compuesto será una secuencia que contiene los resultados de cada uno de los experimentos simples que lo componen.
Ejemplo 1 :
Consideremos el experimento aleatorio de lanzar una moneda y un dado cúbico,
con sus caras
numeradas del 1 al 6. Hallar la probabilidad de :
a) Obtener cara y salir cuatro.
b) Obtener cruz y un número mayor que cinco.
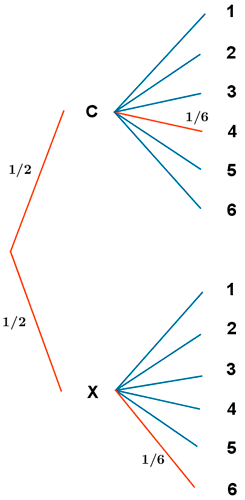
a)
Basándonos en el diagrama de árbol :
P ( C, 4 ) = 1 / 2 · 1 / 6 = 1 / 12
b)
P ( X, mayor que 5 ) = 1 / 2 · 1 / 6 = 1 / 12
Tablas de contingencia
Para calcular probabilidades de sucesos compuestos se pueden organizar los datos en una tabla de doble entrada que se llama tabla de contingencia.
| A | Total | ||
|---|---|---|---|
| B | P ( A ∩B ) | P ( B ) | |
| Total | P ( A ) | 1 |
Ejemplo 2:
En 4º de secundaria hay 22 chicos y 18 chicas. Llevan gafas 8 chicos y 6 chicas.
Elegido un alumno al azar, calcula la probabilidad de que sea chico y no lleve gafas.
En primer lugar recogemos los datos de un problema en una tabla de contingencia o de doble entrada.
| Chico | Chica | Total | |
|---|---|---|---|
| Con gafas | 8 | 6 | |
| Sin gafas | |||
| Total | 22 | 18 |
En segundo lugar completamos la tabla.
| Chico | Chica | Total | |
|---|---|---|---|
| Con gafas | 8 | 6 | 14 |
| Sin gafas | 14 | 12 | 26 |
| Total | 22 | 18 | 40 |
En último lugar, se extraen los datos necesarios de la tabla para calcular la probabilidad pedida.
![]()


 INICIO
INICIO

