Problemas resueltos de dependencia e independencia de sucesos.
Probabilidad compuesta.
1) Un producto está formado de dos partes: A y B, que se fabrican independientemente. La probabilidad de un defecto en A es 0,06 y la probabilidad de un defecto en B es 0,07. ¿Cúal es la probabilidad de que el producto no sea defectuoso?
2) En el bachillerato de cierto instituto hay un total de 100 alumnos, de los cuales: 40 son varones, 30 usan gafas, y 15 son varones y usan gafas. Si seleccionamos al azar un alumno de dicho curso:
a) ¿Cuál es la probabilidad de que sea mujer y no use gafas?
b) Si sabemos que el alumno seleccionado no usa gafas, ¿qué probabilidad hay de que sea varón? Justifica las respuestas.
3) En un grupo de familias, un 10 % ha cambiado de coche y también ha camiado de piso. Un 50 % no ha cambiado de coche y sí de piso. Entre los que han cambiado de coche, un 25 % ha cambiado de piso.
a) ¿Qué porcentaje de familias ha cambiado de piso?
b) ¿Qué probabilidad hay de que una familia del grupo haya cambiado de coche?
c) De las familias que no han cambiado de piso, ¿qué porcentaje ha cambiado de coche?
4) Los ciudadanos de una localidad votaron "Sí" o "No" a una determinada propuesta que realizó su Ayuntamiento. Los resultados por porcentajes vienen reflejados en la tabla que mostramos a continuación.
¿Son los sucesos A = { ser varón } y B = { votar Sí } independientes?
Varones
Mujeres
Sí
25 %
35 %
60 %
No
30 %
10 %
40 %
55 %
45 %
| Varones | Mujeres | ||
|---|---|---|---|
| Sí | 25 % | 35 % | 60 % |
| No | 30 % | 10 % | 40 % |
| 55 % | 45 % |
5) De dos tiradores se sabe que uno de ellos hace dos dianas de cada tres disparos, y el otro consigue tres dianas de cada cuatro disparos. Si los dos disparan simultáneamente, halle la probabilidad de que :
a) Ambos acierten. b) Uno acierte y el otro no.
c) Ninguno de los dos acierte. d) Alguno acierte.
6) El 60 % de los alumnos de cierta asignatura aprueba en junio. El 80 % de los presentados en septiembre también aprueba la asignaura. Sabiendo que los alumnos que se presentaros en septiembre son todos los que no aprobaron en junio, determina :
a) La probabilidad de que un alumno seleccionado al azar haya aprobado la asignatura.
b) Si sabemos que un estudiante ha aprobado la asignatura, la probabilidad de que haya sido en junio.
7) El examen de Matemáticas de un alumno consta de dos ejercicios. La probabilidad de que resuelva el primero es del 30 % , la de que resuelva ambos es del 10 % , y la de que no resuelva ninguno es del 35 %. Calcule la probabilidades de los siguiente sucesos :
a) Que el alumno resuelva el segundo ejercicio.
b) Que resuelva el segundo ejercicio, sabiendo que no ha resuelto el primero.
8) Una clase tiene 24 alumnos y todos ellos cursan inglés y matemáticas. La mitad aprueban inglés, 16 aprueban matemáticas, y 4 suspenden inglés y matemáticas.
a) Realiza una tabla de contingencia con los resultados de esta clase.
b) Calcula la probabilidad de que, al elegir un alumno de esta clase al azar, resulte que aprueba matemáticas y suspende inglés.
c) En esta clase, ¿son independientes los sucesos "aprobar inglés" y "aprobar matemáticas" ?
9) Una fábrica produce tornillos niquelados y dorados, siendo el 75 % de los tornillos que produce niqelados. El porcentaje de tornillos defectuosos producidos es del 4 % para los tornillos niquelados y del 5 % para los dorados. Se elige al azar un tornillo y resulta no ser defectuoso. ¿Cuál es la probabilidad de que sea niquelado?
10) En un experimento aleatorio consistente en lanzar simultáneamente tres dados equilibrados de seis caras se pide calcular la probabilidad de obtener :
a) Tres unos.
b) Al menos un dos.
c) Tres números distintos.
d) Una suma de 4.
11) Una caja con una docena de huevos contiene dos de ellos rotos. Se extraen al azar y sin reemplazamiento cuatro huevos. Calcula la probabilidad de extraer :
a) Los cuatro huevos en un buen estado.
b) De entre los cuatro huevos, exactamente uno roto.
12) Se realiza una encuesta sobre la aceptación de dos productos A y B entre la población. El 45 % de la población consume el producto A, el 30 % consume el producto B y el 20 % consume ambos productos. Seleccionado un individuo de esa población al azar, se pide:
a) Si consume el producto A, calcular la probabilidad de que consuma el producto B.
b) Si consume el producto B, calcular la probabilidad de que no consuma el producto A.
c) Calcular la probabilidad de que no consuma ni A ni B.
13) De una baraja de cuarenta cartas se extraen sucesivamente tres cartas al azar. Determina la probabilidad de obtener :
a) Tres reyes.
b) Una figura en la primera carta, un cinco en la segunda y un seis en la tercera.
c) Un as, un tres y un seis en cualquier orden.
14) Un ordenador personal tiene cargados dos programas antivirus A1 y A2 que actúan simultánea e independientemente. Ante la presencia de un virus, el programa A1 lo detecta con una probabilidad de 0,9 y el programa A2 lo detecta con una probabilidad de 0,8. Calcular de forma razonada :
a) La probabilidad de que un virus cualquiera sea detectado.
b) La probabilidad de que un virus sea detectado por el programa A1 y no por A2.
15) Se extraen cuatro cartas de una baraja española. Halla la probabilidad de que las cuatro cartas sean del mismo palo en los siguientes casos :
a) Con devolución de la carta a la baraja.
b) Sin devolución.
16) Tenemos una urna con 3 bolas rojas, 2 bolas verdes y 2 bolas azules.
Vamos a extraer 2 bolas al azar.
Definimos los sucesos R1 = { obtener una bola roja en la primera extracción }
y R2 = { obtener una bola roja en la segunda extracción}
Calcular las probabilidades de los sucesos si hay reemplazamiento de bola y si no hay reemplazamiento de bola.
17) De una urna con 4 bolas azules y 3 bolas rojas, extraemos dos bolas. Calcular la probabilidad de que:
a) Ambas bolas sean azules.
b) La primera bola sea azul y la segunda bola sea roja.
c) Las dos bolas sean rojas.
18) Una urna A contiene 6 bolas blancas y 4 negras. Otra urna B contiene 5 bolas blancas y 9 negras. Elegimos, a cara o cruz, una urna y extraemos dos bolas., que resultan ser blancas. Halla la probabilidad de que la urna elegida haya sido la A.
19) En un almacén hay tres tipos de estanterías en las que hay colocados dos tipos de productos: A y B. En la primera hay 30 de tipo A y 40 de tipo B; en la segunda, 10 de tipo A y 50 de tipo B, y en la tercera, 25 de tipo A y 25 de tipo B.
a) Si elegimos una estantería y un producto al azar, calcula la probabilidad de que este sea del tipo A.
b) Si elegimos un producto al azar de una de las estanterías y resulta que es del tipo B, halla la probabilidad de que proceda de la segunda estantería.
20) La probabilidad de que un chico sea elegido para formar parte de un coro es de 0,42 mientras que la probabilidad de que sea elegida una chica es de 0,55. Entre los aspirantes se elige al azar a un chico y una chica. Halla la probabilidad de que :
a) Los dos formen parte del coro.
b) Ninguno de los dos forme parte del coro.
c) Solo forme parte del coro la chica.
d) Al menos uno forme parte del coro.
1) Un producto está formado de dos partes: A y B, que se fabrican independientemente. La probabilidad de un defecto en A es 0,06 y la probabilidad de un defecto en B es 0,07. ¿Cúal es la probabilidad de que el producto no sea defectuoso?

2) En el bachillerato de cierto instituto hay un total de 100 alumnos, de los cuales: 40 son varones, 30 usan gafas, y 15 son varones y usan gafas. Si seleccionamos al azar un alumno de dicho curso:
a) ¿Cuál es la probabilidad de que sea mujer y no use gafas?
b)Si sabemos que el alumno seleccionado no usa gafas, ¿qué probabilidad hay de que sea varón? Justifica las respuestas.
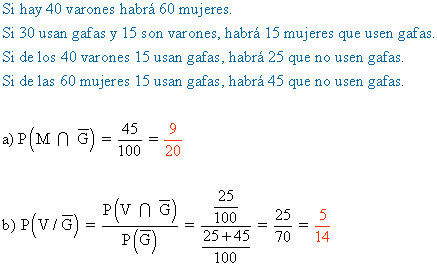
3) En un grupo de familias, un 10 % ha cambiado de coche y también ha camiado de piso. Un 50 % no ha cambiado de coche y sí de piso. Entre los que han cambiado de coche, un 25 % ha cambiado de piso.
a) ¿Qué porcentaje de familias ha cambiado de piso?
b) ¿Qué probabilidad hay de que una familia del grupo haya cambiado de coche?
c) De las familias que no han cambiado de piso, ¿qué porcentaje ha cambiado de coche?
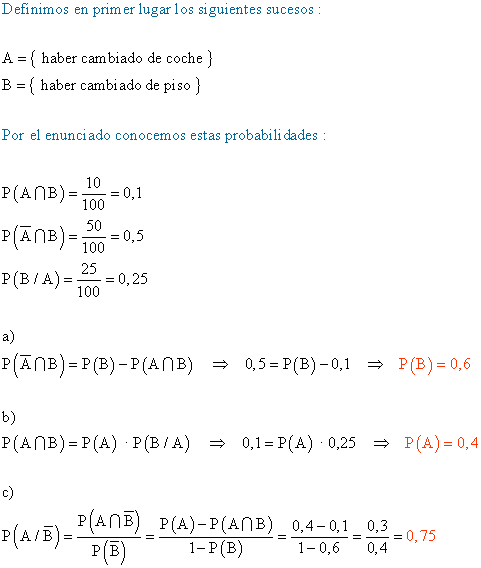
4) Los ciudadanos de una localidad votaron "Sí" o "No" a una determinada propuesta que realizó su Ayuntamiento. Los resultados por porcentajes vienen reflejados en la tabla que mostramos a continuación.
¿Son los sucesos A = { ser varón } y B = { votar Sí } independientes?
Varones
Mujeres
Sí
25 %
35 %
60 %
No
30 %
10 %
40 %
55 %
45 %
| Varones | Mujeres | ||
|---|---|---|---|
| Sí | 25 % | 35 % | 60 % |
| No | 30 % | 10 % | 40 % |
| 55 % | 45 % |

5) De dos tiradores se sabe que uno de ellos hace dos dianaas de cada tres disparos, y el otro consigue tres dianas de cada cuatro disparos. Si los dos disparan simultáneamente, halle la probabilidad de que :
a) Ambos acierten. b) Uno acierte y el otro no.
c) Ninguno de los dos acierte. d) Alguno acierte.

6) El 60 % de los alumnos de cierta asignatura aprueba en junio. El 80 % de los presentados en septiembre también aprueba la asignaura. Sabiendo que los alumnos que se presentaros en septiembre son todos los que no aprobaron en junio, determina :
a) La probabilidad de que un alumno seleccionado al azar haya aprobado la asignatura.
b) Si sabemos que un estudiante ha aprobado la asignatura, la probabilidad de que haya sido en junio.

7) El examen de Matemáticas de un alumno consta de dos ejercicios. La probabilidad de que resuelva el primero es del 30 % , la de que resuelva ambos es del 10 % , y la de que no resuelva ninguno es del 35 %. Calcule la probabilidades de los siguiente sucesos :
a) Que el alumno resuelva el segundo ejercicio.
b) Que resuelva el segundo ejercicio, sabiendo que no ha resuelto el primero.
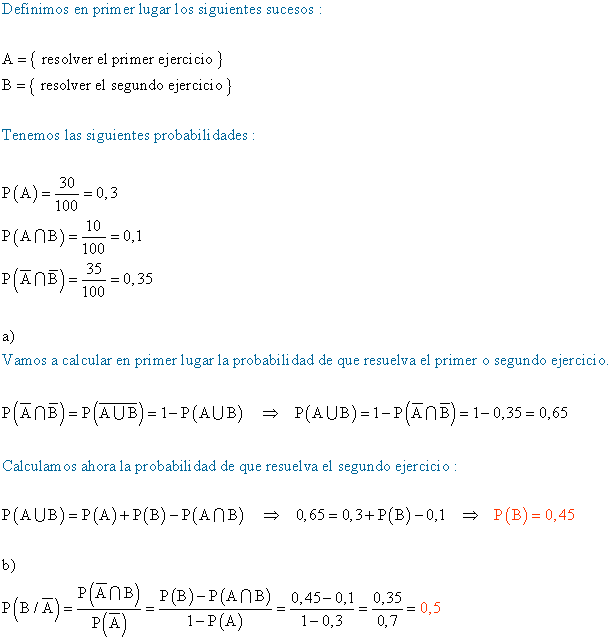
8) Una clase tiene 24 alumnos y todos ellos cursan inglés y matemáticas. La mitad aprueban inglés, 16 aprueban matemáticas, y 4 suspenden inglés y matemáticas.
a) Realiza una tabla de contingencia con los resultados de esta clase.
b) Calcula la probabilidad de que, al elegir un alumno de esta clase al azar, resulte que aprueba matemáticas y suspende inglés.
c) En esta clase, ¿son independientes los sucesos "aprobar inglés" y "aprobar matemáticas"?
a)
| Aprueba inglés | Suspende ingés | Total | |
|---|---|---|---|
| Aprueba matemáticas | 8 | 8 | 16 |
| Suspende matemáticas | 4 | 4 | 8 |
| Total | 12 | 12 | 24 |

9) Una fábrica produce tornillos niquelados y dorados, siendo el 75 % de los tornillos que produce niqelados. El porcentaje de tornillos defectuosos producidos es del 4 % para los tornillos niquelados y del 5 % para los dorados. Se elige al azar un tornillo y resulta no ser defectuoso. ¿Cuál es la probabilidad de que sea niquelado?

10) En un experimento aleatorio consistente en lanzar simultáneamente tres dados equilibrados de seis caras se pide calcular la probabilidad de obtener :
a) Tres unos.
b) Al menos un dos.
c) Tres números distintos.
d) Una suma de 4.

11) Una caja con una docena de huevos contiene dos de ellos rotos. Se extraen al azar y sin reemplazamiento cuatro huevos. Calcula la probabilidad de extraer :
a) Los cuatro huevos en un buen estado.
b) De entre los cuatro huevos, exactamente uno roto.

12) Se realiza una encuesta sobre la aceptación de dos productos A y B entre la población. El 45 % de la población consume el producto A, el 30 % consume el producto B y el 20 % consume ambos productos. Seleccionado un individuo de esa población al azar, se pide:
a) Si consume el producto A, calcular la probabilidad de que consuma el producto B.
b) Si consume el producto B, calcular la probabilidad de que no consuma el producto A.
c) Calcular la probabilidad de que no consuma ni A ni B.

13) De una baraja de cuarenta cartas se extraen sucesivamente tres cartas al azar. Determina la probabilidad de obtener :
a) Tres reyes.
b) Una figura en la primera carta, un cinco en la segunda y un seis en la tercera.
c) Un as, un tres y un seis en cualquier orden.

14) Un ordenador personal tiene cargados dos programas antivirus A1 y A2 que actúan simultánea e independientemente. Ante la presencia de un virus, el programa A1 lo detecta con una probabilidad de 0,9 y el programa A2 lo detecta con una probabilidad de 0,8. Calcular de forma razonada :
a) La probabilidad de que un virus cualquiera sea detectado.
b) La probabilidad de que un virus sea detectado por el programa A1 y no por A2.

15) Se extraen cuatro cartas de una baraja española. Halla la probabilidad de que las cuatro cartas sean del mismo palo en los siguientes casos :
a) Con devolución de la carta a la baraja.
b) Sin devolución.

a)
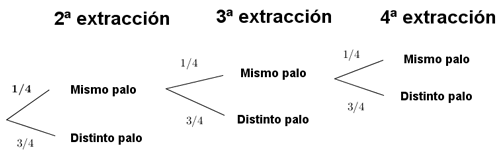
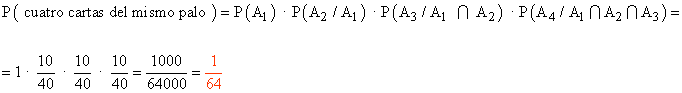
b)
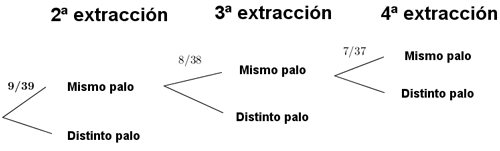
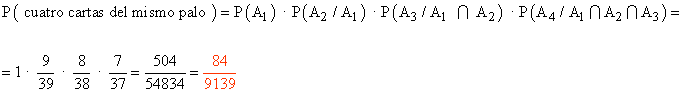
16) Tenemos una urna con 3 bolas rojas, 2 bolas verdes y 2 bolas azules.
Vamos a extraer 2 bolas al azar.
Definimos los sucesos R1 = { obtener una bola roja en la primera extracción }
y R2 = { obtener una bola roja en la segunda extracción}
Calcular las probabilidades de los sucesos si hay reemplazamiento de bola y si no hay reemplazamiento de bola.
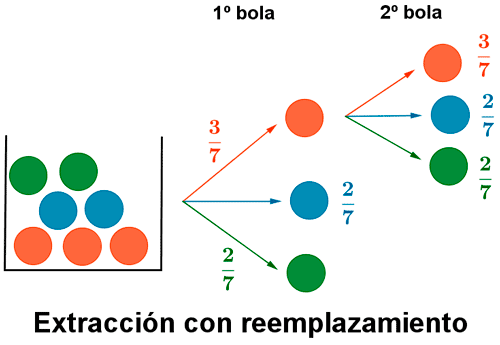
- Si la extracción es con reemplazamiento, los sucesos R1 y R2 son independientes.
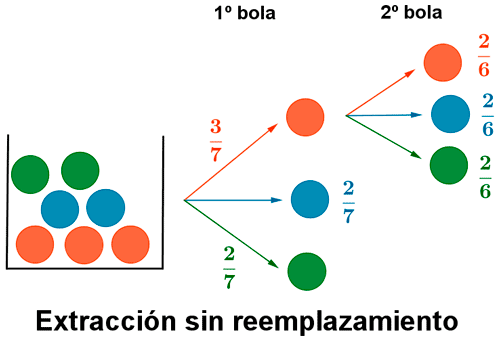
La probabilidad pedida es: - Si la extracción es sin reemplazamiento los sucesos R1 y R2 son dependientes.
La probabilidad pedida es:
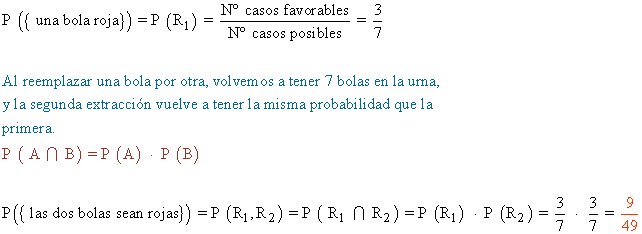

17) De una urna con 4 bolas azules y 3 bolas rojas, extraemos dos bolas. Calcular la probabilidad de que:
a) Ambas bolas sean azules.
b) La primera bola sea azul y la segunda bola sea roja.
c) Las dos bolas sean rojas.

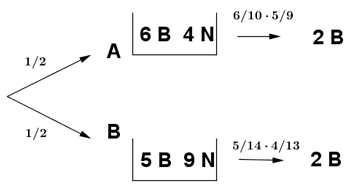
18) Una urna A contiene 6 bolas blancas y 4 negras. Otra urna B contiene 5 bolas blancas y 9 negras. Elegimos, a cara o cruz, una urna y extraemos dos bolas., que resultan ser blancas. Halla la probabilidad de que la urna elegida haya sido la A.

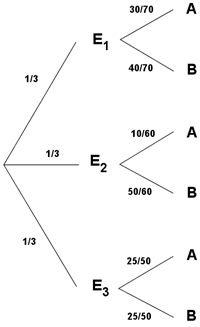
19) En un almacén hay tres tipos de estanterías en las que hay colocados dos tipos de productos: A y B. En la primera hay 30 de tipo A y 40 de tipo B; en la segunda, 10 de tipo A y 50 de tipo B, y en la tercera, 25 de tipo A y 25 de tipo B.
a) Si elegimos una estantería y un producto al azar, calcula la probabilidad de que este sea del tipo A.
b) Si elegimos un producto al azar de una de las estanterías y resulta que es del tipo B, halla la probabilidad de que proceda de la segunda estantería.
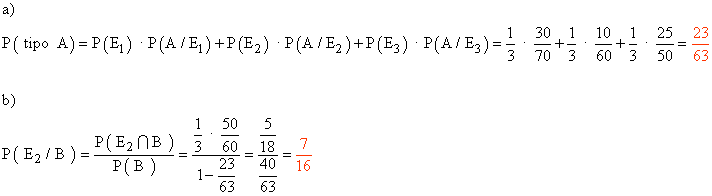
20) La probabilidad de que un chico sea elegido para formar parte de un coro es de 0,42 mientras que la probabilidad de que sea elegida una chica es de 0,55. Entre los aspirantes se elige al azar a un chico y una chica. Halla la probabilidad de que :
a) Los dos formen parte del coro.
b) Ninguno de los dos forme parte del coro.
c) Solo forme parte del coro la chica.
d) Al menos uno forme parte del coro.



 INICIO
INICIO