Distribución normal estándar o tipificada N(0, 1)

Una distribución normal estándar o tipificada es la que tiene μ = 0 y σ = 1 . La variable se representa con la letra z. Y la función de densidad correspondiente es:

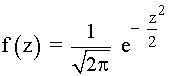
función de densidad normal estándar

La gráfica es simétrica con respecto al eje Y.
Los valores que nos dan las áreas correspondientes a las probabilidades del tipo P(Z ≤ z) se encuentran tabulados.
La función de distribución tiene por expresión:

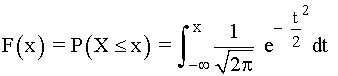
función de distribución normal estándar

Características de la función de densidad correspondiente a la normal estándar

Dominio o campo de existencia: toda la recta real : (- ∞ , + ∞)

Simetrías: la función es simétrica respecto al eje de ordenadas ya que la función es impar, es decir que f(x) = f(-x)

Corte con los ejes:
a) No tiene puntos de corte con el eje X.
b) Con el eje Y :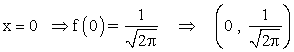

Asíntotas: 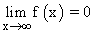por tanto el eje X es una asíntota

Crecimiento y decrecimiento: la función crece en el intervalo 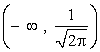y decrece en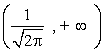

Máximos y mínimos : la función f(x) presenta un máximo en

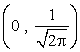
Puntos de inflexión: la función presenta dos puntos de inflexión I₁ e I₂ 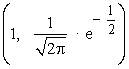en y en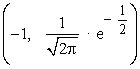

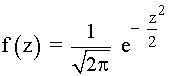
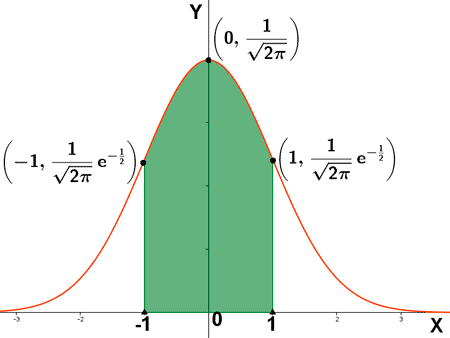
La representación gráfica se conoce como curva normal o campana de Gauss:

Como f(x) es una función de densidad, el área comprendida entre el eje X y la curva es 1.