Números combinatorios
Números combinatorios
Dado un número natural m, llamamos factorial de m, y lo denotamos por m! , al producto de m por todos los números naturales menores que él.
m! = m · (m - 1) · (m - 2) · ... · 3 · 2 · 1
0! = 1
1! = 1
Ejemplo 1:
Halla los factoriales de los 7 primeros números naturales:
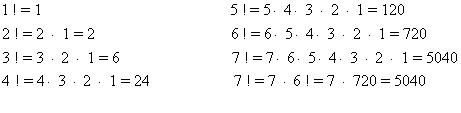
Dados dos números naturales m y n, tales que n ≤ m, definimos el número combinatorio "m sobre n" como:
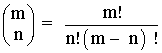
Ejemplo 2:
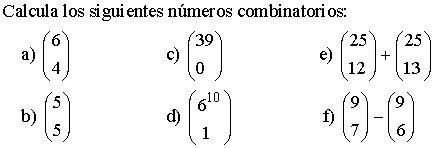
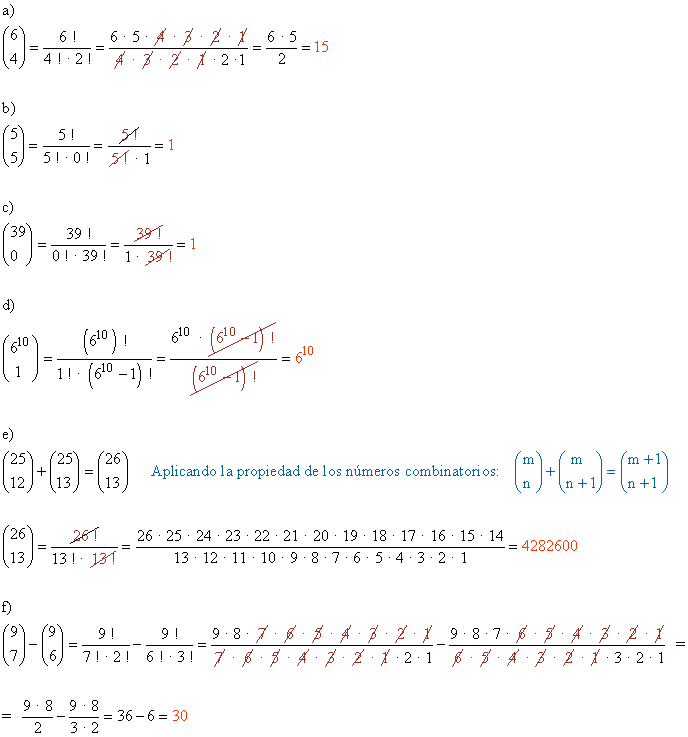
Propiedades de los números combinatorios
0! = 1
1! = 1
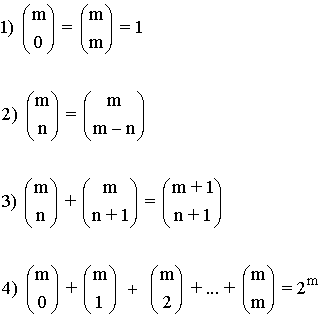
Ejemplo 3:
![]()

Ejemplo 4:
![]()

Triangulo de Tartaglia o triángulo de Pascal
Para hallar los coeficientes del binomio de Newton nos podemos ayudar del triángulo de Tartaglia o triángulo de Pascal:
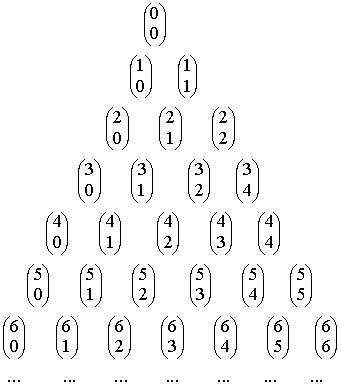
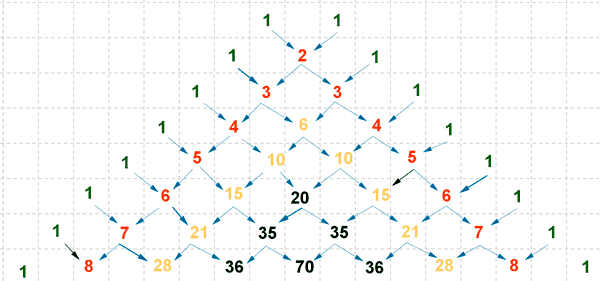
El triángulo de Tartaglia o de Pascal cumple todas las propiedades de los números combinatorios.
- Todas las filas empiezan y acaban en 1, que corresponden a los valores:
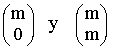
- El triángulo es simétrico ya que las filas son simétricas respecto de su punto medio.
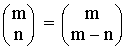
- Cualquier número intermedio es la suma de los dos números de la fila anterior entre los que está situado.
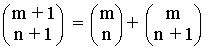
- La suma de todos los términos de una fila m cualquiera es 2m.
Ejemplo 5:
Halla los siguientes números combinatorios aplicando las propiedades:
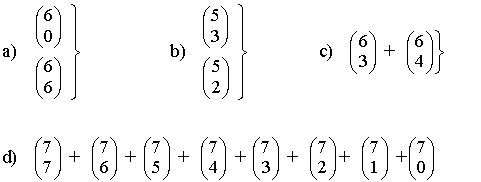



 INICIO
INICIO

