Problemas resueltos de variable aleatoria discreta
1) Considera el experimento " número obtenido " al lanzar un dado. Escribe la función de probabilidad y la función de distribución correspondiente a este experimento.
2) Sea el experimento "lanzar dos monedas al aire" y sea X la variable aleatoria discreta que asigna a cada elemento del espacio muestral el número de cruces. Escribir su función de probabilidad y su función de distribución.
3) Se lanzan dos dados cúbicos con las caras numeradas del 1 al 6. Se considera la variable X, que asigna a cada elemento del espacio muestral la suma de las caras obtenidas. Indica su función de distribución y su función de probabilidad.
a) Indica su función de distribución y su función de probabilidad.
b) Hallar la media y desviación típica.
4) En una bolsa hay bolas numeradas : nueve bolas con un 1, cinco bolas con un 2 y seis bolas con un 3. Se extrae una bola al azar. Representar las funciones de probabilidad y distribución.
5) La distribución de probabilidad de una variable aleatorio discreta viene dada por :
| xi | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| pi | 0,3 | 0,35 | k | 0,2 |
a) Halla k para que se trate de una función de probabilidad.
b) Representa gráficamente la función de probabilidad.
c) Halla P ( x ≤ 4 ) y P ( 2 ≤ x ≤ 4 ).
6) La función de probabilidad de una variable discreta es :
| xi | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| pi | 0,1 | a | b | c | 0,2 |
Sabiendo que P ( x ≤ 2 ) = 0,7 y que P ( x ≥ 2 ) = 0,75 hallar su esperanza matemática y su desviación típica.
7) Calcula la esperanza, la varianza y la desviación típica de la variable aleatoria X, cuya función de probabilidad viene dada por la tabla:
| x | -3 | -1 | 3 | 4 |
|---|---|---|---|---|
| f(x) | 0,2 | 0,4 | 0,3 | 0,1 |
8) Lanzamos 3 monedas al aire. Definimos la variable aleatoria 'número de cruces obtenidas' .
a) Encuentra el espacio muestral.
b) ¿Qué valores toma esta variable aleatoria?
c) Construye la distribución de probabilidad.
d) Calcula la esperanza matemática, la varianza y la desviación típica de esta variable aleatoria.
1) Considera el experimento " número obtenido " al lanzar un dado. Escribe la función de probabilidad y la función de distribución correspondiente a este experimento.
Reflejamos en una tabla el espacio muestral, así como los valores de X asociados a cada elemento del espacio muestral. Además, asociamos la función de probabilidad a cada uno de ellos.
| Espacio muestral | xi | f ( xi ) = pi |
|---|---|---|
| 1 | 1 | 1 / 6 |
| 2 | 1 | 1 / 6 |
| 3 | 1 | 1 / 6 |
| 4 | 1 | 1 / 6 |
| 5 | 1 | 1 / 6 |
| 6 | 1 | 1 / 6 |
A partir de la función de probabilidad obtenemos la función de distribución de nuestra variable. La función de distribución viene determinada por la expresión F ( x ) = P ( X ≤ x )
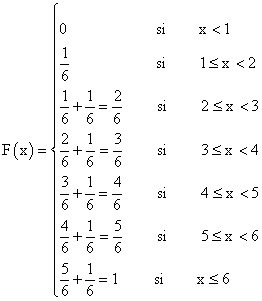
1) Sea el experimento "lanzar dos monedas al aire" y sea X la variable aleatoria discreta que asigna a cada elemento del espacio muestral el número de cruces. Escribir su función de probabilidad y su función de distribución.
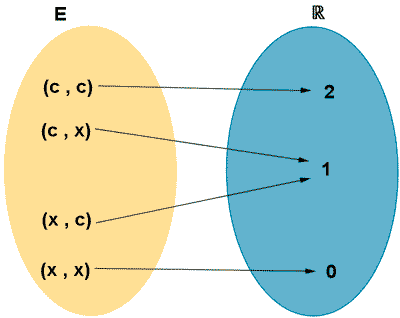
El espacio muestral del lanzamiento de dos monedas de un euro es:
E = { CC , CX , XC, XX}
Si se asocia a cada uno de los sucesos elementales del espacio muestral un número real, por ejemplo, el número de cruces, se obtiene una función del espacio muestral E en el conjunto de los número reales.
Esta función es una variable aleatoria tiene de recorrido el conjunto finito {0 , 1, 2}
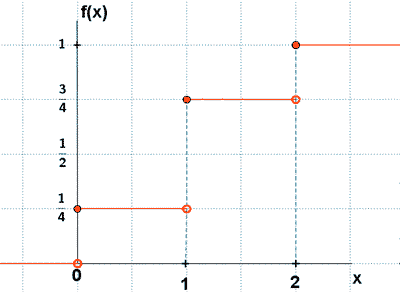
P (X = 0) = P( {(x, x)} ) = 1/4
P(X = 1) = P( {(c, x)}, {x, c} ) = 1/2
P(X = 2) = P( {(c, c)} ) = 1/4
| 0 | 1 | 2 | |
| 1/4 | 1/2 | 1/4 |
Esta correspondencia de probabilidades se llama distribución de probabilidad.
Obtenemos las funciones de probabilidad:
| 0 | 1 | 2 | |
| 1/4 | 1/2 | 1/4 |
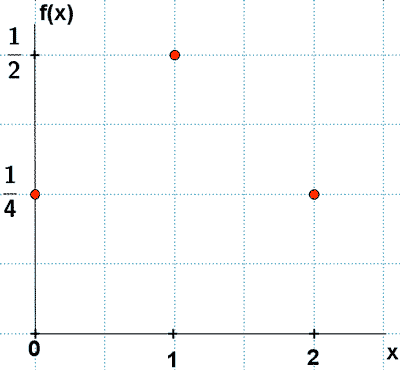
Nuestra función de distribución sería:
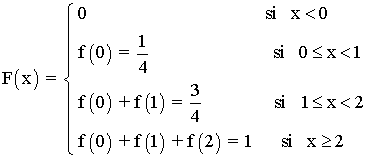
2) Se lanzan dos dados cúbicos con las caras numeradas del 1 al 6. Se considera la variable X, que asigna a cada elemento del espacio muestral la suma de las caras obtenidas.
a) Indica su función de distribución y su función de probabilidad.
b) Hallar la media y desviación típica.
a)
Recogemos en una tabla los posibles valores de la variable X junto con los elementos del espacio muestral asociados a dichos valores. Obtenemos así su función de probabilidad.
| Espacio muestral | xi | f ( xi ) = pi |
|---|---|---|
( 1, 1 ) |
2 | 1 / 36 |
( 1, 2 ) ( 2, 1 ) |
3 | 2 / 36 |
( 1, 3 ) ( 2, 2 ) ( 2, 1 ) |
4 | 3 / 36 |
( 1, 4 ) ( 2, 3 ) ( 3, 2 ) ( 4, 1 ) |
5 | 4 / 36 |
( 1, 5 ) ( 2, 4 ) ( 3, 3 ) ( 4, 2 ) ( 5, 1 ) |
6 | 5 / 36 |
( 1, 6 ) ( 2, 5 ) ( 3, 4 ) ( 4, 3 ) ( 5, 2 ) ( 6, 1 ) |
7 | 6 / 36 |
( 2, 6 ) ( 3, 5 ) ( 4, 4 ) ( 5, 3 ) ( 6, 2 ) |
8 | 5 / 36 |
( 3, 6 ) ( 4, 5 ) ( 5, 4 ) ( 6, 3 ) |
9 | 4 / 36 |
( 4, 6 ) ( 5, 5 ) ( 6, 4 ) |
10 | 3 / 36 |
( 5, 6 ) ( 6, 5 ) |
11 | 2 / 36 |
( 6, 6 ) |
12 | 1 / 36 |
A partir de la función de probabilidad obtenemos la función de distribución de nuestra variable. La función de distribución viene determinada por la expresión F ( x ) = P ( X ≤ x )
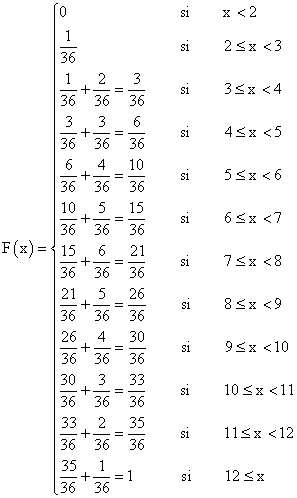
b)
| xi | pi | pi · xi | pi · xi2 |
|---|---|---|---|
| 2 | 1 / 36 | 2 / 36 | 4 / 36 |
| 3 | 2 / 36 | 6 / 36 | 18 / 36 |
| 4 | 3 / 36 | 12 / 36 | 48 / 36 |
| 5 | 4 / 36 | 20 / 36 | 100 / 36 |
| 6 | 5 / 36 | 30 / 36 | 180 / 36 |
| 7 | 6 / 36 | 42 / 36 | 294 / 36 |
| 8 | 5 / 36 | 40 / 36 | 320 / 36 |
| 9 | 4 / 36 | 36 / 36 | 324 / 36 |
| 10 | 3 / 36 | 30 / 36 | 300 / 36 |
| 11 | 2 / 36 | 22 / 36 | 242 / 36 |
| 12 | 1 / 36 | 12 / 36 | 144 / 36 |
| Sumatorios | 252 / 36 | 1974 / 36 | |
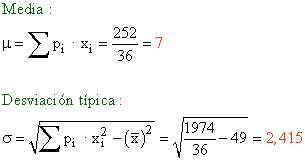
4) En una bolsa hay bolas numeradas : nueve bolas con un 1, cinco bolas con un 2 y seis bolas con un 3. Se extrae una bola al azar. Representar las funciones de probabilidad y distribución.
Función de probabilidad.
La recogemos en una tabla donde aparezcan los elementos del espacio muestral, asocidos cada uno a los casos favorables y la probabilidad asociada a cada uno de ellos.
| xi | F ( xi ) = pi |
|---|---|
| 1 | 9 / 20 |
| 2 | 5 / 20 |
| 3 | 6 / 20 |
Función de distribución.
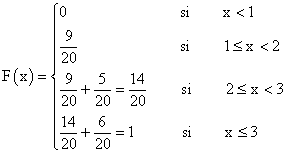
5) La distribución de probabilidad de una variable aleatorio discreta viene dada por :
| xi | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| pi | 0,3 | 0,35 | k | 0,2 |
a) Halla k para que se trate de una función de probabilidad.
b) Representa gráficamente la función de probabilidad.
c) Halla P ( x ≤ 4 ) y P ( 2 ≤ x ≤ 4 ).
a)
k = 1 - 0,3 - 0.35 - 0.2 = 0,15
b)
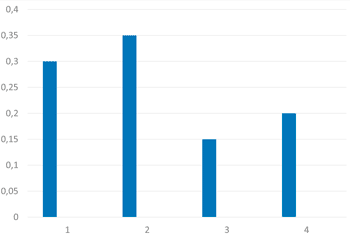
c)
P ( x ≤ 4 ) = 1
P ( 2 ≤ x ≤ 4 ) = 0,25 + 0,2 = 0,45
6) La función de probabilidad de una variable discreta es :
| xi | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| pi | 0,1 | a | b | c | 0,2 |
Sabiendo que P ( x ≤ 2 ) = 0,7 y que P ( x ≥ 2 ) = 0,75 hallar su esperanza matemática y su desviación típica.
Hallamos en primer lugar la función de distribución F ( x ) = P ( X ≤ x ) :
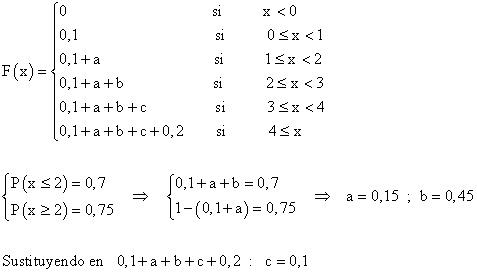
| xi | pi | xi · pi | xi2 | xi2 · pi |
|---|---|---|---|---|
| 0 | 0,1 | 0 | 0 | 0 |
| 1 | 0,15 | 0,15 | 1 | 0,15 |
| 2 | 0,45 | 0,9 | 4 | 1,8 |
| 3 | 0,1 | 0,3 | 9 | 0,9 |
| 4 | 0,2 | 0,8 | 16 | 3,2 |
| Sumatorios | 2,15 | 6,05 | ||
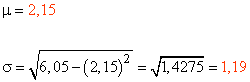
7) Calcula la esperanza, la varianza y la desviación típica de la variable aleatoria X, cuya función de probabilidad viene dada por la tabla:
| x | -3 | -1 | 3 | 4 |
|---|---|---|---|---|
| f(x) | 0,2 | 0,4 | 0,3 | 0,1 |
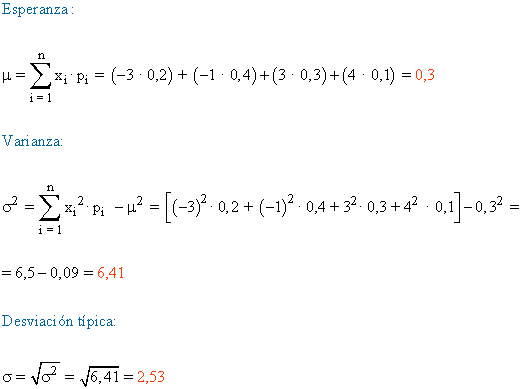
8) Lanzamos 3 monedas al aire. Definimos la variable aleatoria 'número de cruces obtenidas' .
a) Encuentra el espacio muestral.
b) ¿Qué valores toma esta variable aleatoria?
c) Construye la distribución de probabilidad.
d) Calcula la esperanza matemática, la varianza y la desviación típica de esta variable aleatoria.
a) El espacio muestral asociado a 'lanzar 3 monedas al aire' es:
E = {XXX, XXC, CXC, CXX, XCC, CXC, CCX, CCC}
b) La variable aleatoria X = nº de cruces obtenidas en cada lanzamiento, toma los valores 0, 1, 2 y 3. Por tanto podemos afirmar que se trata de una variable aleatoria discreta.
c) La distribución de la probabilidad es:
| X = nº de cruces en cada lanzamiento | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| Pi = P(X = xi) | 1/8 | 3/8 | 3/8 | 1/8 |
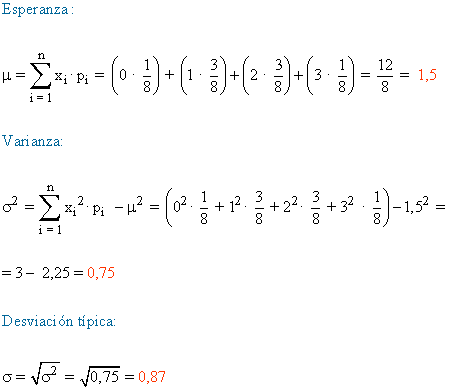


 INICIO
INICIO