Distribuciones de probabilidad de una variable continua
Función de densidad
a) f(x) ≥ 0 , para todo x de la variable.
b) El área comprendida entre el eje X y la función f(x) es 1.
Ejemplo 1:
Calcular k para que la función dada sea una función de densidad.
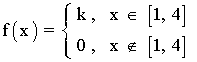
Hallar las probabilidades:
a) P(2 ≤ x < 3)
b) P(2 ≤ x < 4)
c) P(2 ≤ x < 9)

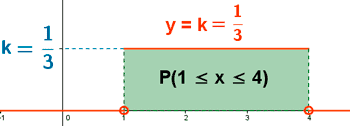
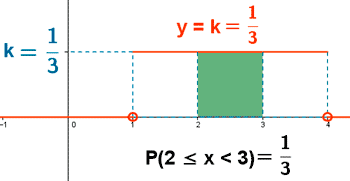
Ejemplo 2:
Calcular m para que la función dada sea una función de densidad.
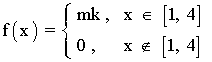
Hallar P(2 < x < 3)

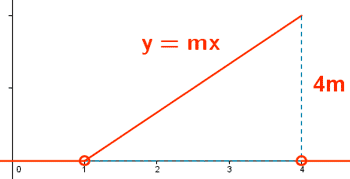
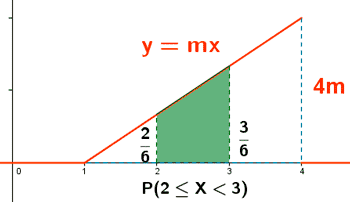
Función de distribución
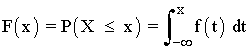
P(a ≤ X ≤ b) = área delimitada por f(x), el eje X y las rectas x = a y x = b.
Como consecuencia: P(a ≤ X ≤ b) = F(b) - F(a)
F'(x) = f(x)
Ejemplo 3:
Hallar la función de distribución de la variable aleatoria cuya función de densidad es:
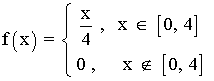

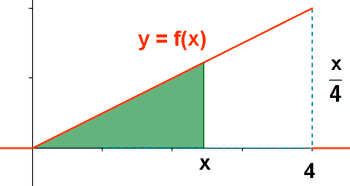
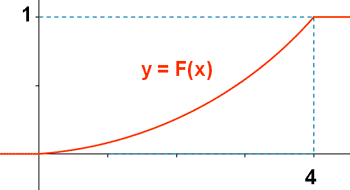
Ejemplo 4:
Considera la siguiente función :
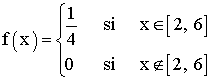
a) Comprueba que es una función de densidad.
b) Halla la función de distribución F de la variable aleatoria X cuya función de densidad es f y represéntala gráficamente.
c) Calcula P ( 3,6 ≤ X ≤ 5,2 )
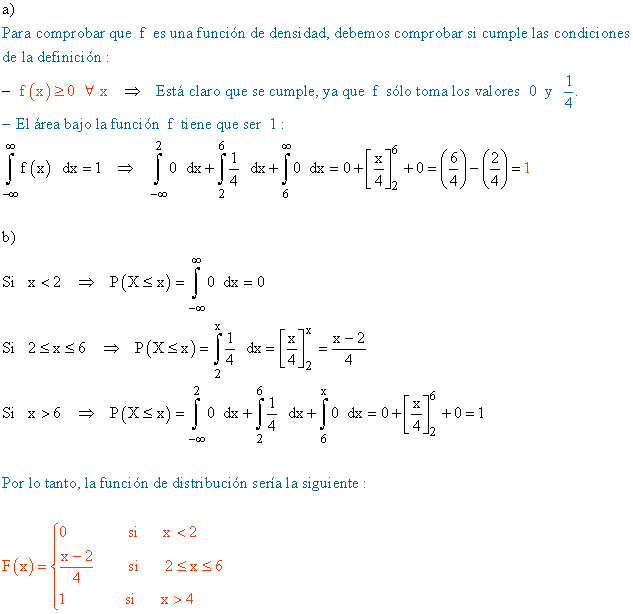
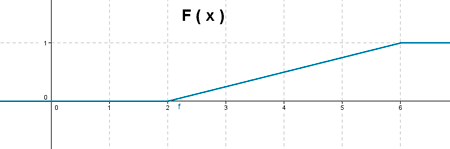
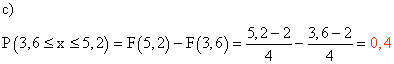


 INICIO
INICIO

