Parámetros de una variable aleatoria discreta
| Variable aleatoria X, que toma valores x1, ..., xi, ... , x n | Media aritmética o esperanza: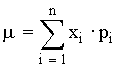 |
Varianza: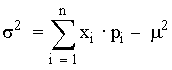 |
Desviación típica: |
|---|
Ejemplo 1:
Calcula la esperanza, la varianza y la desviación típica de la variable aleatoria X, cuya función de probabilidad viene dada por la tabla:
| x | -3 | -1 | 3 | 4 |
|---|---|---|---|---|
| f(x) | 0,2 | 0,4 | 0,3 | 0,1 |
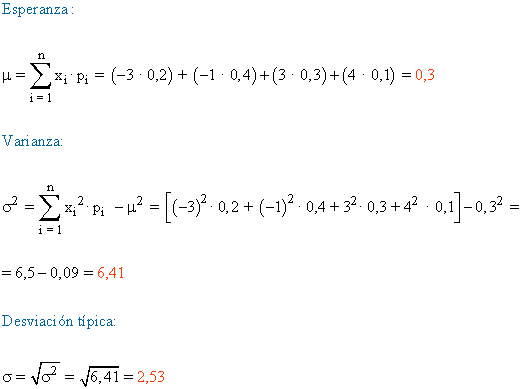
Ejemplo 2:
Lanzamos 3 monedas al aire. Definimos la variable aleatoria 'número de cruces obtenidas' .
a) Encuentra el espacio muestral.
b) ¿Qué valores toma esta variable aleatoria?
c) Construye la distribución de probabilidad.
d) Calcula la esperanza matemática, la varianza y la desviación típica de esta variable aleatoria.a) El espacio muestral asociado a 'lanzar 3 monedas al aire' es:
E = {XXX, XXC, CXC, CXX, XCC, CXC, CCX, CCC}
b) La variable aleatoria X = nº de cruces obtenidas en cada lanzamiento, toma los valores 0, 1, 2 y 3. Por tanto podemos afirmar que se trata de una variable aleatoria discreta.
c) La distribución de la probabilidad es:
| X = nº de cruces en cada lanzamiento | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| Pi = P(X = xi) | 1/8 | 3/8 | 3/8 | 1/8 |
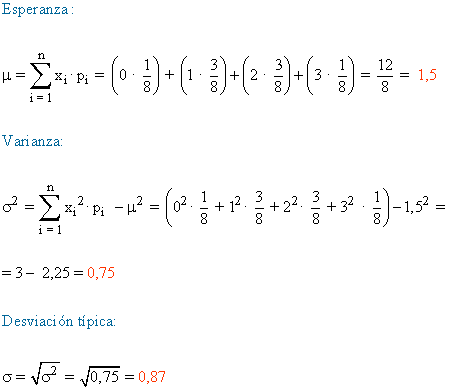


 INICIO
INICIO

