Ejercicios de factorización y simplificación de números complejos
1 ) Factorizar los siguientes polinomios.
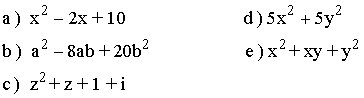
2 ) Simplificar las siguientes expresiones.
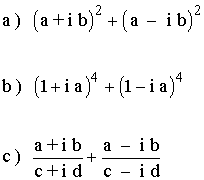
3 ) Expresar en forma binómica la siguiente ecuación de números complejos.
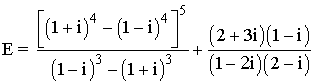
4 ) Representar en forma trigonométrica el número complejo.
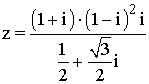
5 ) Dados los números complejos z1= 2 - i y z2= 3 + 6 i determinar el número x que verifica cada una de las siguientes igualdades.
![]()
6 ) Hallar las soluciones de las siguientes ecuaciones:

1 ) Factorizar los siguientes polinomios.
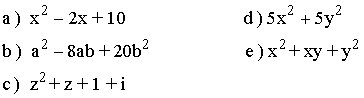

2 ) Simplificar las siguientes expresiones.
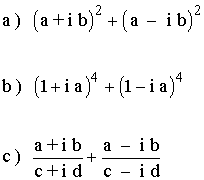
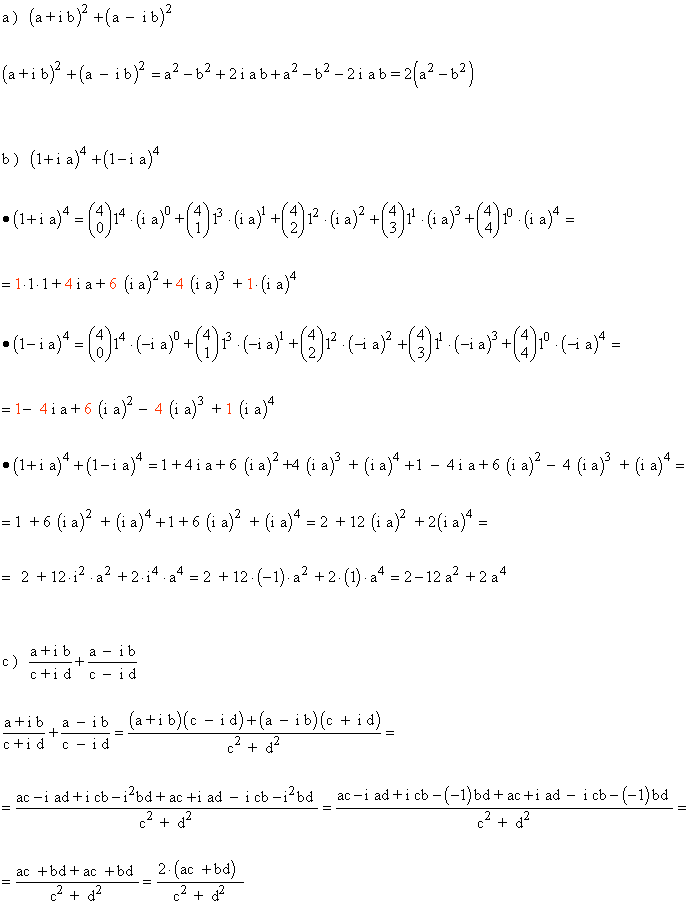
3 ) Expresar en forma binómica la siguiente ecuación de números complejos.
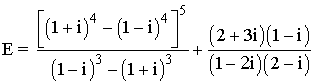
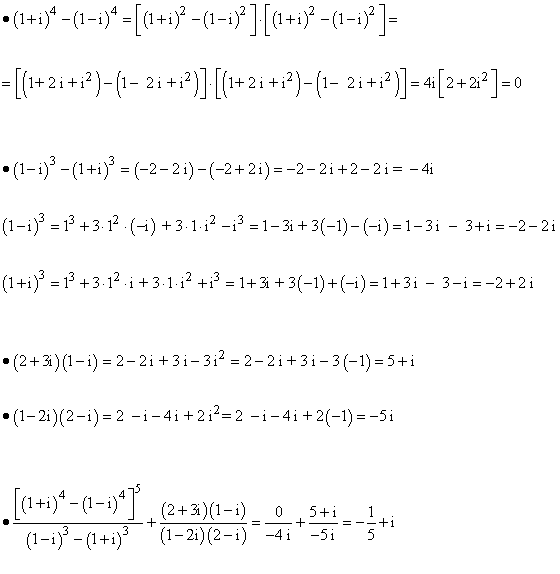
4 ) Representar en forma trigonométrica el número complejo.
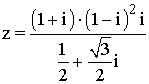
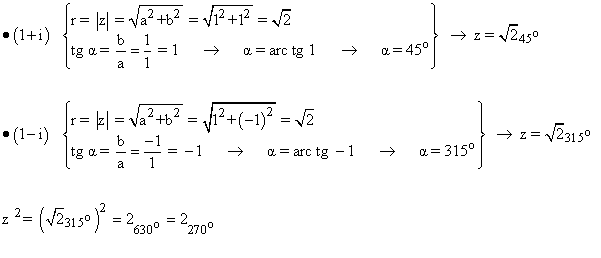
Sabemos que el ángulo que corresponden a la tangente de -1 es 135º y 315º. Como el afijo de z está en el cuarto cuadrante, el ángulo del número complejo es 315o
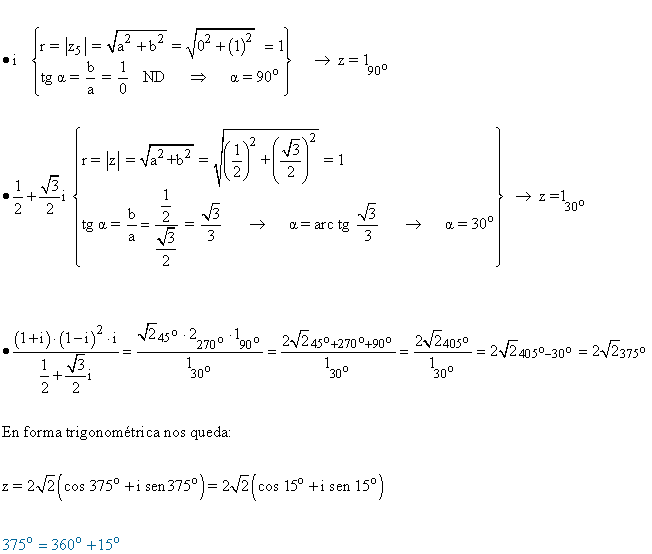
5 ) Dados los números complejos z1= 2 - i y z2= 3 + 6 i determinar el número x que verifica cada una de las siguientes igualdades.
![]()
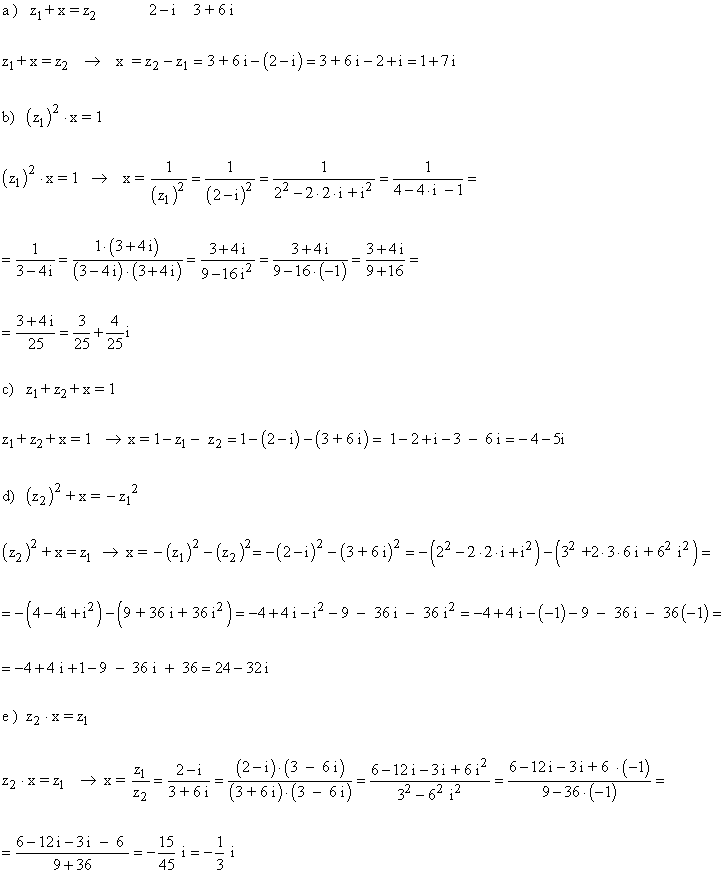
6 ) Hallar las soluciones de las siguientes ecuaciones:

![]()
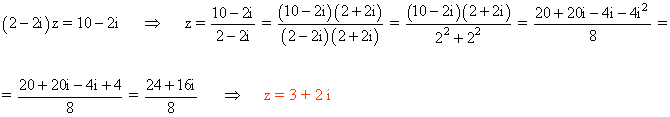
![]()
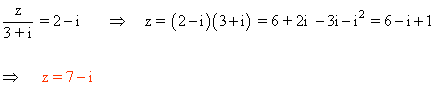
![]()

![]()
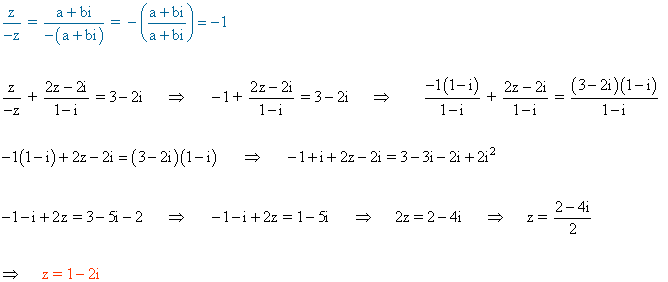


 INICIO
INICIO