Ley de Laplace

Un experimento es regular cuando todos sus sucesos elementales tienen la misma probabilidad,
es decir, son sucesos equiprobables.
Por ejemplo cuando se utiliza un dado correcto (que no esté trucado), una baraja de cartas
completa, etc.

Para aplicar esta regla se han de cumplir las siguientes condiciones:

• Los sucesos elementales tienen que ser equiprobables.
• Los resultados del experimento han de ser sucesos elementales.
• El número de posibles resultados debe ser finito.

Si aplicamos la regla de Laplace pueden ocurrir los siguientes casos:

• Si el espacio muestral de un experimento aleatorio está formado por n sucesos elementales,
  entonces la probabilidad de cada uno de ellos es:   1/n
• Si un suceso tiene k casos posibles, entonces su probabilidad es :    k/n

Ejemplo 1 :

Al girar una ruleta como la de la figura, ¿cuál es la probabilidad de cada color?

   

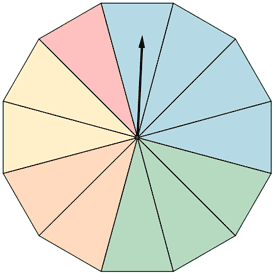
Al encontrarnos en una situación de equiprobabilidad, aplicamos la Regla de Laplace para poder calcular la probabilidad de cada color, teniendo en cuenta que la ruleta se encuentra dividida en 12 partes. Los sucesos elementales presentan la misma probabilidad.

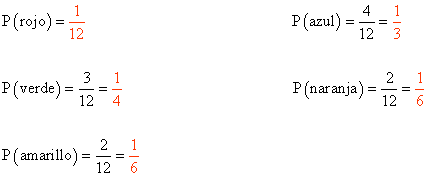
Ejemplo 2:

Si extraemos una bola al azar de una urna que contiene 3 bolas verdes, 5 bolas blancas
y 2 bolas azules, calcula la probabilidad de los sucesos A={obtener una bola verde} ,
B={obtener una bola blanca} y C={obtener una bola azul}.

Ejemplo 3 :

Si lanzamos un dado al aire, calcula la probabilidad de que ocurran los siguientes sucesos:
a) Sacar un 3.
b) Sacar un número par.
c) Sacar un número primo.
d) Sacar un número menos que 5.

Definimos en primer lugar el espacio muestral de mi experimento.

E = { 1, 2, 3, 4, 5, 6 }

Aplicando la regla de Laplace, calculamos ahora las probabilidades de cada uno de los sucesos.

Ejemplo 4 :

De la baraja de cartas española de 40 cartas se extrae una carta al azar. Calcula las probabilidades de los siguientes sucesos:
a) Sacar un múltiplo de 2.
b) Sacar un rey.
c) Sacar un oro.
d) Sacar una figura
e) Sacar una carta que no sea figura.
f) Sacar el as de espadas.
g) Sacar dos figuras iguales del mismo palo.

Aplicando la regla de Laplace, calculamos ahora las probabilidades de cada uno de los sucesos.

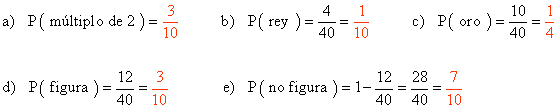
Ejemplo 5 :

Lanzamos dos veces un dado cúbico de seis caras y sumamos las puntuaciones obtenidas. Calcula la probabilidad de los sucesos elementales.

El espacio muestral de nuestro experimento es el siguiente:

E = { 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 }.

Sin embargo, los sucesos no son equiprobables, así que consideramos el experimento "lanzar un dado dos veces" y definimos su espacio muestral, cuyos sucesos sí son equiprobables.

E = { ( 1, 1 ), ( 1, 2 ), ( 1, 3 ), ( 1, 4 ), ( 1, 5 ), ( 1, 6 ), ( 2, 1 ), ( 2, 2 ), ( 2, 3 ), ( 2, 4 ), ( 2, 5 ), ( 2, 6 ), ( 3, 1 ), ( 3, 2 ), ( 3, 3 ), ( 3, 4 ), ( 3, 5 ), ( 3, 6 ), ( 4, 1 ), ( 4, 2 ), ( 4, 3 ), ( 4, 4 ), ( 4, 5 ), ( 4, 6 ), ( 5, 1 ), ( 5, 2 ), ( 5, 3 ), ( 5, 4 ), ( 5, 5 ), ( 5, 6 ), ( 6, 1 ), ( 6, 2 ), ( 6, 3 ), ( 6, 4 ), ( 6, 5 ), ( 6, 6 ) }

Por último, basta con ver qué sucesos de mi espacio muestral del experimento "lanzar un dado dos veces" favorece el espacio muestral del experimento "lanzar un dado dos veces y sumar sus puntuaciones".
El número de sucesos coincide con el número de variaciones con repetición de seis elementos tomados de dos en dos :

             VR_{6, 2} = 6² = 36

Aplicando la regla de Laplace, calculamos ahora las probabilidades de cada uno de los sucesos.

Suceso	Casos favorables	Nº de casos favorables	Probabilidad
{ 2 }	( 1, 1)	1	1 / 36
{ 3 }	( 1, 2 ), ( 2, 1 )	2	2 / 36
{ 4 }	( 1, 3 ), ( 3, 1 ), ( 2, 2 )	3	3 / 36
{ 5 }	( 1, 4 ), ( 2, 3 ), ( 3, 2 ), ( 4, 1 )	4	4 / 36
{ 6 }	( 1, 5 ), ( 2, 4 ), ( 3, 3 ), ( 4, 2 ), ( 5, 1 )	5	5 / 36
{ 7 }	( 1, 6 ), ( 2, 5 ), ( 3, 4 ), ( 4, 3 ), ( 5, 2 ), ( 6, 1)	6	6 / 36
{ 8 }	( 2, 6 ), ( 3, 5 ), ( 4, 4 ), ( 5, 3 ), ( 6, 2 )	5	5 / 36
{ 9 }	( 3, 6 ), ( 4, 5 ), ( 5, 4 ), ( 6, 3 )	4	4 / 36
{ 10 }	( 4, 6 ), ( 5, 5 ), ( 6, 4 )	3	3 / 36
{ 11 }	( 5, 6 ), ( 6, 5 )	2	2 / 36
{ 12 }	( 6, 6 )	1	1 / 36