Ejercicios resueltos de área y elementos notables de un triángulo
1 ) Decir que clase de triángulo es cada uno de los siguientes grupos de coordenadas:
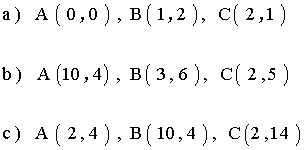
2 ) Hallar las coordenadas de los tres vértices del triángulo ABC, sabiendo que las coordenadas de los puntos medios de sus lados son:
![]()
3 ) Halla los vértices del triángulo cuyos lados están sobre las rectas r , s y t de ecuaciones:
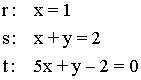
4 ) Sea el triángulo con los siguientes vértices:
![]()
5 ) Sea el triángulo con los siguientes vértices:
![]()
6 ) Dado el triángulo que tiene los siguientes vértices:
![]()
7 ) Dado el triángulo que tiene los siguientes vértices:
![]()
8 ) Dado el triángulo que tiene los siguientes vértices:
![]()
a ) El baricentro.
b ) El circuncentro.
c ) El ortocentro.
9 ) Dado el triángulo de vértices:
![]()
Calcular:
a ) El baricentro.
b ) Las ecuaciones de las tres alturas.
c ) El ortocentro.
d ) La recta de Euler.
10 ) Calcula el área limitada por la recta (x/3) + (y/6) = 1 el eje de abcisas y el eje de ordenadas.
11 ) Calcula el área del triángulo definido por las siguientes ecuaciones:
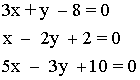
12 ) Calcula el área del triángulo de vértices:
![]()
13 ) Calcular la distancia del baricentro del triángulo a cada uno de sus lados, sabiendo que sus vértices son A (5 , 1) , B (1 , 7) y C (-1 , -3):
14 ) Dos de los vertices del triángulo ABC son A ( 1 , 5 ) y B ( 7 , 1 ).
a ) Calcular las coordenadas de C sabiendo que la recta x - 4 = 0 es la mediatriz del segmento BC.
b ) Calcula la ecuación de la altura h que parte de C.
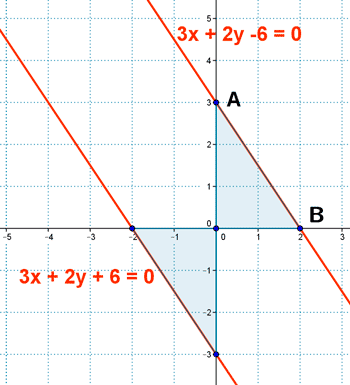
15 ) Determina la ecuación de una recta de pendiente -3/2 que forma con los ejes un triángulo de área igual a 3. ¿ Cúantas soluciones hay ?
16 ) En un triángulo cuyos vértices son los puntos A(2, 5), B(8, 3) y C(1, -2), calcula:
a) Baricentro
b) Circuncentro
c) Ortocentro
d) La recta de Euler
17 ) Calcula el incentro del triángulo cuyos vértices son los puntos A(2, 5) , B(8, 3) y C(1, -2).
1 ) Decir que clase de triángulo es cada uno de los siguientes grupos de coordenadas:
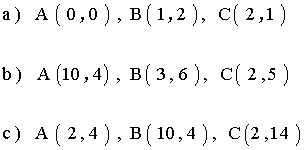

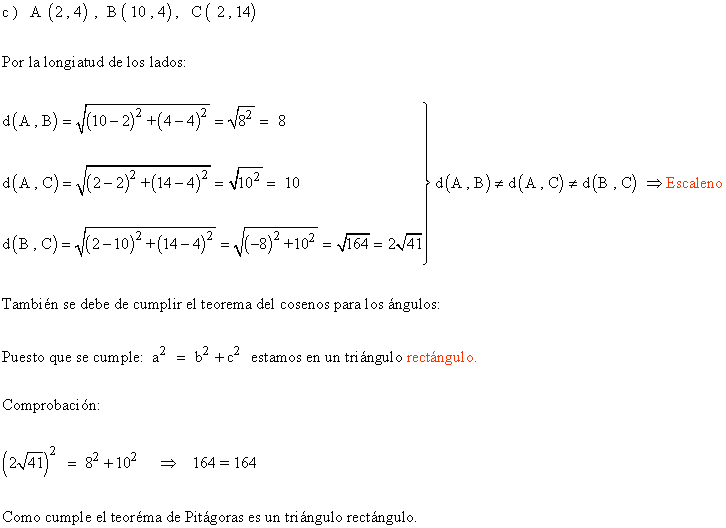
2 ) Hallar las coordenadas de los tres vértices del triángulo ABC, sabiendo que las coordenadas de los puntos medios de sus lados son:
![]()
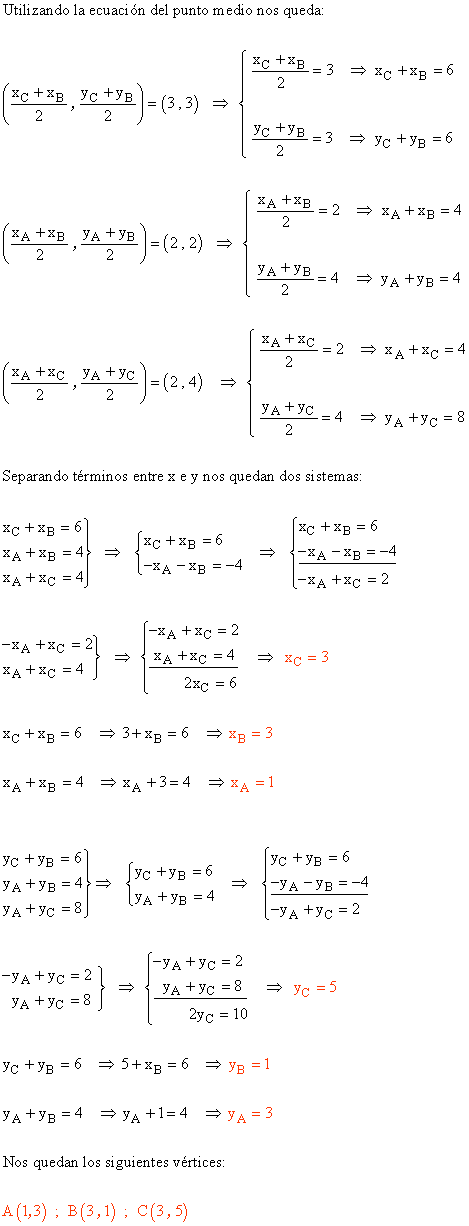
3 ) Halla los vértices del triángulo cuyos lados están sobre las rectas r , s y t de ecuaciones:
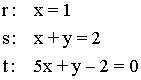

4 ) Sea el triángulo con los siguientes vértices:
![]()
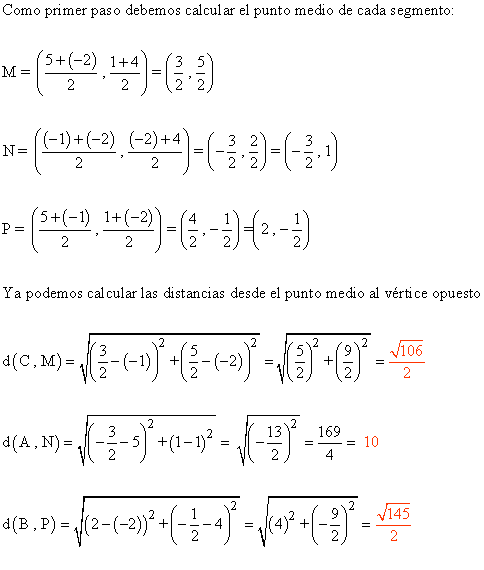
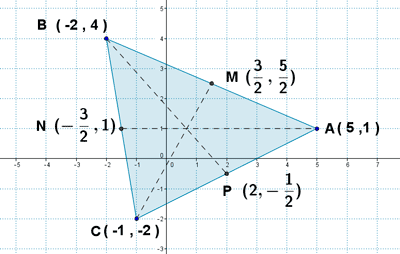
5 ) Sea el triángulo con los siguientes vértices:
![]()
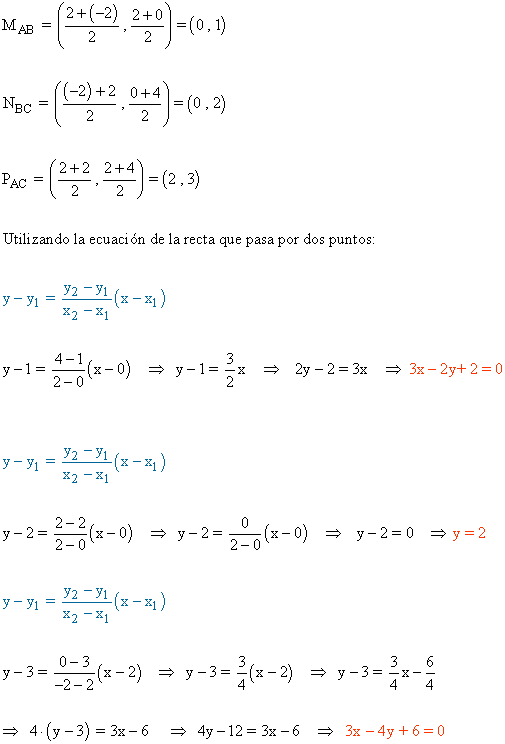
6 ) Dado el triángulo que tiene los siguientes vértices:
![]()
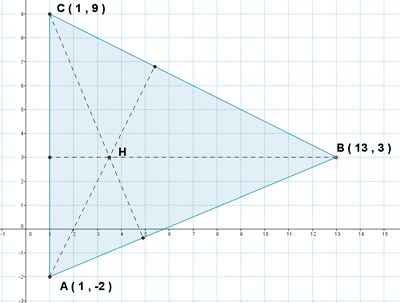

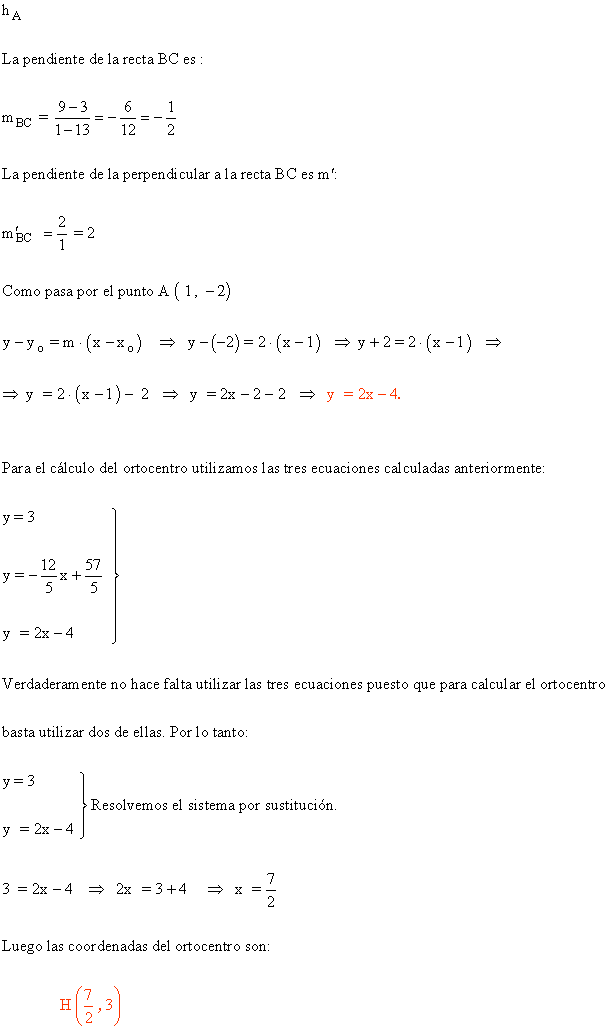
7 ) Dado el triángulo que tiene los siguientes vértices:
![]()
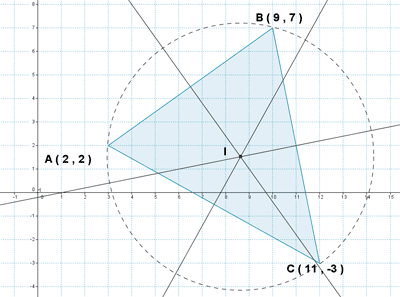

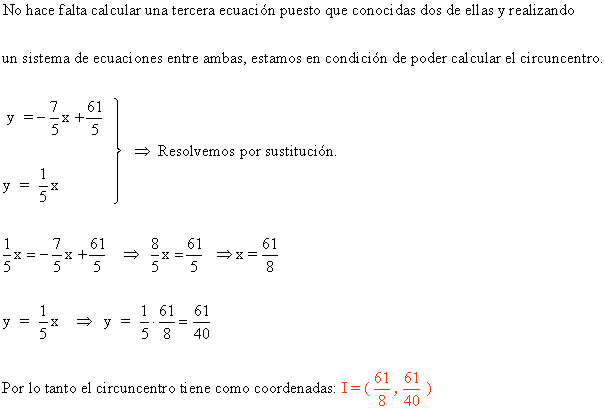
8 ) Dado el triángulo que tiene los siguientes vértices:
![]()
a ) El baricentro.
b ) El circuncentro.
c ) El ortocentro.
a ) Baricentro.
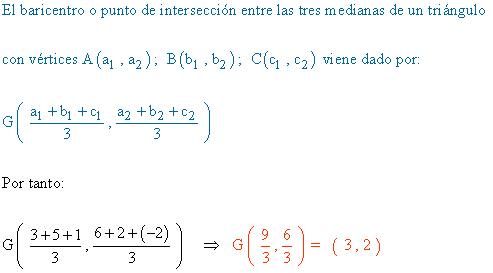
b ) Circuncentro.

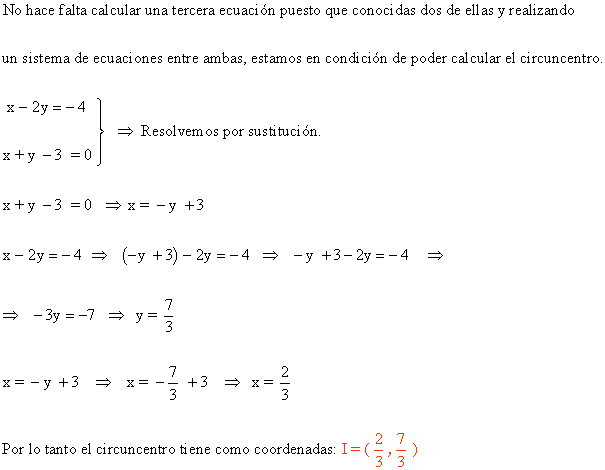
c ) Ortocentro.

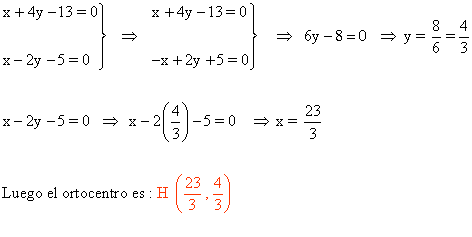
9 ) Dado el triángulo de vértices:
![]()
Calcular:
a ) El baricentro.
b ) Las ecuaciones de las tres alturas.
c ) El ortocentro.
d ) La recta de Euler.

b ) Ecuaciones de las tres alturas.
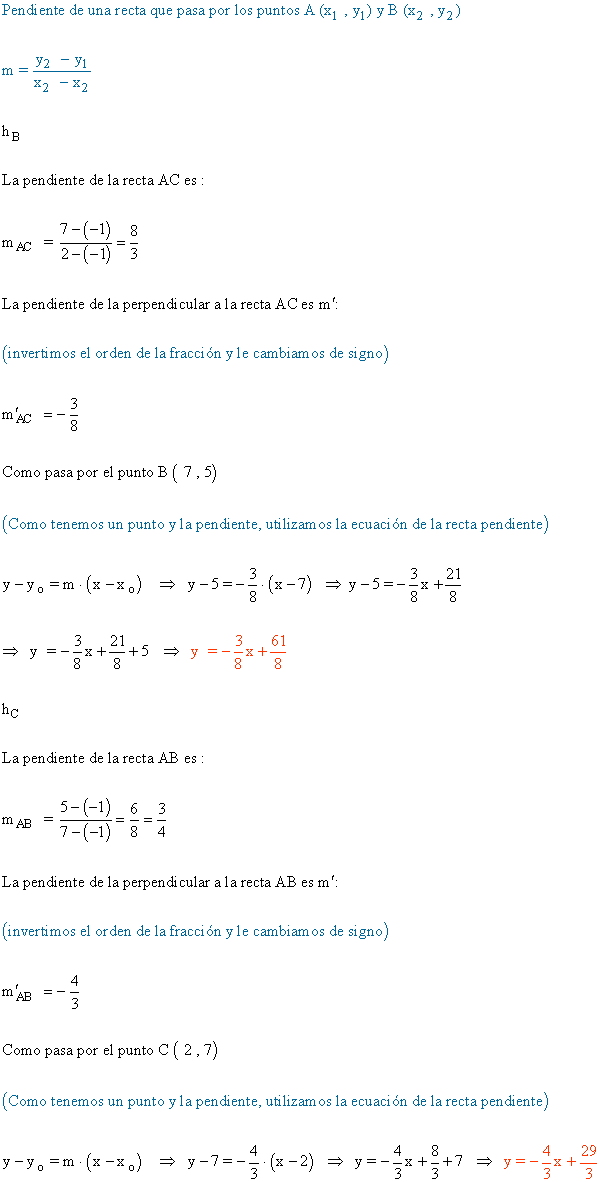

c ) El ortocentro.
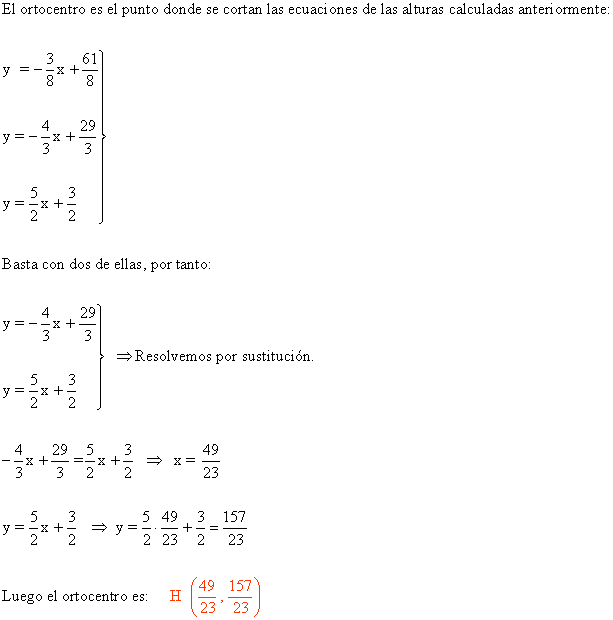
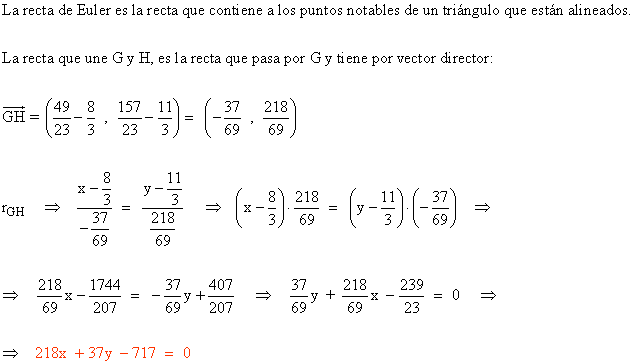
10 ) Calcula el área limitada por la recta (x/3) + (y/6) = 1 el eje de abcisas y el eje de ordenadas.

11 ) Calcula el área del triángulo definido por las siguientes ecuaciones:


12 ) Calcula el área del triángulo de vértices:
![]()

También podemos considerar otra altura y por la tanto su base perpendicualar a dicha altura.


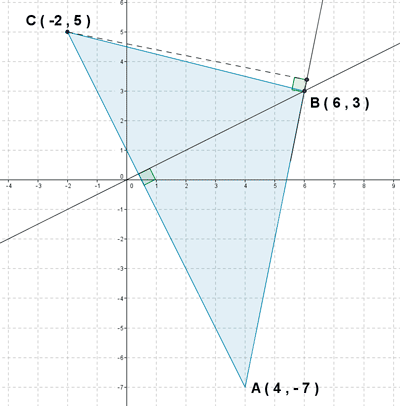
13 ) Calcular la distancia del baricentro del triángulo a cada uno de sus lados, sabiendo que sus vértices son A (5 , 1) , B (1 , 7) y C (-1 , -3):
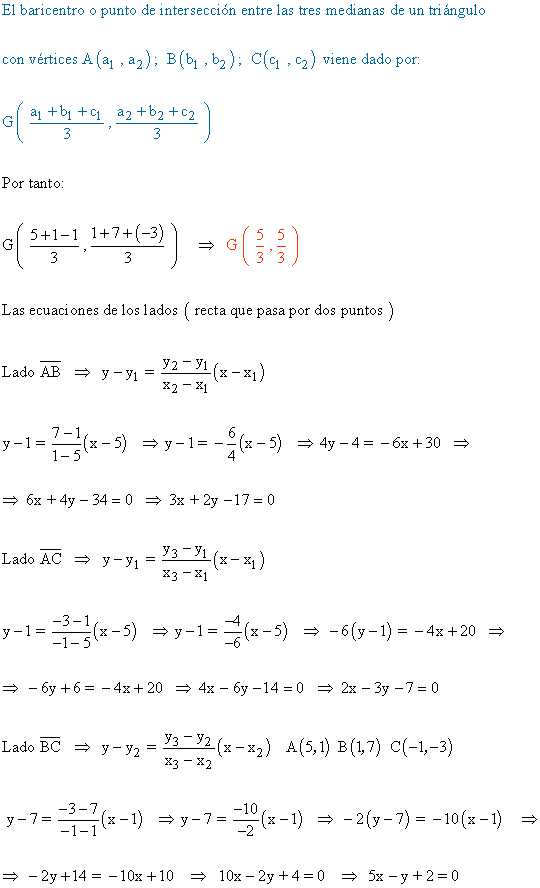
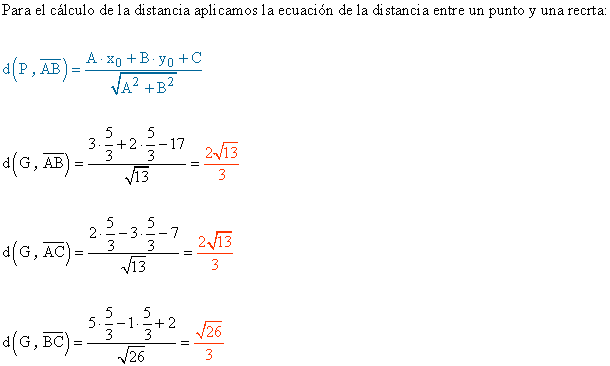
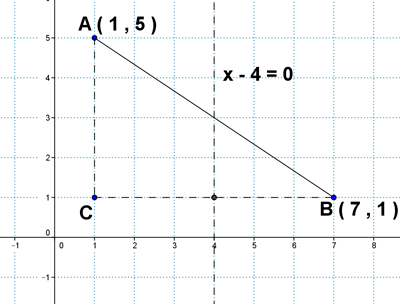
14 ) Dos de los vertices del triángulo ABC son A ( 1 , 5 ) y B ( 7 , 1 ).
a ) Calcular las coordenadas de C sabiendo que la recta x - 4 = 0 es la mediatriz del segmento BC.
b ) Calcula la ecuación de la altura h que parte de C.

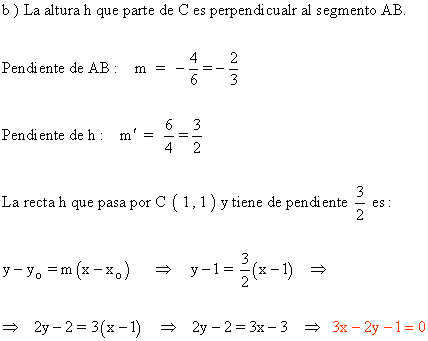
15 ) Determina la ecuación de una recta de pendiente -3/2 que forma con los ejes un triángulo de área igual a 3. ¿ Cúantas soluciones hay ?

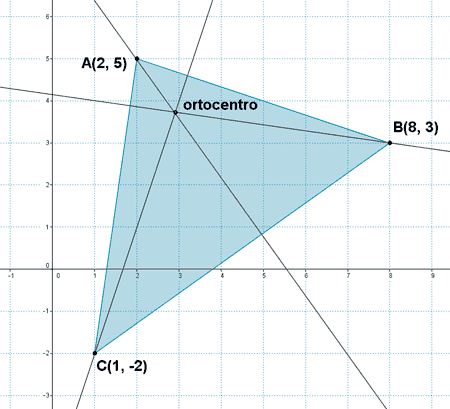
16 ) En un triángulo cuyos vértices son los puntos A(2, 5), B(8, 3) y C(1, -2), calcula:
a) Baricentro
b) Circuncentro
c) Ortocentro
d) La recta de Euler
(a) Baricentro
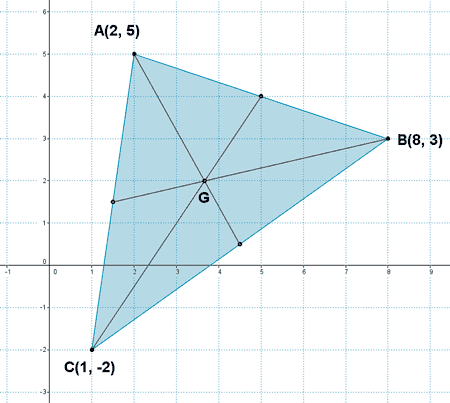
Utilizamos la fórmula anterior para calcular el baricentro:
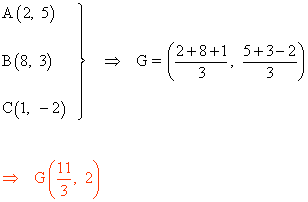
(b) Circuncentro
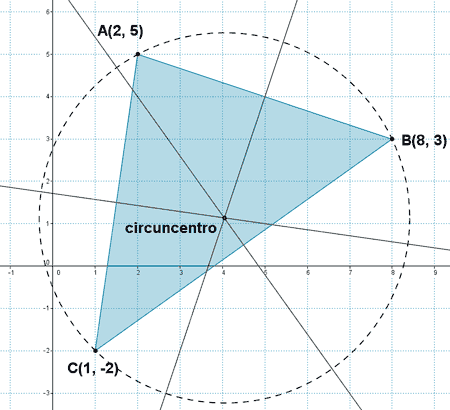
Calculamos el punto medio del segmento AB:
![]()
A continuación la pendiente de la mediatriz del segmento AB:
![]()
Aplicamos la ecuación punto pendiente con los datos anteriores:
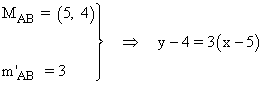
Por lo tanto, la mediatriz del segmento AB es:
![]()
Repetimos el proceso anterior para calcular la mediatriz del segmento AC:
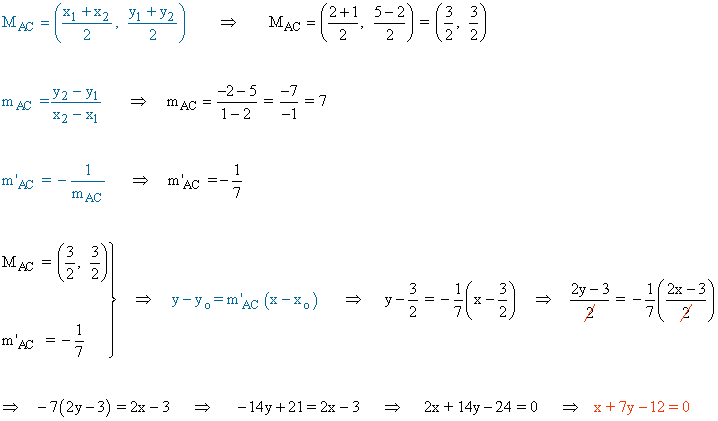
Repetimos el proceso anterior para calcular la mediatriz del segmento CB:
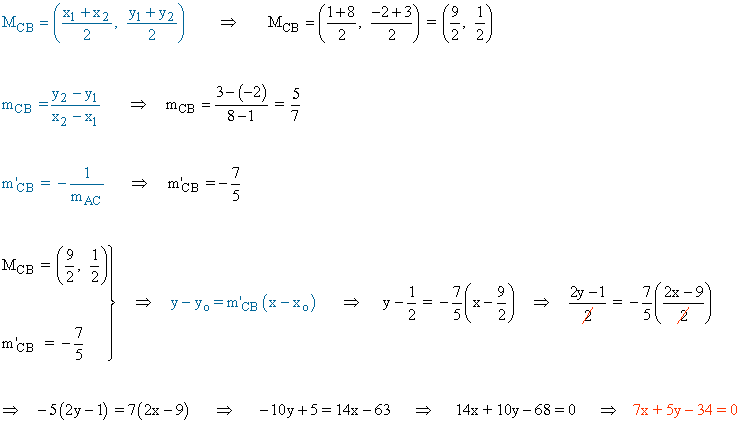
Por lo tanto, el punto de intersección de las tres mediatrices es el circuncentro. Aunque hemos calculado las tres mediatrices, para hallar el circuncentro basta con calcular el punto de intersección de dos de ellas::
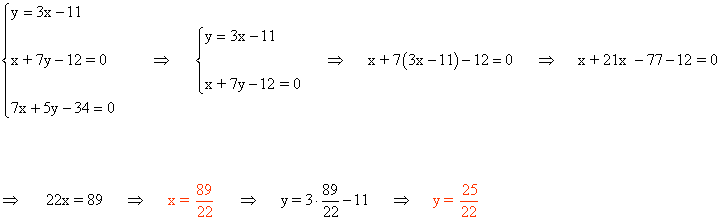
Es decir, el circuncentro del triángulo ABC es:
![]()
(c) Ortocentro
Calculamos en primer lugar la pendiente de la recta que pasa por los puntos A y B y la pendiente de su recta perpendicular::
![]()
Aplicamos la ecuación punto pendiente que pasa por el punto C y es perpendicular a la recta que pasa por A y B:
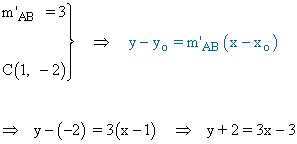
Por lo tanto, la altura del segmento AB viene dado por la recta:
![]()
Repetimos el proceso anterior para calcular la mediatriz del segmento AC:
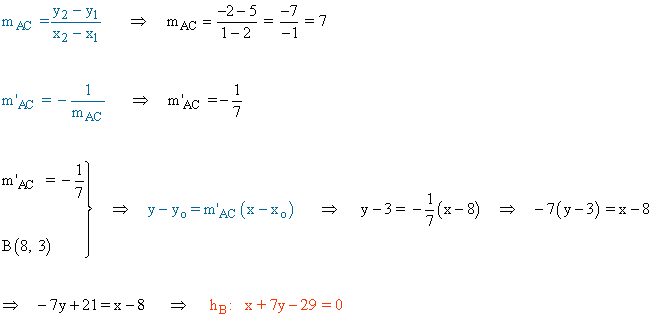
Repetimos el proceso anterior para calcular la mediatriz del segmento CB:
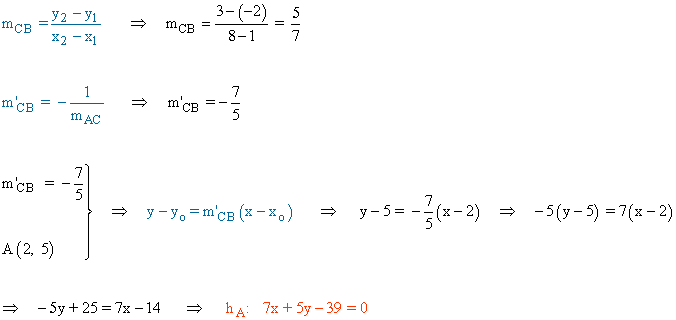
Calculamos la intersección de las tres rectas utilizando el método de reducción:
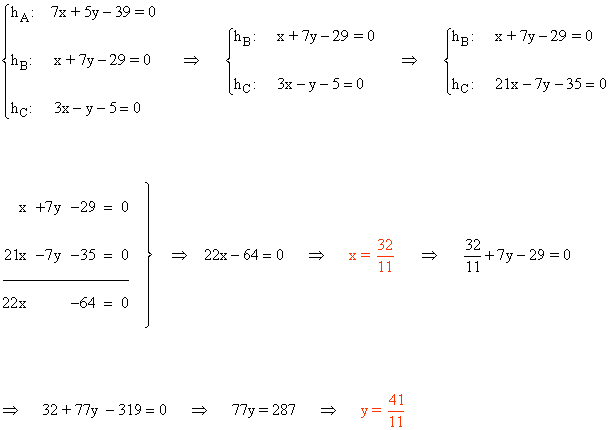
Por lo tanto, el ortocentro del triángulo ABC es:
![]()
(d) Recta de Euler
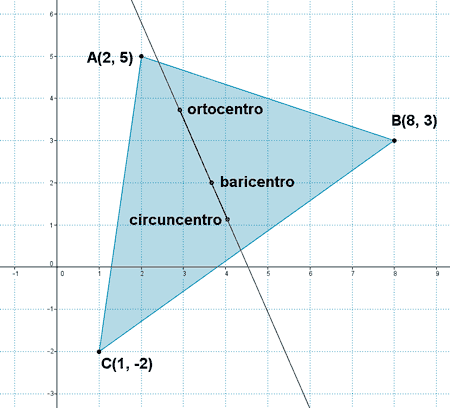
Los tres pontos notables son:

Calculamos la recta que pasa por G y H y verificamos que el punto C está contenido en dicha recta:
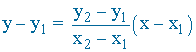
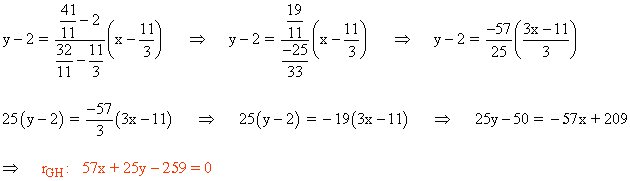
Por último, verificamos que el punto C está contenido en dicha recta:
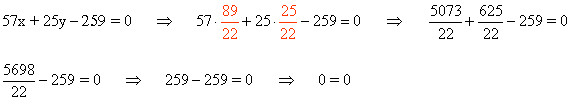
Por lo tanto, los tres puntos están alineados, es decir, pertenecen a la misma recta, denominada recta de Euler..
17 ) Calcula el incentro del triángulo cuyos vértices son los puntos A(2, 5) , B(8, 3) y C(1, -2).
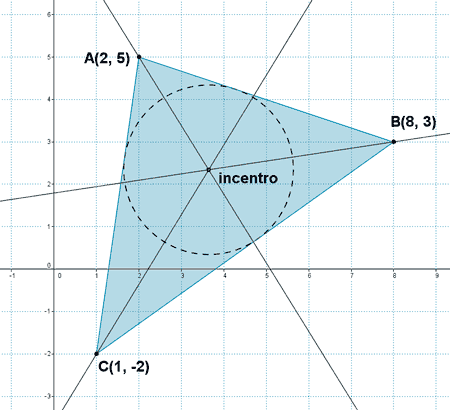
Para hallar las bisectrices necesitamos conocer las rectas que pasan por los vértices del triángulo, utilizando la ecuación que pasa por dos puntos:
![]()
Calculamos en primer lugar la recta que pasa por los puntos A y B:
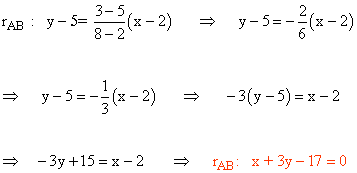
Calculamos de la misma manera las rectas que pasan por los puntos A y C y por los puntos B y C:
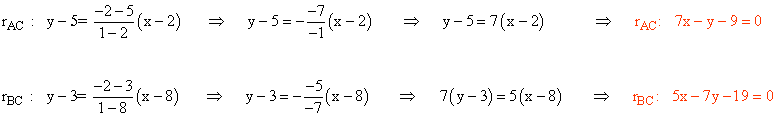
Para calcular las bisectrices utilizamos la siguiente fórmula:
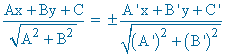
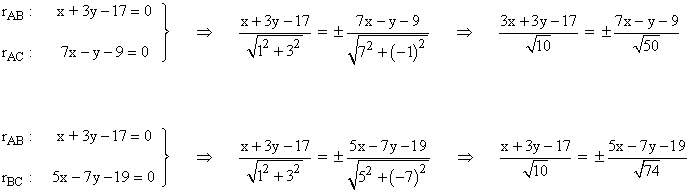
Operando, se obtienen las bisectrices correspondientes:
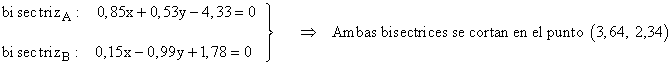
Por lo tanto, el incentro del triángulo ABC es:
![]()
Los centros del triángulo: incentro, baricentro, circuncentro y ortocentro
| Nombre | Dibujo | Elemento |
|---|---|---|
| Triángulo escaleno |
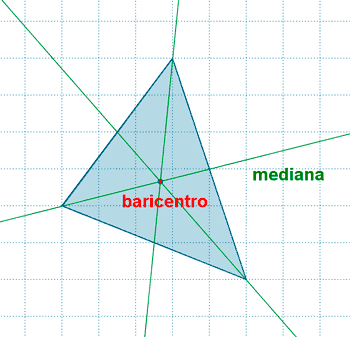 |
Mediana: segmento que une un vértice con el punto medio del lado opuesto Es el centro de gravedad del triángulo. Dista 1/3 del lado y 2/3 del vértice. |
| Triángulo escaleno |
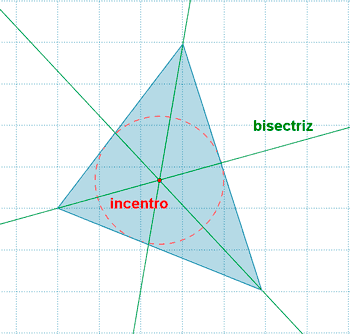 |
Bisectriz: es la recta que divide a un ángulo en dos ángulos iguales Incentro: es el punto de intersección de las bisectrices de cada uno de los ángulos del triángulo |
| Triángulo escaleno | 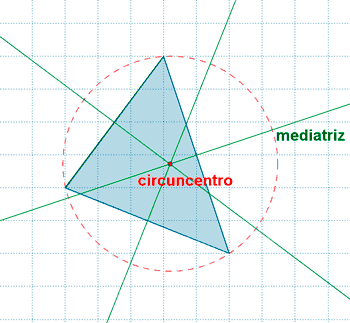 |
Mediatriz: es la recta perpendicular a un lado que pasa por el punto medio del mismo Circuncentro: es el punto de intersección de las mediatrices del triángulo |
| Triángulo acutángulo |
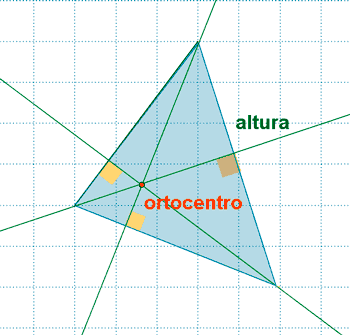 |
Altura: segmento que parte de un vértice y es perpendicular al lado opuesto a dicho vértice Ortocentro: es el punto de intersección de las tres alturas del triángulo |
| Triángulo rectangulo | 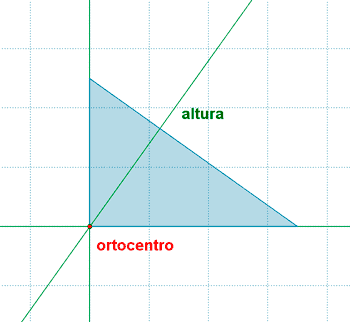 |
En un triángulo rectángulo el ortocentro coincide con el vértice del ángulo recto del triángulo |
| Triángulo obtusángulo | 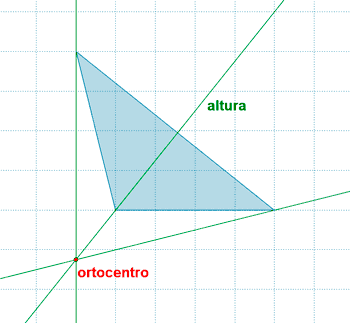 |
En un triángulo obtusángulo el ortocentro queda fuera del triángulo |
| Triángulo equilatero | 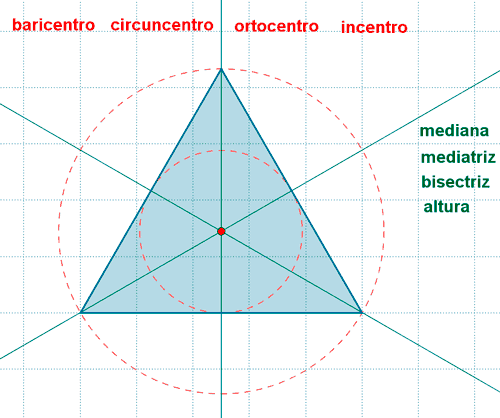 |
En un triángulo equilatero coinciden el baricentro, circuncentro, ortocentro e incentro |
| Recta de Euler | 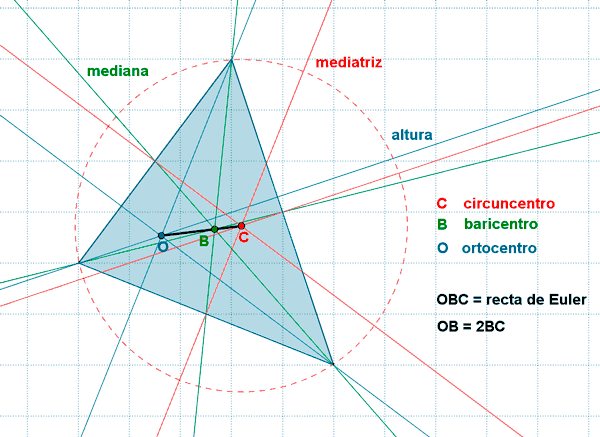 |
|


 INICIO
INICIO