Ecuación punto pendiente, explícita y segmentaria
Ecuación punto pendiente
La ecuación punto pendiente se obtiene a partir de la ecuación continua:
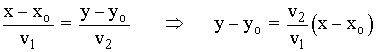
Sabemos que el vector director determina la pendiente de la siguiente forma:
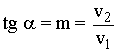
Por tanto, podemos escribir la ecuación:
![]()
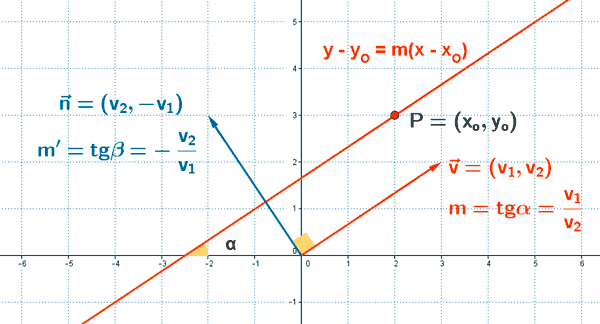
Ecuación explícita (pendiente-ordenada al origen)
La ecuación explícita se obtiene a partir de la ecuación punto pendiente:
![]()
Tomando b = - mxo + yo tenemos que:
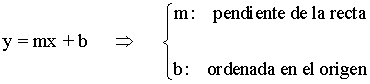
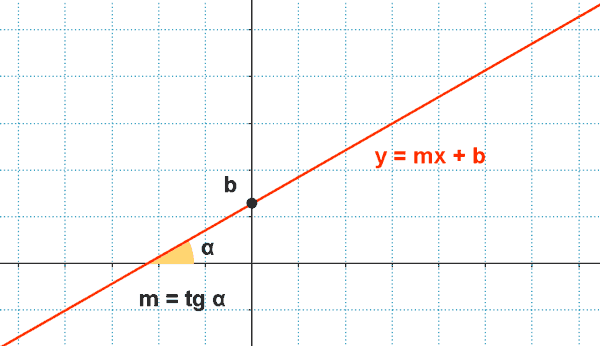
Ecuación de la recta que pasa por dos puntos
La ecuación que pasa por los puntos A(x1, y1) y B(x2, y2) se obtiene a partir de la ecuación pùnto pendiente de la siguiente forma:
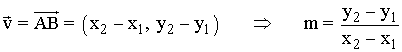
Y aplicamos la fórmula de la ecuación punto pendiente tomando el punto A y la pendiente m :
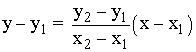
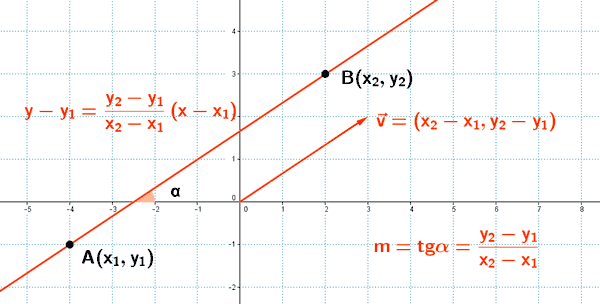
Ejemplos:
1) ¿Cúal es el vector director y la pendiente de las siguientes rectas?

2) ¿Cúal es la pendiente que pasa por los puntos A( 0 , 1 ) y B( 3 , 4 )?

Ecuación canónica o segmentaria
La ecuación canónica o segmentaria se expresa de la siguiente manera:
![]()
donde a es la abscisa en el origen y b la ordenada.
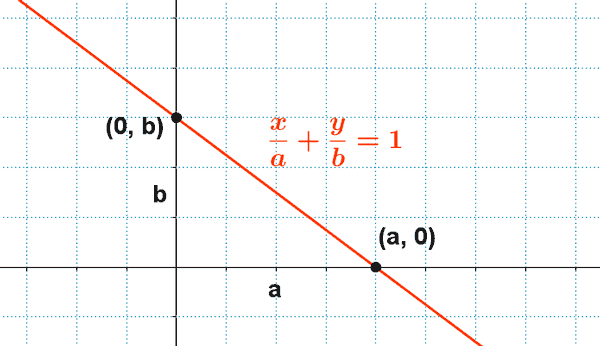
Ejemplos:
1) Hallar todas las formas de la ecuación de la recta cuyos puntos de intersección con los ejes son A(6 , 0) y B(0 , -2 ) .

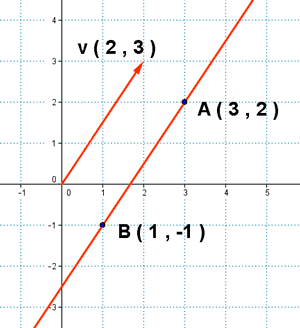
2) Encuentra la ecuación vectorial, paramétrica, continua, general, explicita, punto pendiente y segmenteria de la recta que pasa por los puntos A(3 , 2) y B(1 , -1) .



 INICIO
INICIO

