Ecuación normal de la recta
Vector perpendicular o normal a una recta
Dada la recta r con la ecuación general de la forma Ax + By + C = 0 el vector n(A, B) es un vector normal o perpendicular a la recta r .
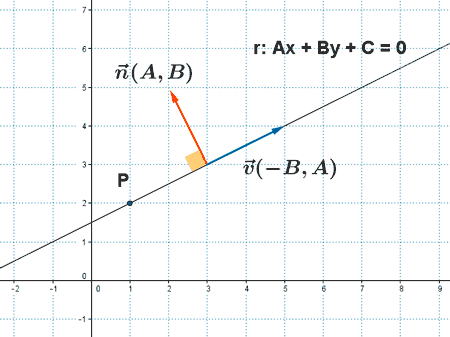
Ejemplo:
Halla un vector normal y otro director de la recta r: x - 2y + 3 = 0
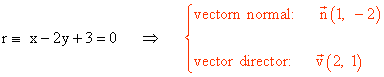
El producto escalar del vector normal y el vector director es 0:
![]()
Ecuación de la recta definida por un punto y un vector normal
Dada la recta r con la ecuación general de la forma Ax + By + C = 0 el vector n(A, B) es un vector normal o perpendicular a la recta r , la ecuación normal de la recta r viene dada por:
![]()
Ejemplo:
Hallar la ecuación general de la recta que contiene al punto (7, 3) y es paralela a la recta que tiene por ecuación 3x + y + 1 = 0 .
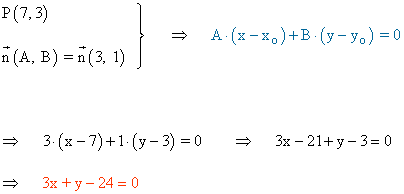
Ecuación normal
La ecuación normal de una recta r en función de los cosenos directores se escribe:
![]()
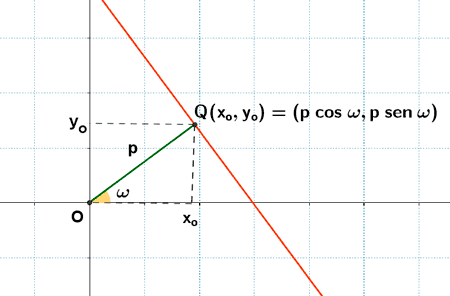
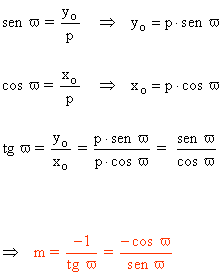
![]()
![]()
Si desarrollamos la expresión de la ecuación normal de la recta y dividimos por el módulo del vector normal n(A, B) :
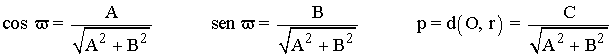
obtenemos la expresión de la ecuación normal:
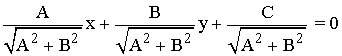
Ejemplo:
1) Dada la ecuación de la recta r : 5x - 7y - 11 = 0 hallar los valores de p y ω y reducirla a su forma normal.
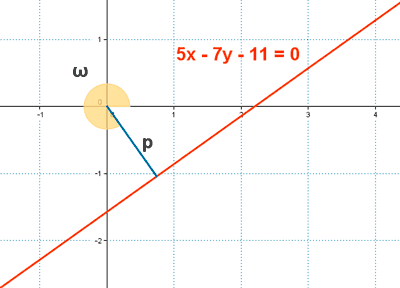
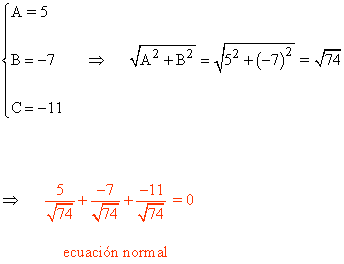
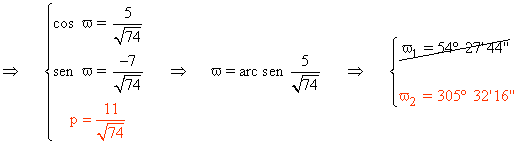
Elegimos ω2 ya que como se observa en el grafico, pertenece al cuarto cuadrante.
2) Hallar los cosenos directores de la recta r : 3x + 4y - 8 = 0
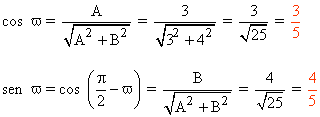
Por lo tanto, la ecuación normal es:
![]()


 INICIO
INICIO

