Problemas resueltos geométricos
1 ) Un triángulo isósceles tiene por lado desigual el segmento que une los puntos A ( 3 , 2 ) y B ( 7 , 4 ). El otro vértice está situado sobre la recta x - y + 4 = 0 . Halla las coordenadas de este vértice y el área del triángulo.
2 ) Los puntos A ( 2 , 4 ) y B ( 5 , 2 ) son vértices de un triángulo rectángulo en A. El tercer vértice C está situado sobre la recta r : x + y - 11 = 0. Determínalo:
3 ) Dados los puntos A(5, 4) , B((7, 3) y C(3, -1) halla el punto D de modo que ABCD sea un paralelogramo. Hallar los ángulos del paralelogramo.
4 ) Un rombo tiene vértice A en el eje de abscisas. Otros dos vértices opuestos son B(3, 1) y D(-5, -3). Hallar A y C .
5 ) Dados los puntos A(2, 1) y B(4, 3) determinar un punto C para que el triángulo ABC sea isósceles y su área sea 4.
6 ) En el triángulo ABC conocemos:
a) El vértice A(-2, 3)
b) La ecuación de la altura que parte del vértice C , hC : 7x - 2y - 11 = 0
c) La ecuación del lado CB , rCB : 2x + y - 11 = 0
Hallar los vértices B y C .
7 ) Comprobar que el cuadrilátero de vértices A(4, 5) , B(9, 0) , C(4, 1) y D(2, 3) es un trapecio rectángulo y halla su área.
8 ) Los puntos A(6, 3) y B(8, 1) son los vértices consecutivos de un rectángulo ABCD . Sabiendo que el vértice C está en la bisectriz del cuarto cuadrante, hallar los vértices C y D y el área del rectángulo .
9 ) Calcula el área del cuadrilátero de vértices A(6, 4) , B(3, -1) , C(-3, -2) y D(-2, 2) .
10 ) Un paralelogramo tiene un vértice en el punto A(7, 5) y dos lados en las rectas 2x - 3y - 15 = 0 y 6x - y - 21 = 0 . Halla los restantes vértices del paralelogramo y su área.
11 ) Un cuadrado tiene dos lados situados sobre las rectas x + y - 5 = 0 y x + y - 9 = 0 . Calcula su área.
12 ) Calcula el área y el perímetro del cuadrilátero que forman las rectas r: 2x + 3y - 6 = 0 y s: 2x + 3y - 12 = 0 con los ejes de coordenadas.
13 ) En el paralelogramo de vértices ABCD se conocen las coordenadas de los puntos A(-3, 1) , B(2, -1) y C(4, 1) . Calcula la medida de sus diagonales y el ángulo que forman.
14 ) Dado el cuadrilátero ABCD cuyos vértices son A(3, 0) , B(1, 4) , C(-4, 3) y D(-2, -2) . Comprobar si es un paralelogramo y determinar de que tipo se trata, hallar su centro y calcular su área.
15 ) Dados los puntos A(6, 0) y B(-6, 0) , obtener un punto C sobre el eje de ordenadas de modo que el triángulo que describan sea equilátero. ¿Existe una única solución? Halla el área de los triángulos resultantes.
16 ) Dado el cuadrilátero de vértices A(2, 2) , B(5, 3) , C(8, -1) y D(2, -3) :
a) Demuestra que se trata de un trapecio
b) Calcula el punto donde se cortan las diagonales
c) Comprueba que la recta que une los puntos medios de los dos lados no paralelos es paralela a las bases del trapecio
17 ) Dado el triángulo de vértices A(-3, 1) , B(-1, 6) y C(6, 2) halla las ecuaciones de las rectas r y s que parten de B y cortan a AC dividiendo al triángulo en tres triángulos de igual área.
18 ) Los puntos A(-2, 3) y B(4, 0) son vértices consecutivos de un paralelogramo que tiene el centro en el origen de coordenadas. Hallar:
a) Los otros dos vértices
b) Los ángulos del paralelogramo
19 ) Tres vértices de un rombo son los puntos A(-4, 2) , B(1, 4) y C(-1, -1) . Halla el cuarto vértice y calcula su su área.
20 ) Dos vértices no consecutivos de un rombo están en los puntos A(-4, 2) y C(-1, -1) y uno de sus lados es paralelo a la recta 5x - 2y - 10 = 0 . Halla las coordenadas de los otros vértices, la longitud de su lado y el área.
21 ) Se considera el cuadrilátero A(-2, 2) , B(6, 4) , C(3, -1) y D(-3, -2) .
a) Calcula la medida de las diagonales
b) Comprueba que los puntos medios de los lados forman un paralelogramo
c) Calcula el perímetro del paralelogramo
d) Comprueba que el perímetro hallado coincide con la suma de las dos diagonales del cuadrilátero original
22 ) Dos vértices consecutivos de un hexágono regular centrado en el origen de coordenadas son A(2, 0) y B(1, √3) . Calcula las coordenadas de los demás vértices.
23 ) Tres vértices consecutivos de un hexágono regular son A(0, 0) , B(4, 0) y C(6, 2√3) . Halla los otros vértices y calcula el área.
1 ) Un triángulo isósceles tiene por lado desigual el segmento que une los puntos A ( 3 , 2 ) y B ( 7 , 4 ). El otro vértice está situado sobre la recta x - y + 4 = 0 . Halla las coordenadas de este vértice y el área del triángulo.

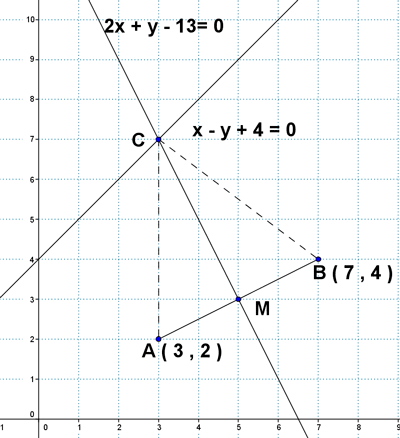

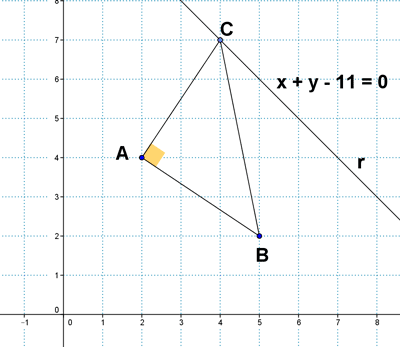
2 ) Los puntos A ( 2 , 4 ) y B ( 5 , 2 ) son vértices de un triángulo rectángulo en A. El tercer vértice C está situado sobre la recta r : x + y - 11 = 0. Determínalo:

3 ) Dados los puntos A(5, 4) , B((7, 3) y C(3, -1) halla el punto D de modo que ABCD sea un paralelogramo. Hallar los ángulos del paralelogramo.
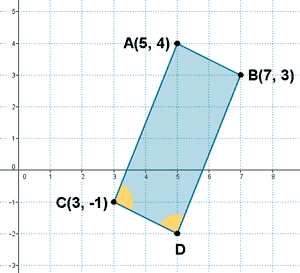
Para que ABCD sea un paralelogramo tiene que darse que:
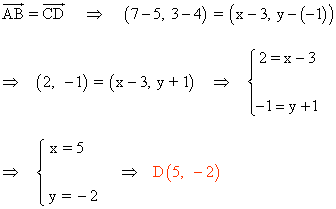
Para calcular los ángulos del paralelogramo utilizamos la siguiente fórmula:
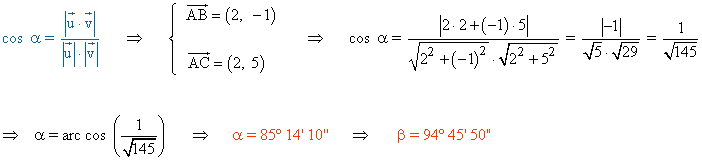
4 ) Un rombo tiene vértice A en el eje de abscisas. Otros dos vértices opuestos son B(3, 1) y D(-5, -3). Hallar A y C .
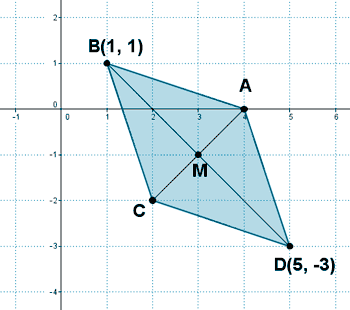
Como es un rombo, sus diagonales se cortan en el mismo punto, es decir, el punto medio del segmento AC es el mismo que el del segmento BD :
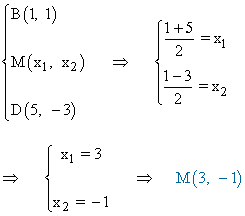
Además, las diagonales son perpendiculares, por lo tanto, calculamos la pendiente del segmento BD :
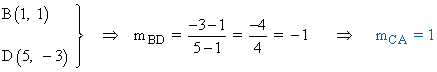
Ahora podemos calcular la recta que pasa por los puntos A y C :
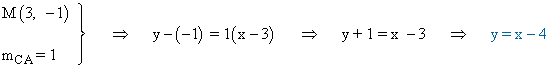
Para conocer el punto A, tenemos que hallar el punto de corte de la recta y = x - 4 con el eje OX :
![]()
Por último, M es el punto medio del segmento AC :
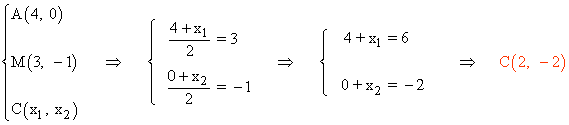
5 ) Dados los puntos A(2, 1) y B(4, 3) determinar un punto C para que el triángulo ABC sea isósceles y su área sea 4.
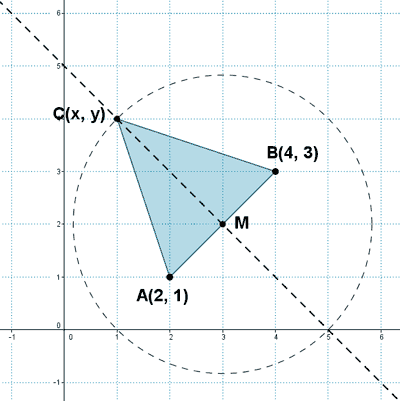
Para que el triángulo sea isósceles, la longitud de los segmentos AC y BD tienen que ser iguales:
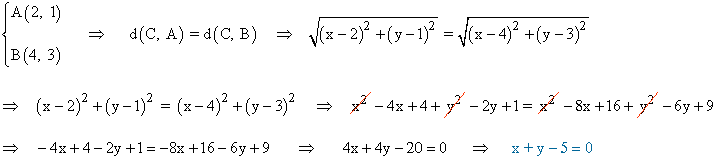
Como el área del triángulo tiene que ser 5:
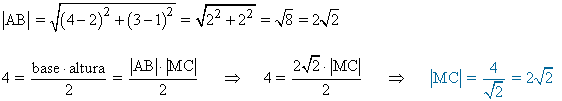
Por lo tanto tenemos dos condiciones para el punto C :
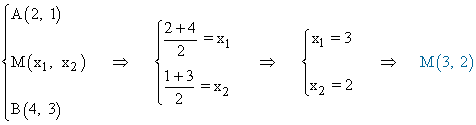
Conociendo el punto M hallamos la condición para la altura del segmento MC :
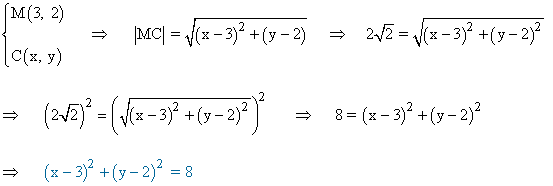
De esta forma, el pnto C queda determinado por la intersección de las siguientes ecuaciones:
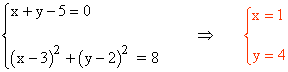
6 ) En el triángulo ABC conocemos:
a) El vértice A(-2, 3)
b) La ecuación de la altura que parte del vértice C , hC : 7x - 2y - 11 = 0
c) La ecuación del lado CB , rCB : 2x + y - 11 = 0
Hallar los vértices B y C .
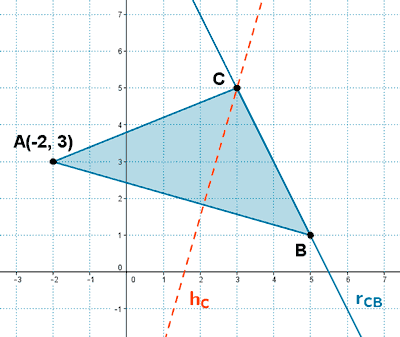
El vértice C es el punto de corte de las rectas:
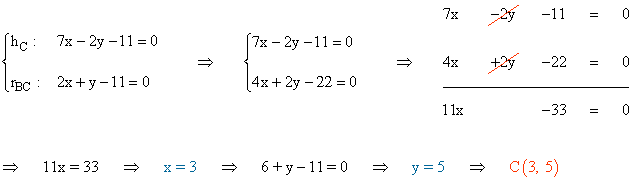
El vértice B es el punto de corte de las rectas que pasan por C y B y por A y B. Como la altura del vértice C es perpendicular a la que pasa por A y B, tenemos que:
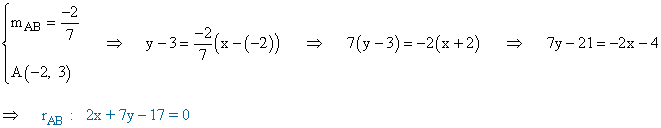
De esta forma, el vértice C queda determinado por la intersección de las siguientes ecuaciones:
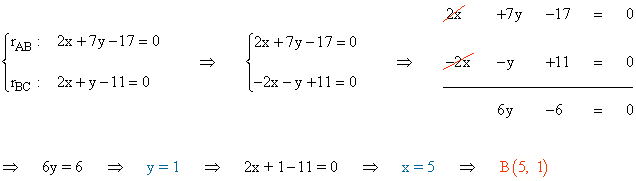
7 ) Comprobar que el cuadrilátero de vértices A(4, 5) , B(9, 0) , C(4, 1) y D(2, 3) es un trapecio rectángulo y halla su área.
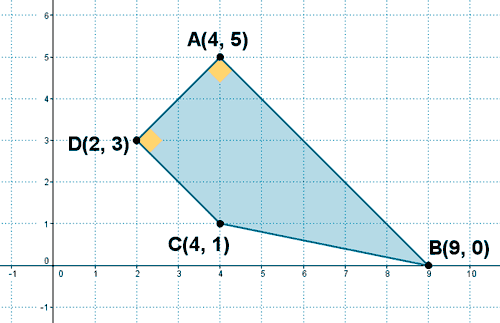
Para ver que es un trapecio rectángulo vemos que los vectores AB y AD y los vectores DA y DC son perpendiculares. Para ello hallamos los vectores, calculamos su producto escalar y comprobamos que valen 0 .
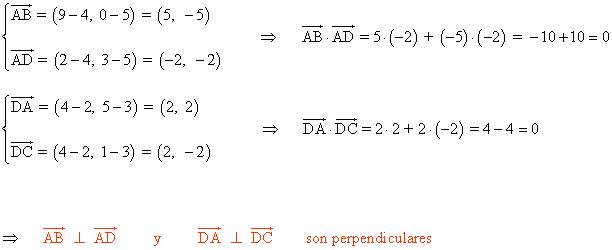
Para hallar el área del trapecio rectángulo utilizamos la siguiente fórmula:
![]()
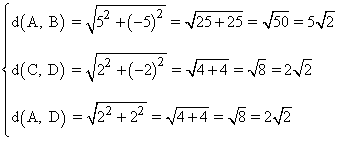
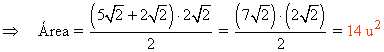
8 ) Los puntos A(6, 3) y B(8, 1) son los vértices consecutivos de un rectángulo ABCD . Sabiendo que el vértice C está en la bisectriz del cuarto cuadrante, hallar los vértices C y D y el área del rectángulo .
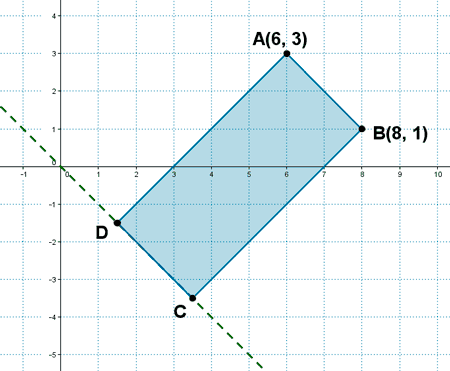
El vértice C está en la intersección de la recta perpendicular a AB y que pasa por B, y la bisectriz del cuarto cuadrante:
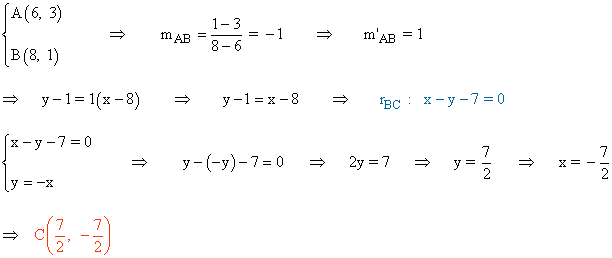
Para calcular D, sabemos que el vector CD es igual al vector BA:
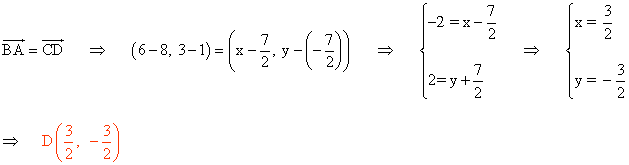
Para calcular el área del rectángulo: Área = base·altura = d(D, C)·d(C, B)
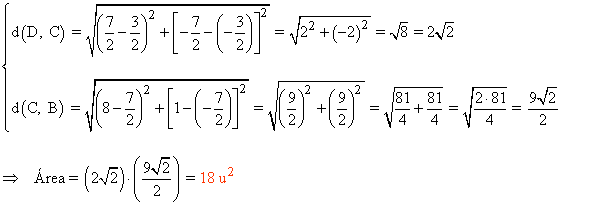
9 ) Calcula el área del cuadrilátero de vértices A(6, 4) , B(3, -1) , C(-3, -2) y D(-2, 2) .
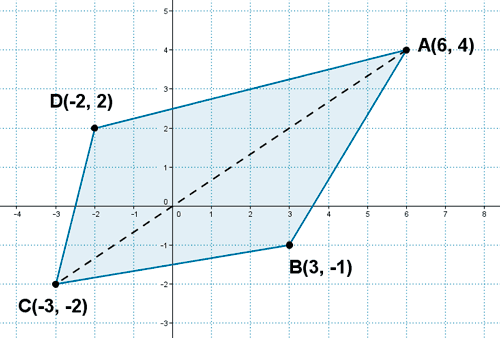
Para calcular el área del cuadrilátero vamos a utilizar la fórmula de Herón:
![]()
Por lo tanto tenemos que calcular cuanto miden cada uno de los segmentos, así como la diagonal del cuadrilátero, es decir, la distancia entre los vértices A y C .
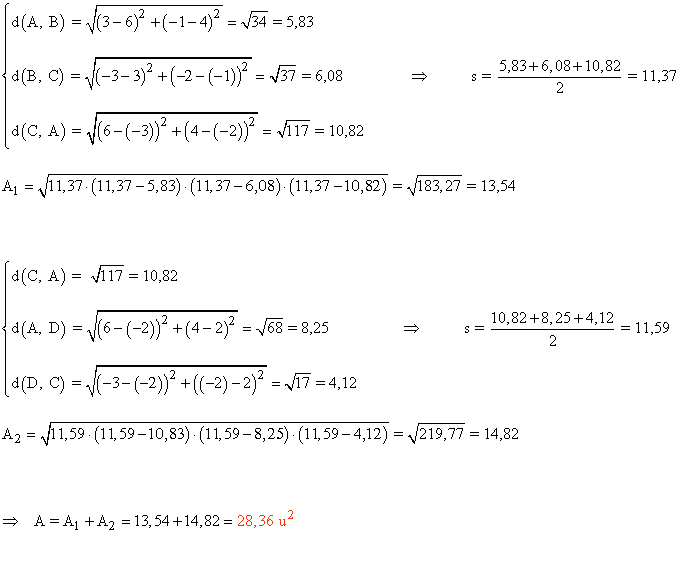
10 ) Un paralelogramo tiene un vértice en el punto A(7, 5) y dos lados en las rectas 2x - 3y - 15 = 0 y 6x - y - 21 = 0 . Halla los restantes vértices del paralelogramo y su área.
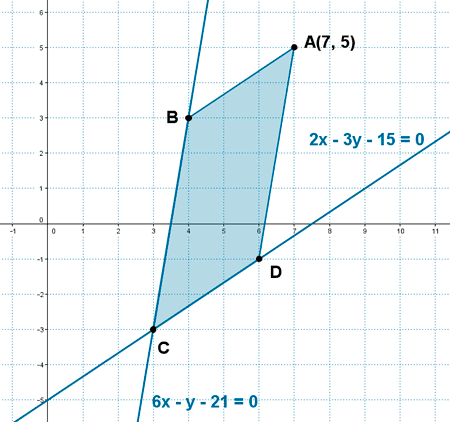
El vértice D es el punto en el cual se corta la recta paralela a 6x - y - 21 = 0 y que pasa por el punto A :
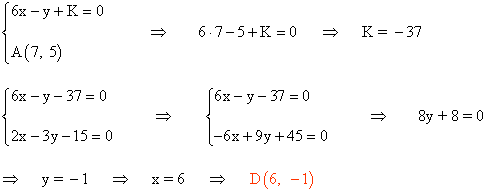
El vértice B es el punto en el cual se corta la recta paralela a 2x - 3y - 15 = 0 y que pasa por el punto A :
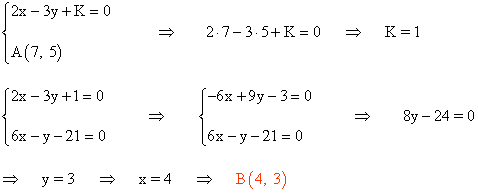
El vértice C es el punto donde se cortan ambas rectas::
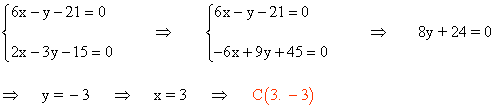
Para comprobar si el paralelogramo es rectángulo o no, calculamos el producto escalar de los vectores CB y CD :
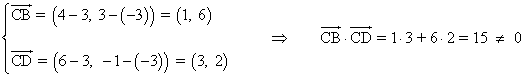
Como el producto escalar es distinto de 0, no es un paralelogramo rectángulo, por lo tanto tenemos que hallar la altura, la cuál se calcula entre la distancia de un vértice y su recta opuesta:
![]()
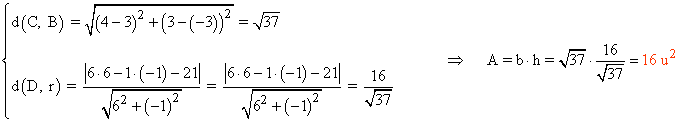
11 ) Un cuadrado tiene dos lados situados sobre las rectas x + y - 5 = 0 y x + y - 9 = 0 . Calcula su área.
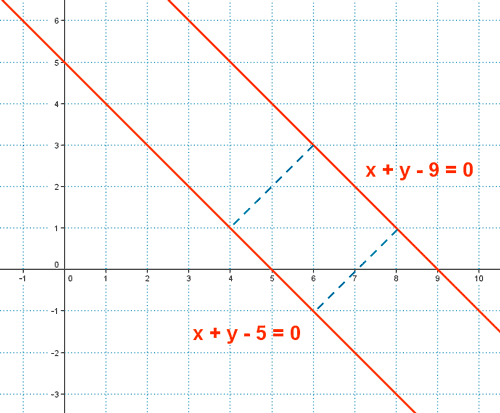
Simplemente tenemos que calcular la distancia entre ambas rectas, las cuales son paralelas. Dicha distancia es el lado del cuadrado:
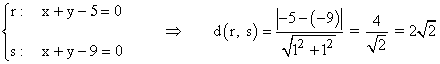
Aplicamos el área de un cuadrado: A = L2
![]()
12 ) Calcula el área y el perímetro del cuadrilátero que forman las rectas r: 2x + 3y - 6 = 0 y s: 2x + 3y - 12 = 0 con los ejes de coordenadas.
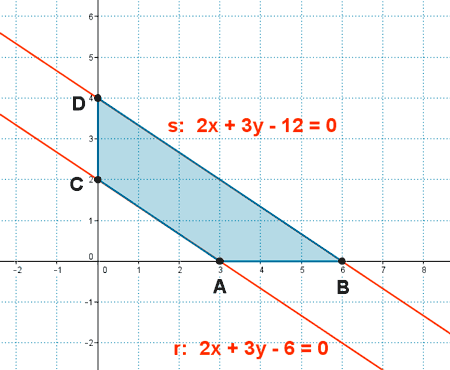
Calculamos los puntos de corte de ambas rectas con los ejes de coordenadas:
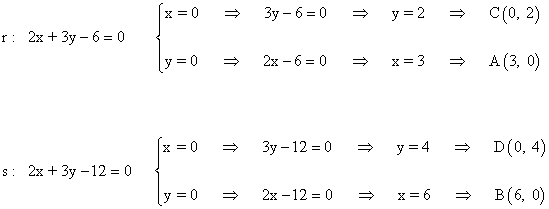
Para calcular el perímetro se hallan las distancias entre los vértices que conforman el cuadrilátero:
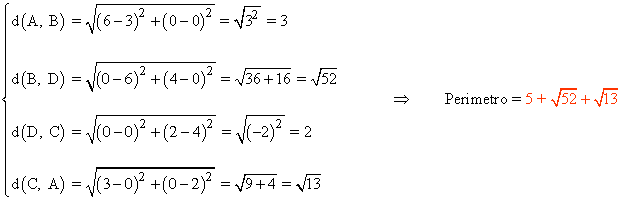
Para calcular el área restamos el área del triángulo OAC a la del triángulo OBD:
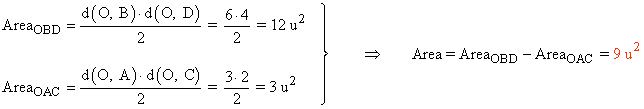
13 ) En el paralelogramo de vértices ABCD se conocen las coordenadas de los puntos A(-3, 1) , B(2, -1) y C(4, 1) . Calcula la medida de sus diagonales y el ángulo que forman.
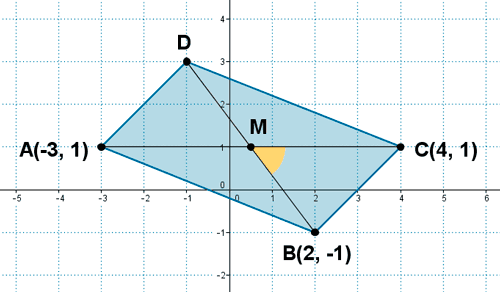
En un paralelogramo sus diagonales se cortan en el mismo punto, es decir, el punto medio del segmento AC es el mismo que el del segmento BD :
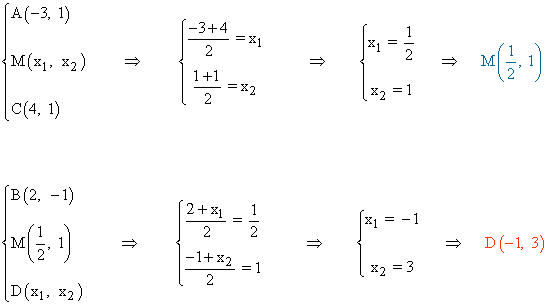
Para calcular el ángulo que forman las diagonales utilizamos los vectores AC y DB :
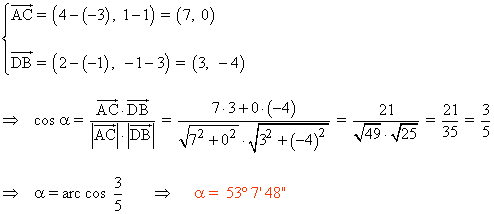
14 ) Dado el cuadrilátero ABCD cuyos vértices son A(3, 0) , B(1, 4) , C(-4, 3) y D(-2, -2) . Comprobar si es un paralelogramo y determinar de que tipo se trata, hallar su centro y calcular su área.
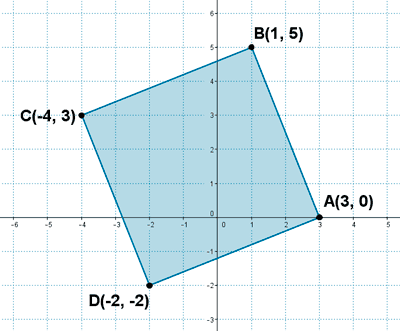
Comprobamos que se trata de un paralelogramo viendo que las longitudes de sus lados opuestos son iguales:
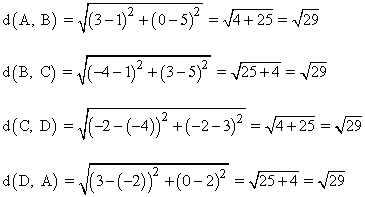
Es decir, se trata de un paralelogramo ya que sus cuatro lados son iguales. Tenemos que determinar que tipo de paralelogramo es, un cuadrado o un rombo. Comprobamos las pendientes de dos lados contiguos:
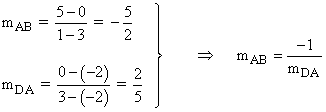
Es decir, ambas pendientes son inversas y cambiadas de signo, por lo tanto son perpendiculares. Es un cuadrado.
También se puede comprobar con el producto escalar de los vectores AB y AD :
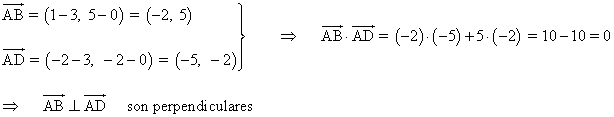
Para hallar el centro calculamos el punto medio de cualquiera de sus diagonales, por ejemplo, el segmento CA :
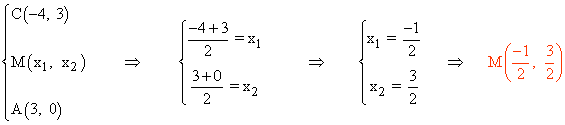
Por último hallamos el área del cuadrado:
![]()
15 ) Dados los puntos A(6, 0) y B(-6, 0) , obtener un punto C sobre el eje de ordenadas de modo que el triángulo que describan sea equilátero. ¿Existe una única solución? Halla el área de los triángulos resultantes.
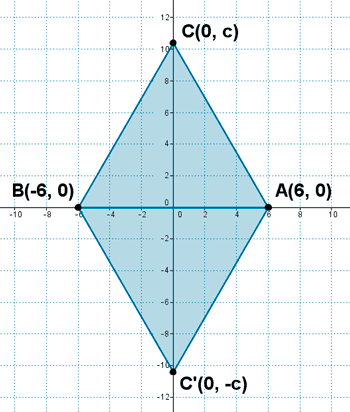
Los vectores formados por los vértices tienen que tener la misma longitud, por lo tanto:
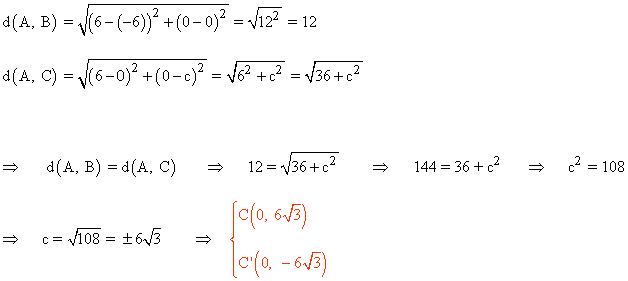
Es decir, existen dos soluciones. Por último calculamos el área:
![]()
16 ) Dado el cuadrilátero de vértices A(2, 2) , B(5, 3) , C(8, -1) y D(2, -3) :
a) Demuestra que se trata de un trapecio
b) Calcula el punto donde se cortan las diagonales
c) Comprueba que la recta que une los puntos medios de los dos lados no paralelos es paralela a las bases del trapecio
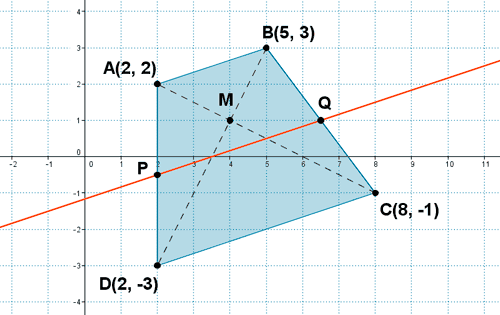
(a)
Los lados AB y DC son paralelos ya que los vectores son proporcionales:
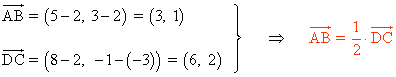
(b)
Para calcular el punto de corte de las diagonales tenemos que hallar las rectas que contienen a las diagonales:
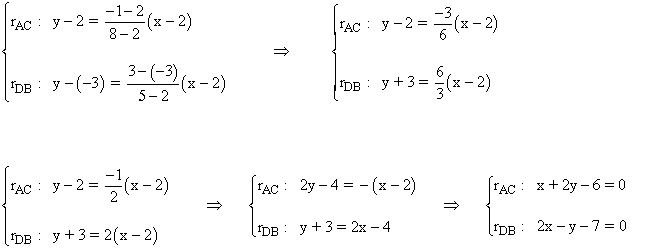
Resolvemos el sistema para hallar el punto de corte:
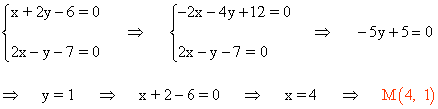
(c)
Los puntos medios de los segmentos AD y BC son:
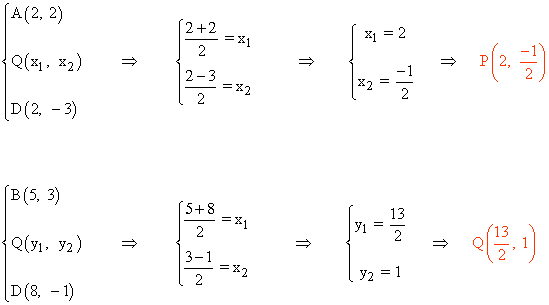
Calculamos las coordenadas del vector PQ y comprobamos que es proporcional a los vectores AB y DC :
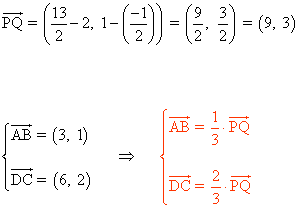
17 ) Dado el triángulo de vértices A(-3, 1) , B(-1, 6) y C(6, 2) halla las ecuaciones de las rectas r y s que parten de B y cortan a AC dividiendo al triángulo en tres triángulos de igual área.
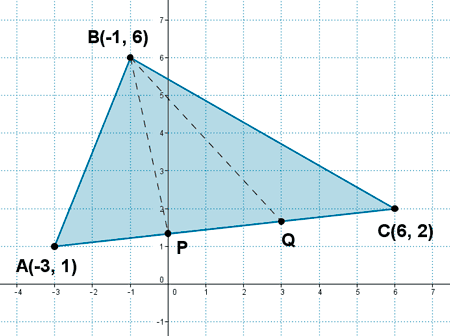
Para calcular las rectas, dividimos el segmento AC en tres partes iguales, es decir:
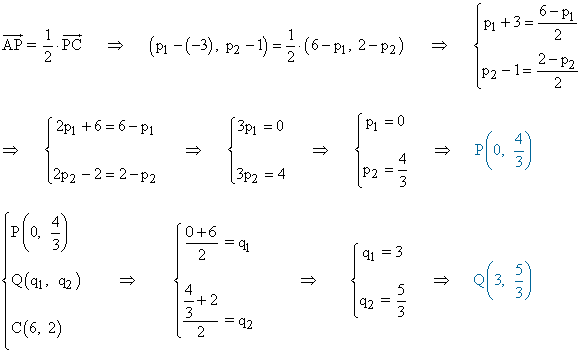
Ya solamente tenemos que calcular las rectas que pasan por los puntos B y P y B y Q :
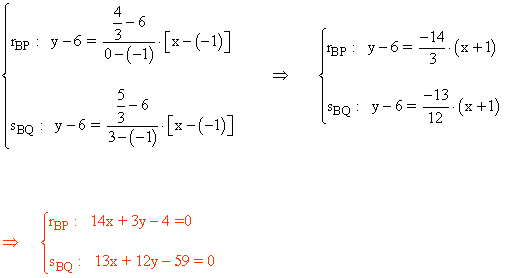
18 ) Los puntos A(-2, 3) y B(4, 0) son vértices consecutivos de un paralelogramo que tiene el centro en el origen de coordenadas. Hallar:
a) Los otros dos vértices
b) Los ángulos del paralelogramo
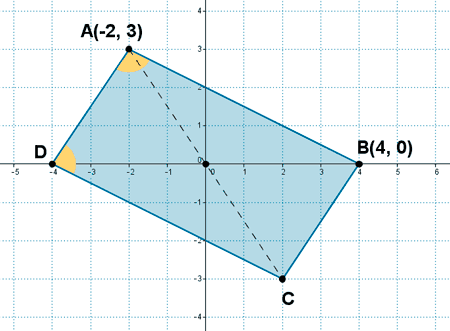
(a)
El centro del paralelogramo es el punto medio de los segmentos AC y DB :
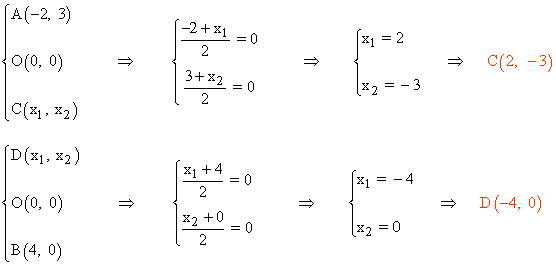
(b)
Para calcular los ángulos del paralelogramo utilizamos los vectores DA y DC :
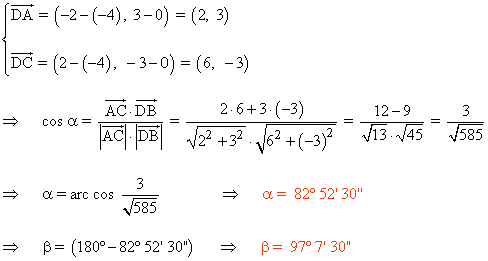
19 ) Tres vértices de un rombo son los puntos A(-4, 2) , B(1, 4) y C(-1, -1) . Halla el cuarto vértice y calcula su su área.
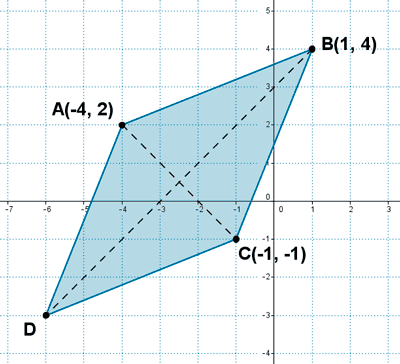
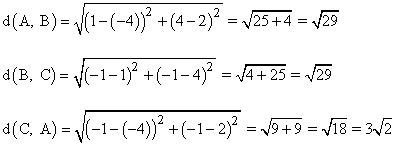
Por lo tanto, los vértices A y B y los vértices B y C son consecutivos ya que tienen la misma longitud, mientras que los vértices A y C forman una de las diagonales.
Al tratarse de un rombo, es decir, un paralelogramo, tienen que coincidir los vectores DA y CB :
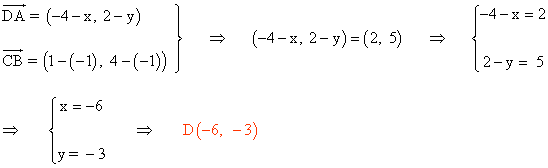
Para calcular el área necesitamos calcular cuanto miden las dos diagonales del rombo:
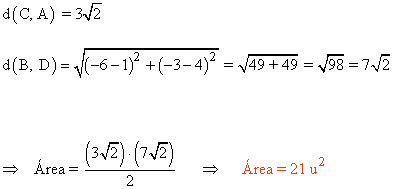
20 ) Dos vértices no consecutivos de un rombo están en los puntos A(-4, 2) y C(-1, -1) y uno de sus lados es paralelo a la recta 5x - 2y - 10 = 0 . Halla las coordenadas de los otros vértices, la longitud de su lado y el área.
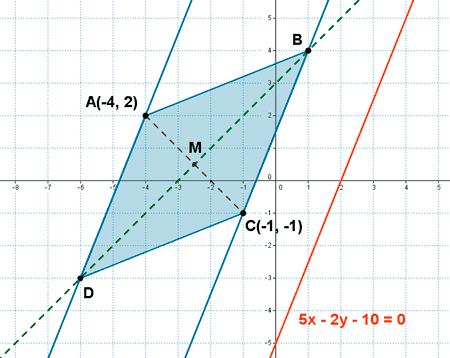
En primer lugar calculamos las rectas paralelas a 5x - 2y - 10 = 0 que pasan por los puntos A(-4, 2) y C(-1, -1) :
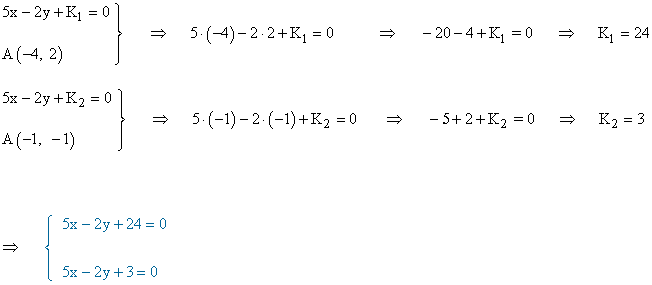
Para calcular los vértices que faltan, necesitamos hallar la mediatriz del segmento AC , por lo tanto tenemos que calcular la pendiente del vector normal a AC y su punto medio:
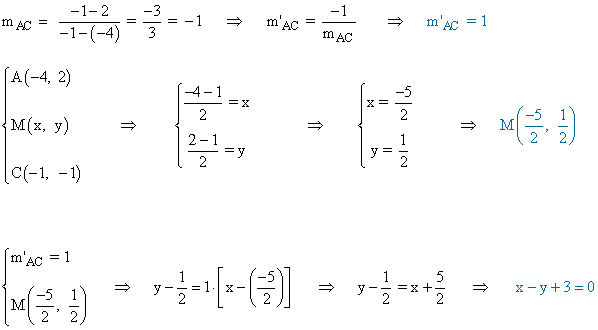
Los vértices que faltan del rombo son los puntos de intersección de la mediatriz del segmento AC con las dos rectas paralelas calculadas anteriormente:
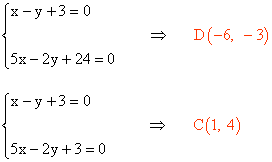
La longitud de su lado es la distancia entre dos vértices consecutivos:
![]()
Para calcular el área necesitamos calcular cuanto miden las dos diagonales del rombo:
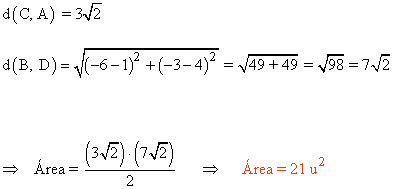
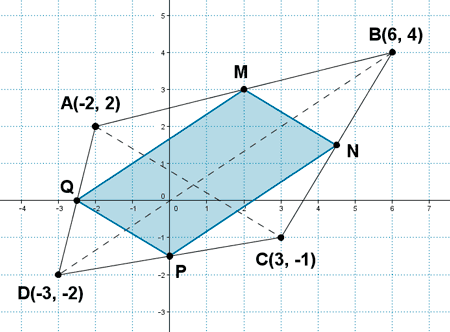
21 ) Se considera el cuadrilátero A(-2, 2) , B(6, 4) , C(3, -1) y D(-3, -2) .
a) Calcula la medida de las diagonales
b) Comprueba que los puntos medios de los lados forman un paralelogramo
c) Calcula el perímetro del paralelogramo
d) Comprueba que el perímetro hallado coincide con la suma de las dos diagonales del cuadrilátero original
(a)
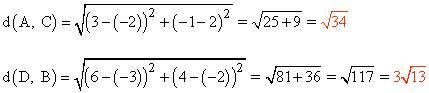
(b)
Calculamos los puntos medios de cada uno de los lados:
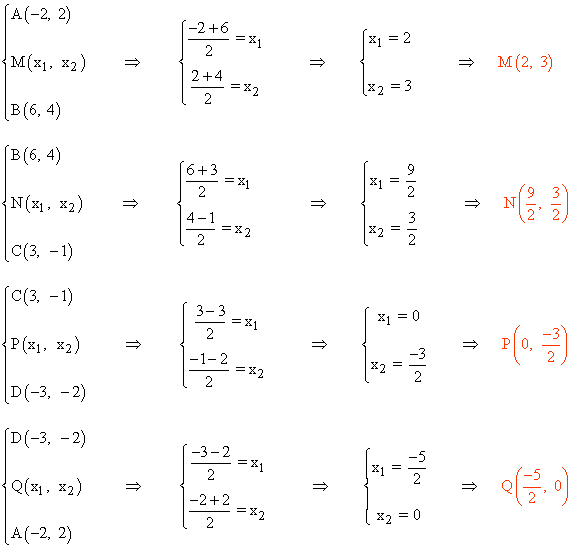
Comprobamos que se trata de un paralelogramo viendo que los vectores MN y QP y QM y PN coinciden:
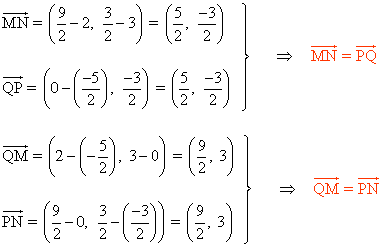
Otra forma de comprobarlo es calculando los puntos medios de las diagonales del cuadrilátero MNPQ :
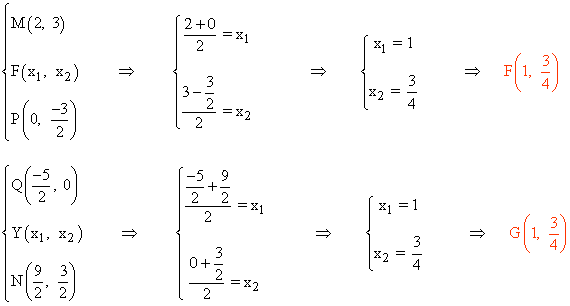
Como sus puntos medios coinciden, se trata de un paralelogramo.
Se verifica la propiedad de que los puntos medios de los lados de cualquier cuadrilátero son los vértices de un paralelogramo.
(c)
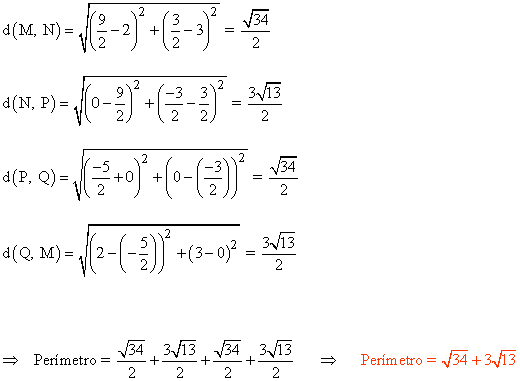
(d)
El perímetro del paralelogramo coincide con la suma de las dos diagonales del cuadrilátero original.
22 ) Dos vértices consecutivos de un hexágono regular centrado en el origen de coordenadas son A(2, 0) y B(1, √3) . Calcula las coordenadas de los demás vértices.
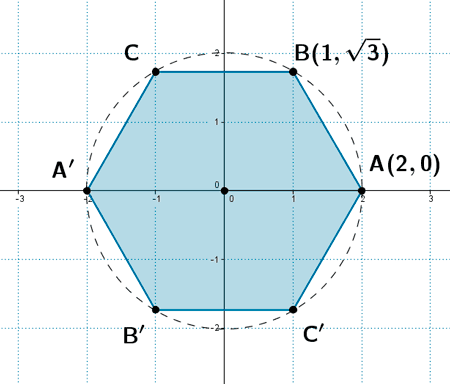
Calculamos los vértices A' (x1, y1) y B' (x2, y2) que son simétricos de A y B respecto del origen de coordenadas, es decir, el punto (0, 0) es el punto medio de los segmentos AA' y BB' :
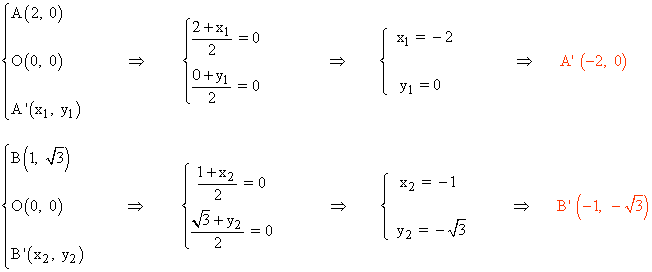
En un hexágono regular el lado coincide con el radio de la circunferencia donde está inscrito, por lo tanto el vértice C se obtiene al aplicar el vector (-2, 0) al punto B y el vértice C' al aplicar el vector (2, 0) al punto B' :
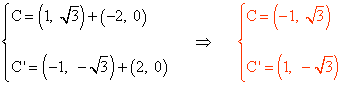
23 ) Tres vértices consecutivos de un hexágono regular son A(0, 0) , B(4, 0) y C(6, 2√3) . Halla los otros vértices y calcula el área.
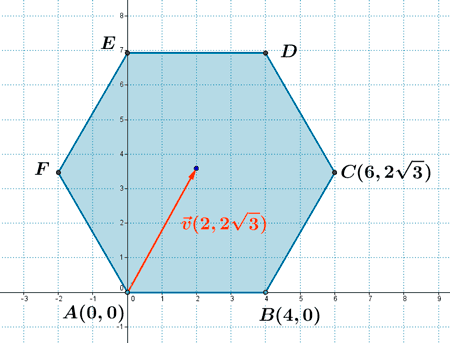
Conocido el vector director, podemos calcular los vertices consecutivos de la siguiente manera:
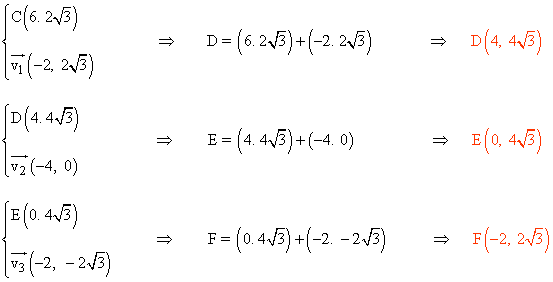
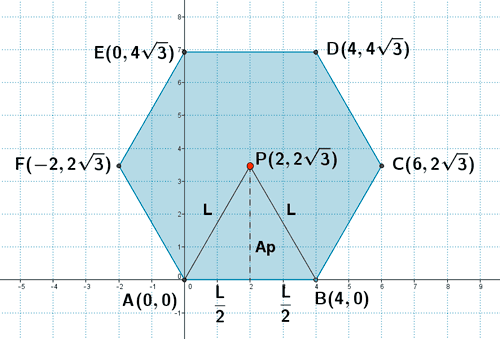
El centro del hexágono corresponde con el punto medio del segmento AD :
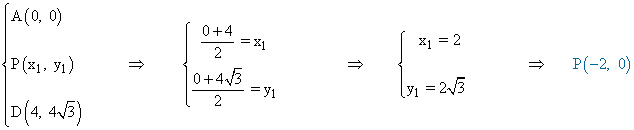
Por otro lado, hallamos la apotema, siendo esta la distancia del punto P al eje OX :
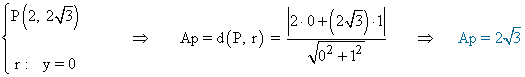
En último lugar calculamos el lado del hexágono como la distancia entre A y B :
![]()
Para calcular el área primero hallamos el perímetro:
![]()


 INICIO
INICIO