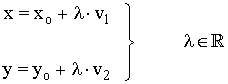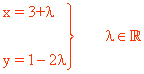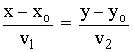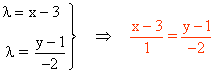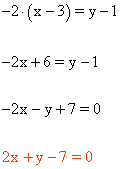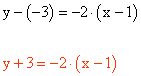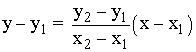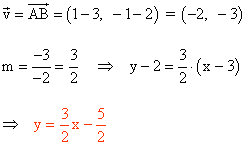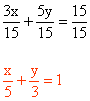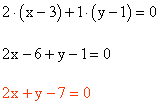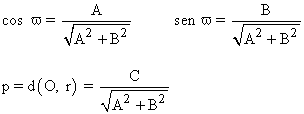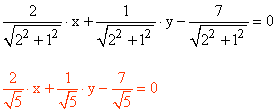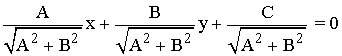Ejercicios resueltos de tipos de ecuaciones de rectas.
Vector director y pendiente.
1 ) Indica un punto y un vector de las siguientes rectas:
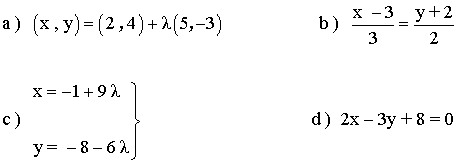
2 ) Calcular la pendiente de las siguientes rectas:

3-a ) Escribe las ecuaciones generales de los ejes coordenados. ¿ Cúal es la ecuación paramétrica de cada uno ?
3-b ) Escribe la ecuación paramétrica y explícita de la bisectriz del primer y tercer cuadrante. Escribe también la de la bisectriz del segundo y cuarto cuadrante
4-a ) Dibuja la recta que pasa por el punto A ( -1 , 2 ) y que tiene de pendiente -3/5. Halla la ecuación de dicha recta.
4-b ) Hallar y representar la recta que pasa por los puntos A ( 2 , 1 ) y B ( 3 , 4 )
5 ) Calcula la ecuación vectorial y las ecuaciones paramétricas de cada una de las siguientes rectas:
a ) La recta que pasa por el punto P ( 3 , 3 ) y lleva la dirección del vector u ( 2 , 1 ).
b ) La recta que pasa por los puntos A ( 2 , -1 ) y B ( 3 , 4 ).
c ) La recta que tiene como uno de sus vectores de dirección el u ( -1 , 2 ) y corta a la parte positiva del eje de abcisas en un punto que dista 2 unidades del origen de coordenadas.
d ) La recta que tiene como vector director U ( 1 , -4 ) y corta a la parte negativa del eje de abcisas en un punto que dista 5 unidades del origen de coordenadas.
e ) La recta que tiene por dirección la del vector u ( 5 , 6 ) y corta al eje de ordenadas en un punto que dista 1 unidad negativa del origen de coordenadas.
6 ) Representa y halla las distintas ecuaciones de la recta que pasa por el punto A ( 3 , 1 ) y tiene como vector director v ( 1 , -2 )
7 ) Encuentra la ecuación vectorial, paramétrica, continua, general, explicita, punto pendiente y segmentaria de la recta que pasa por los puntos A ( 3 , 2 ) y B ( 1 , -1)
8 ) Dada la recta r : x + 3y + 2 = 0 en forma general, escribirla en forma explícita, canónica, normal, continua y vectorial.
9 ) Dada la recta 3x + 2y = 4, ¿ qué tipo de ecuación es ? Hallar un punto, un vector normal, un vector director y la pendiente. Realizar también la representación gráfica.
10 ) ¿ Cúal es la ecuación paramétrica de la recta que pasa por los puntos A ( 2 , 1 ) y B ( 1 , -2 ) ? ¿ Para qué valores del parámetro se obtienen los puntos P y Q y el punto medio de P y Q ?
11 ) Calcular:
a ) ¿ Cúal es la pendiente de la recta que pasa por los puntos A ( 2 , 2 ) y B ( 0 , 4 ) ?
b ) La ecuación explicita e implicita o general de la recta que pasa por los puntos P ( 1 , 4 ) y Q ( 2 , 3 )
12 ) Hallar todas las formas de la ecuación de la recta cuyos puntos de intersección con los ejes son A = ( 6 , 0 ) y B = ( 0 , -2 )
13 ) Escribe en forma explícita y continua la ecuación de la recta 2x + 3y = 6
14-a ) Determinar si los puntos A ( 3 , 1 ) B ( 5 , 2 ) C ( 1 , 0 ) están alineados. En caso afirmativo, escribe la ecuación de la recta que los contiene.
14-b ) Verifica si los puntos ( 2 , 1 ) , ( 1 , 5 ) y ( 12 , 3 ) están alineados. En caso afirmativo, escribe la ecuación de la recta.
15-a ) ¿ Pertenece el punto P = ( 3 , 3 ) a la recta que pasa por los puntos A = ( 1 , -1 ) y B ( 2 , 1 ) ?
15-b ) ¿ Pertenece el punto P ( 0 , 5 ) a la recta determinada por el vector ( 1 , 3 ) y el punto ( 2 , 3 ) ?
16 ) Escribe en la forma normal las rectas r : 4x + 3y - 10 = 0 y s : √3x - y + 4 = 0
17-a ) ¿ Cúal es la pendiente que pasa por los puntos A ( 0 , 1 ) y B ( 3 , 4 ) ?
17-b ) ¿ Cúal es el vector dirección y la pendiente de las siguientes rectas ?
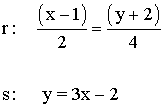
18 ) Calcula la recta que pasa por el punto A ( 2 , 5 ) y forma con el eje de abcisas un ángulo de 30º. Expicar los pasos a seguir.
19-a ) Halla un vector normal y otro director de la recta r: x - 2y + 3 = 0
19-b ) Hallar la ecuación general de la recta que contiene al punto (7, 3) y es paralela a la recta que tiene por ecuación 3x + y + 1 = 0 .
20-a ) Dada la ecuación de la recta r : 5x - 7y - 11 = 0 hallar los valores de p y ω y reducirla a su forma normal.
20-b ) Hallar los cosenos directores de la recta r : 3x + 4y - 8 = 0
21 ) Resumen de tipos de ecuaciones de rectas
1 ) Indica un punto y un vector de las siguientes rectas:
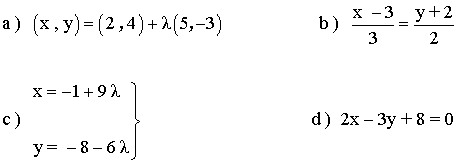
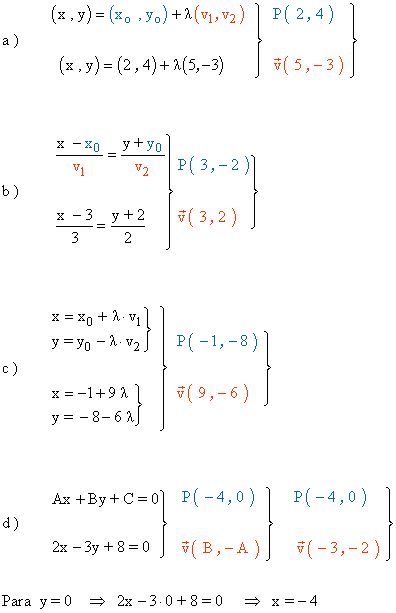
2 ) Calcular la pendiente de las siguientes rectas:

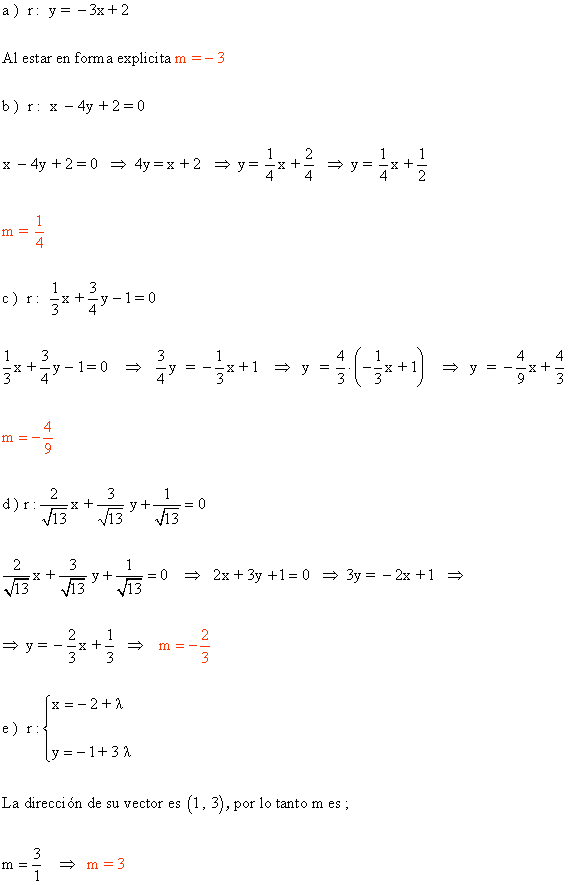

3-a ) Escribe las ecuaciones generales de los ejes coordenados. ¿ Cúal es la ecuación paramétrica de cada uno ?
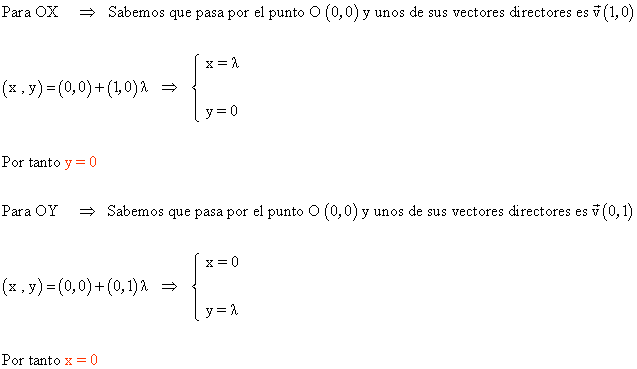
3-b ) Escribe la ecuación paramétrica y explícita de la bisectriz del primer y tercer cuadrante. Escribe también la de la bisectriz del segundo y cuarto cuadrante

4-a ) Dibuja la recta que pasa por el punto A ( -1 , 2 ) y que tiene de pendiente -3/5. Halla la ecuación de dicha recta.
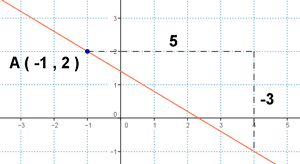

4-b ) Hallar y representar la recta que pasa por los puntos A ( 2 , 1 ) y B ( 3 , 4 )

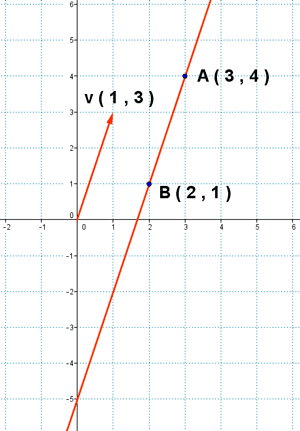
5 ) Calcula la ecuación vectorial y las ecuaciones paramétricas de cada una de las siguientes rectas:
a ) La recta que pasa por el punto P ( 3 , 3 ) y lleva la dirección del vector u ( 2 , 1 ).
b ) La recta que pasa por los puntos A ( 2 , -1 ) y B ( 3 , 4 ).
c ) La recta que tiene como uno de sus vectores de dirección el u ( -1 , 2 ) y corta a la parte positiva del eje de abcisas en un punto que dista 2 unidades del origen de coordenadas.
d ) La recta que tiene como vector director U ( 1 , -4 ) y corta a la parte negativa del eje de abcisas en un punto que dista 5 unidades del origen de coordenadas.
e ) La recta que tiene por dirección la del vector u ( 5 , 6 ) y corta al eje de ordenadas en un punto que dista 1 unidad negativa del origen de coordenadas.
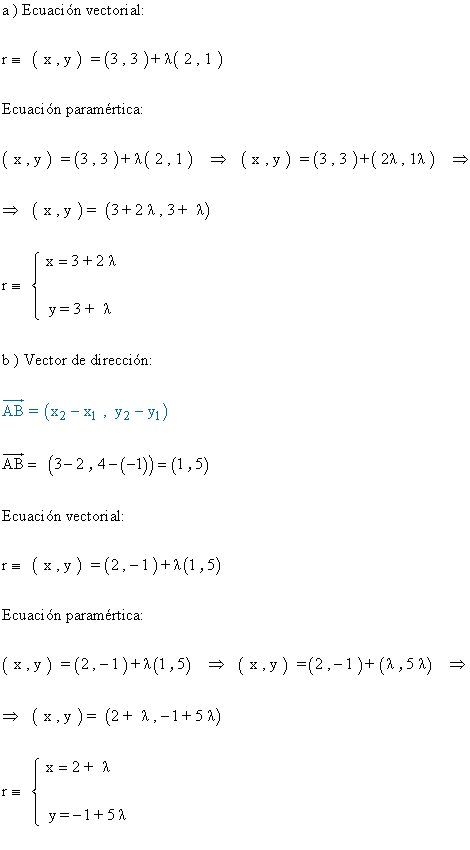


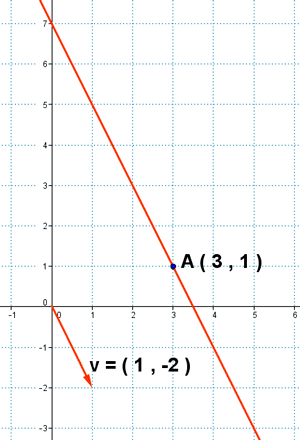
6 ) Representa y halla las distintas ecuaciones de la recta que pasa por el punto A ( 3 , 1 ) y tiene como vector director v ( 1 , -2 )

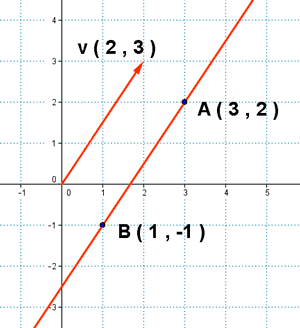
7 ) Encuentra la ecuación vectorial, paramétrica, continua, general, explicita, punto pendiente y segmenteria de la recta que pasa por los puntos A ( 3 , 2 ) y B ( 1 , -1)

8 ) Dada la recta r : x + 3y + 2 = 0 en forma general, escribirla en forma explícita, canónica, normal, continua y vectorial.
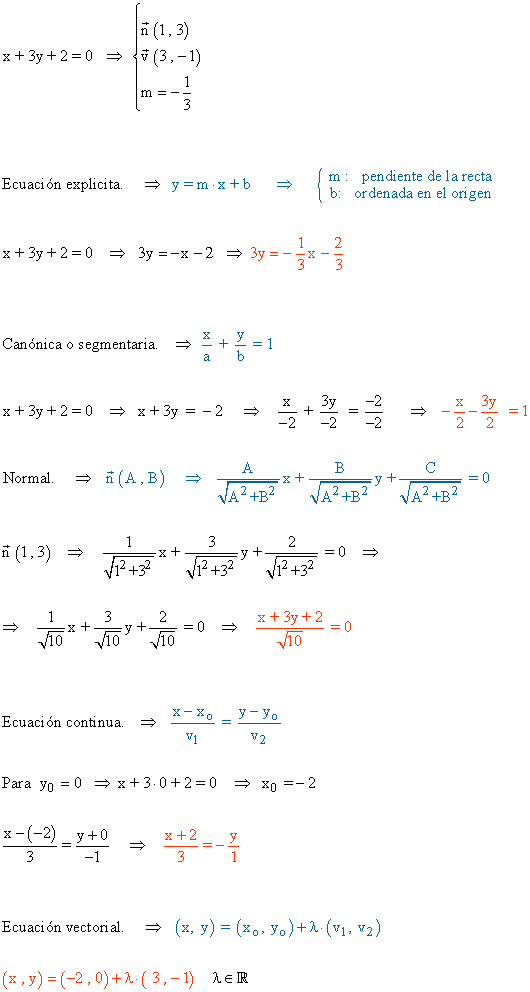
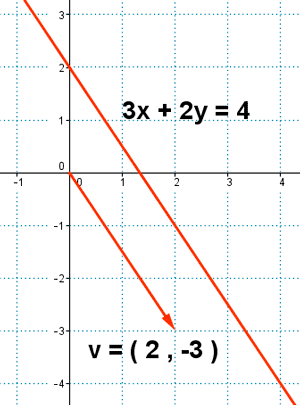
9 ) Dada la recta 3x + 2y = 4, ¿ qué tipo de ecuación es ? Hallar un punto, un vector normal, un vector director y la pendiente. Realizar también la representación gráfica.

10 ) ¿ Cúal es la ecuación paramétrica de la recta que pasa por los puntos A ( 2 , 1 ) y B ( 1 , -2 ) ? ¿ Para qué valores del parámetro se obtienen los puntos P y Q y el punto medio de P y Q ?

11 ) Calcular:
a ) ¿ Cúal es la pendiente de la recta que pasa por los puntos A ( 2 , 2 ) y B ( 0 , 4 ) ?
b ) La ecuación explicita e implicita o general de la recta que pasa por los puntos P ( 1 , 4 ) y Q ( 2 , 3 )


12 ) Hallar todas las formas de la ecuación de la recta cuyos puntos de intersección con los ejes son A = ( 6 , 0 ) y B = ( 0 , -2 )

13 ) Escribe en forma explícita y continua la ecuación de la recta 2x + 3y = 6
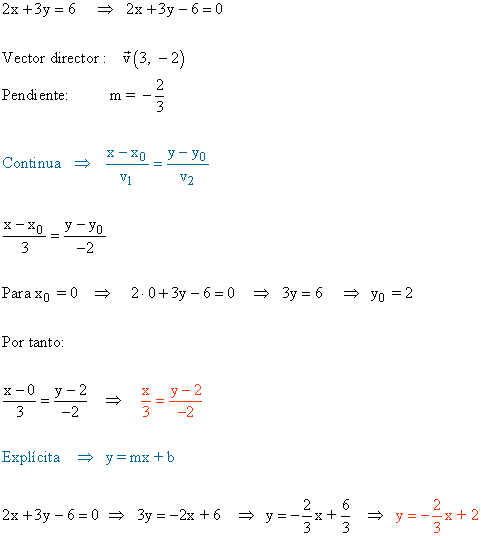
14-a ) Determinar si los puntos A ( 3 , 1 ) B ( 5 , 2 ) C ( 1 , 0 ) están alineados. En caso afirmativo, escribe la ecuación de la recta que los contiene.

14-b ) Verifica si los puntos ( 2 , 1 ) , ( 1 , 5 ) y ( 12 , 3 ) están alineados. En caso afirmativo, escribe la ecuación de la recta.

15-a ) ¿ Pertenece el punto P = ( 3 , 3 ) a la recta que pasa por los puntos A = ( 1 , -1 ) y B ( 2 , 1 ) ?

15-b ) ¿ Pertenece el punto P ( 0 , 5 ) a la recta determinada por el vector ( 1 , 3 ) y el punto ( 2 , 3 ) ?

16 ) Escribe en la forma normal las rectas r : 4x + 3y - 10 = 0 y s : √3x - y + 4 = 0
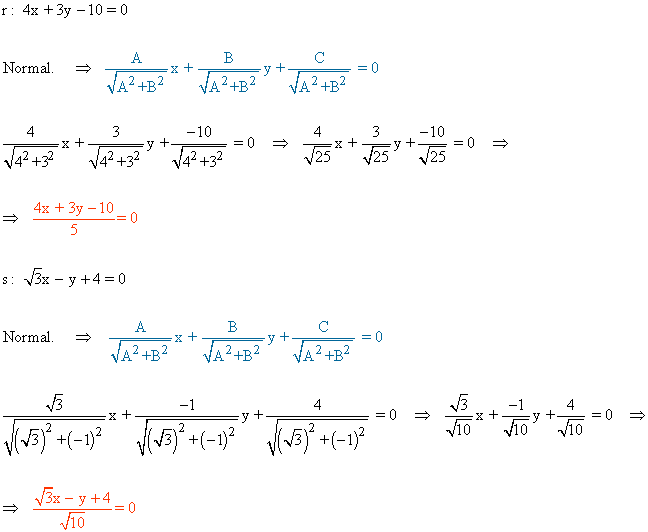
17-a ) ¿ Cúal es la pendiente que pasa por los puntos A ( 0 , 1 ) y B ( 3 , 4 ) ?

17-b ) ¿ Cúal es el vector dirección y la pendiente de las siguientes rectas ?
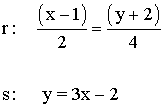

18 ) Calcula la recta que pasa por el punto A ( 2 , 5 ) y forma con el eje de abcisas un ángulo de 30º. Expicar los pasos a seguir.
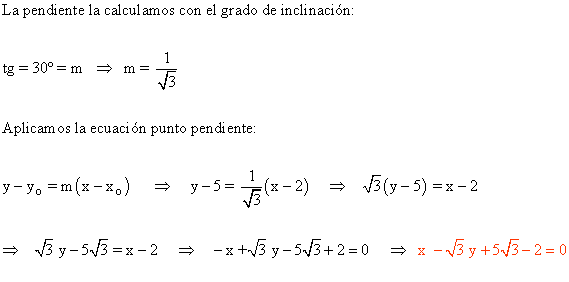
19-a ) Halla un vector normal y otro director de la recta r: x - 2y + 3 = 0
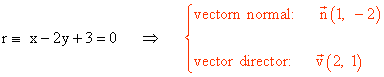
El producto escalar del vector normal y el vector director es 0:
![]()
19-b ) Hallar la ecuación general de la recta que contiene al punto (7, 3) y es paralela a la recta que tiene por ecuación 3x + y + 1 = 0 .
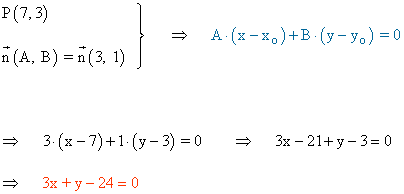
20-a ) Dada la ecuación de la recta r : 5x - 7y - 11 = 0 hallar los valores de p y ω y reducirla a su forma normal.
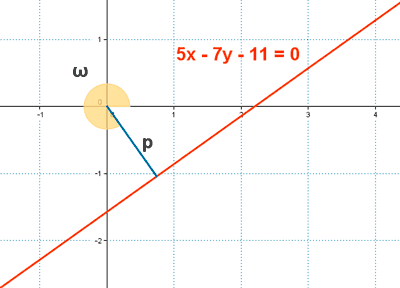
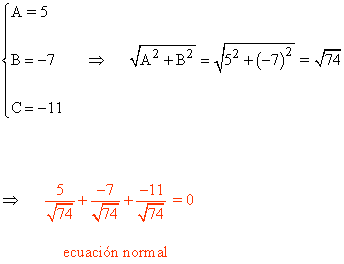
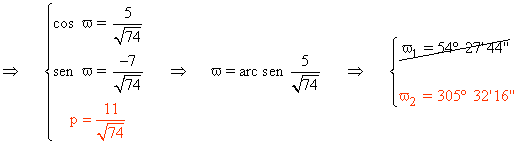
Elegimos ω2 ya que como se observa en el grafico, pertenece al cuarto cuadrante.
20-b ) Hallar los cosenos directores de la recta r : 3x + 4y - 8 = 0
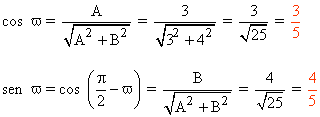
Por lo tanto, la ecuación normal es:
![]()
Resumen de tipos de ecuaciones de rectas
| Ecuaciones | Ejemplo |
|---|---|
Ecuación vectorial:
|
Hallar la ecuación de la recta determinada por el punto P(3, 1) y el vector v(1, -2):
|
Ecuación paramétrica:
|
|
Ecuación continua:
|
|
Ecuación general:
|
|
Ecuación explícita:
|
|
Ecuación punto pendiente:
|
Hallar la ecuación de la recta determinada por el punto P(1, -3) y de pendiente: -2:
|
Ecuación de la recta que pasa por dos puntos:
|
Hallar la ecuación de la recta que pasa por A(3, 2) y B(1, -1):
|
Ecuación canónica o segmentaria:
|
Escribe la ecuación canónica o segmentaria de la recta 3x + 5y = 15
|
Ecuación de la recta definida por un punto y un vector normal:
|
Hallar la ecuación de la recta que pasa por el punto P(3, 1) y tiene por vector normal n(2, 1):
|
Ecuación normal:
|
Halla la ecuación normal de la recta
|
Ecuación normal:
|
|


 INICIO
INICIO