Ecuaciones vectorial, paramétrica, continua y general de la recta
Elementos característicos de una recta
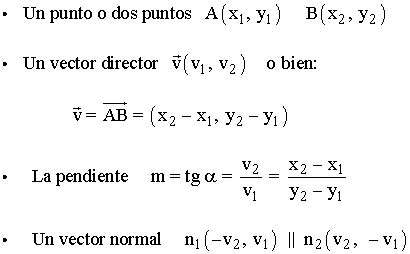
Ecuación vectorial
La ecuación vectorial de una recta r que pasa por un punto fijo P0(x0, y0) y que tiene como vector director v(v1, v2) se expresa de la siguiente manera:
![]()
Expresado en coordenadas viene dada por:
![]()
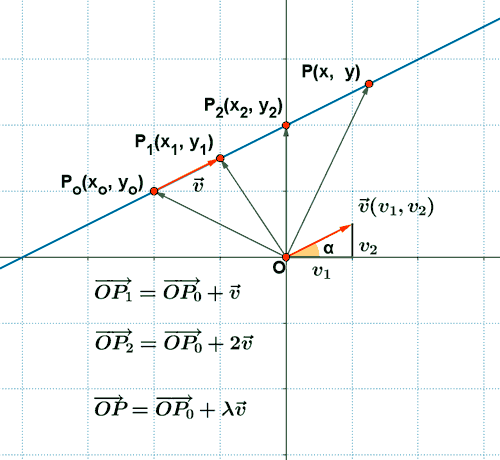
Ecuación paramétrica
La ecuación paramétrica de una recta r que pasa por un punto fijo P0(x0, y0) y que tiene como vector director v(v1, v2) viene dada por:
![]()
Igualando las componentes obtenemos que:
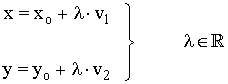
Ecuación continua
La ecuación continua se obtiene a partir de las ecuaciones paramétricas despejando λ en ambas ecuaciones:
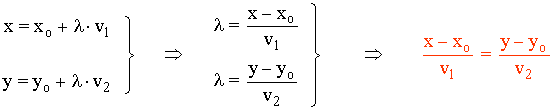
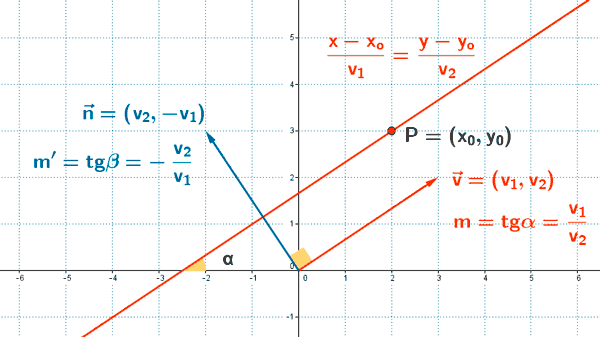
Ecuación general o implícita
La ecuación general se obtiene a partir de la ecuación continua:
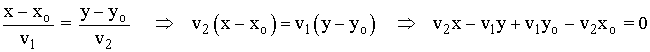
Tomando las siguientes igualdades:
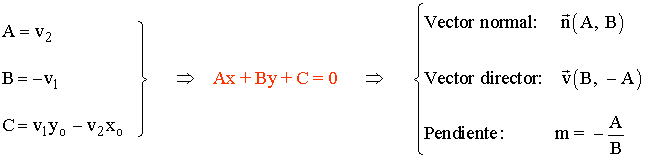
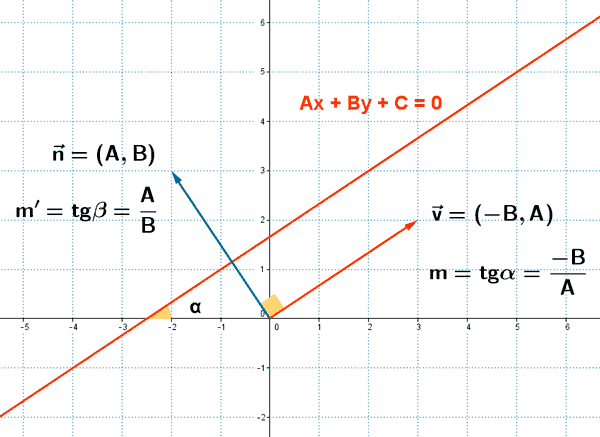
Ejemplos
1) Halla la ecuación vectorial, paramétrica, continua y general que pasa por el punto A(3, 1) y tiene como vector director v(1, -2).
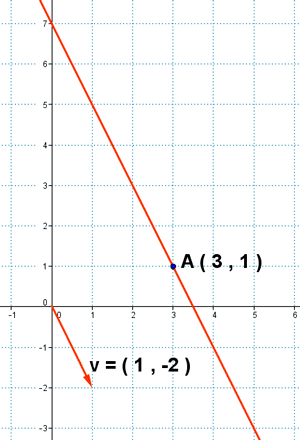
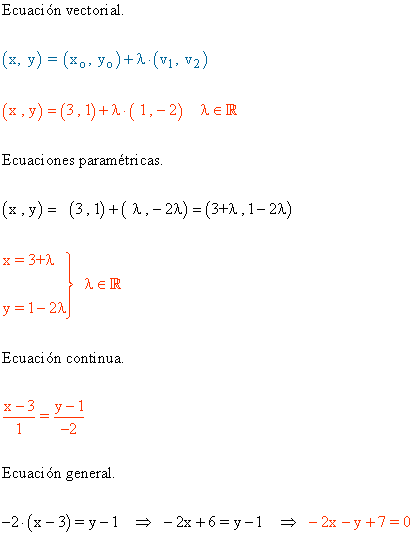
2) Encuentra la ecuación vectorial, paramétrica, continua y general que pasa por los puntos A(3 , 2) y B(1 , -1).
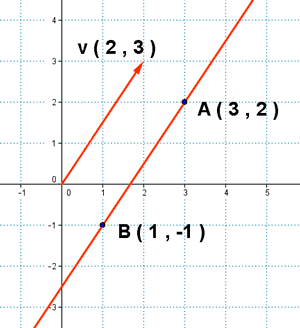



 INICIO
INICIO

