Problemas resueltos con incógnitas
1 ) Determina el valor de k para que los puntos A ( 2 , -1 ), B ( 1 , 4 ) y C ( k , 9 ) estén alineados.
2 ) Halla el valor de a para que las rectas r : 3x - 2y - 6 = 0 y s : ax + 6y - 1 = 0 no se corten.
3 ) considerando los puntos A ( -2 , 6 ), B ( 1 , 3 ) y C ( x , y ), calcular los valores de x e y para que C sea:
a ) El punto medio del segmento de extremos A y B.
b ) El simétrico de A con respecto a B.
4 ) Calcula el valor de a y b para que las rectas ax - y + 2 = 0 y bx + 6y -9 = 0 sean perpendiculares y además la segunda pase por el punto P = ( 1 , 1 ).
5 ) Calcula el valor de m para que las rectas r : kx + 2y + 6 = 0 s : 2x + y - 1 = 0 y t : x - y = 5 pasen, las tres, por un mismo punto.
6 ) Determina a y b sabiendo que la recta 2x + by = 0 pasa por el punto ( 1 , -2 ) y es paralela a la recta ax - 2y + 3 = 0.
7 ) ¿ Para que valores de m son perpendiculares las siguientes rectas ?
r : y = mx + 3
s : x - 2y + 6 = 0
8 ) Dadas las rectas:
r : 2x - y + 1 = 0
s : ax + 2y + 3 = 0
Hallar el valor de a para que:
a ) Las rectas sean paralelas.
b ) Las rectas sean perpendiculares.
c ) Las rectas sean secantes, pero no perpendicualres.
d ) La segunda recta pase por el punto P ( 3 , 4 ).
9 ) Dadas las rectas r : 3x + y = 3 y s : -2x + by = 8. Calcualas a para que el ángulos que forman entre ellas sea de 45º
10 ) Hallar b para que la distancia de O ( 0 , 0 ) a la recta r : 2x + by - 4 = 0 sea 2
11 ) Calcula el valor de a y b para que las rectas ax - 3y + 5 = 0 y bx + 2y -1=0 sean perpendiculares y además la segunda pase por el punto ( - 1 , 2 ).
12 ) ¿ Qué relación habrá entre a y b para que las rectas r : ax + y = 2 y s : bx + 2y = 10 sean paralelas? ¿ Y para que sean perpendiculares ?
13 ) Hallar el valor de K para que la distancia del punto P ( 2 , k ) a la recta r : 2x - 2y + 3 = 0 sea 2.
14 ) Hallar el valor de A para que las rectas 2x + y - 2 = 0 y Ax + y + 1 = 0, formen un ángulo de π/3 radianes.
15 ) Halla el valor de a para que las rectas r : 2x + ay + 12 = 0 s : 6x - 2y = 10
a ) Sean paralelas. Una vez vistas que son paralelas calcular su distancia.
b ) Sean perpendicualres.
16 ) Dadas las rectas r : x - 2y = 2 y s : 2x - y + 6 = 0 , hallar todas las rectas que pasen por el punto P ( 2 , 2 ) y que formen con r y s ángulos iguales.
17 ) Calcula el valor de k para que la recta x + y = k forme con los ejes coordenados un triángulo de 12.5 unidades cuadradas de área.
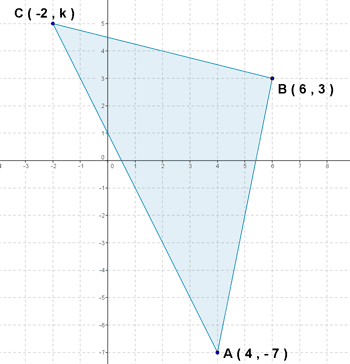
18 ) Calcula el valor de k para que el triángulo de vértices A ( 4 , -7 ), B ( 6 , 3 ) y C ( -2 , k ) tengan por área 42 unidades cuadradas.
19 ) Dados los puntos A(5, 4) , B((7, 3) y C(3, -1) halla el punto D de modo que ABCD sea un paralelogramo. Hallar los ángulos del paralelogramo.
20 ) Dados los puntos A(2, 1) y B(4, 3) determinar un punto C para que el triángulo ABC sea isósceles y su área sea 4.
1 ) Determina el valor de k para que los puntos A ( 2 , -1 ), B ( 1 , 4 ) y C ( k , 9 ) estén alineados.
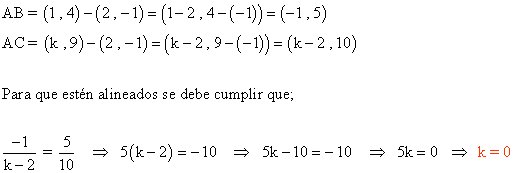
Podriamos resolverlo de otra manera:

2 ) Halla el valor de a para que las rectas r : 3x - 2y - 6 = 0 y s : ax + 6y - 1 = 0 no se corten.
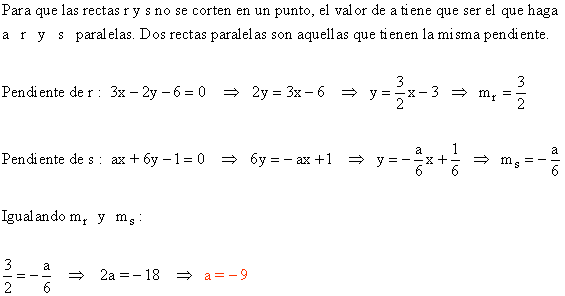
3 ) considerando los puntos A ( -2 , 6 ), B ( 1 , 3 ) y C ( x , y ), calcular los valores de x e y para que C sea:
a ) El punto medio del segmento de extremos A y B.
b ) El simétrico de A con respecto a B.
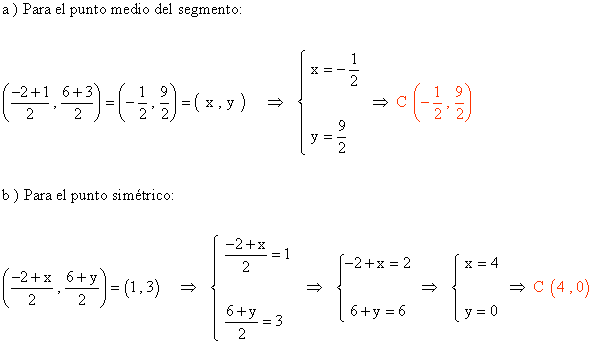
4 ) Calcula el valor de a y b para que las rectas ax - y + 2 = 0 y bx + 6y -9 = 0 sean perpendiculares y además la segunda pase por el punto P = ( 1 , 1 ).

5 ) Calcula el valor de m para que las rectas r : kx + 2y + 6 = 0 s : 2x + y - 1 = 0 y t : x - y = 5 pasen, las tres, por un mismo punto.
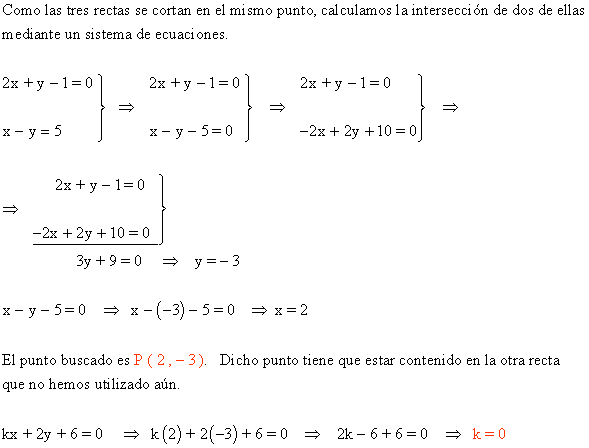
6 ) Determina a y b sabiendo que la recta 2x + by = 0 pasa por el punto ( 1 , -2 ) y es paralela a la recta ax - 2y + 3 = 0.

7 ) ¿ Para que valores de m son perpendiculares las siguientes rectas ?
r : y = mx + 3
s : x - 2y + 6 = 0

8 ) Dadas las rectas:
r : 2x - y + 1 = 0
s : ax + 2y + 3 = 0
Hallar el valor de a para que:
a ) Las rectas sean paralelas.
b ) Las rectas sean perpendiculares.
c ) Las rectas sean secantes, pero no perpendicualres.
d ) La segunda recta pase por el punto P ( 3 , 4 ).

9 ) Dadas las rectas r : 3x + y = 3 y s : -2x + by = 8. Calcualas a para que el ángulos que forman entre ellas sea de 45º
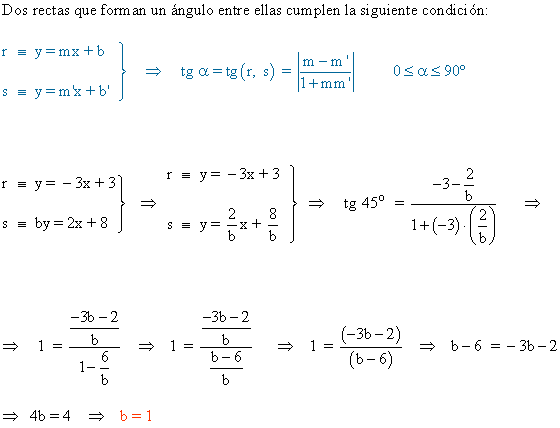
10 ) Hallar b para que la distancia de O ( 0 , 0 ) a la recta r : 2x + by - 4 = 0 sea 2
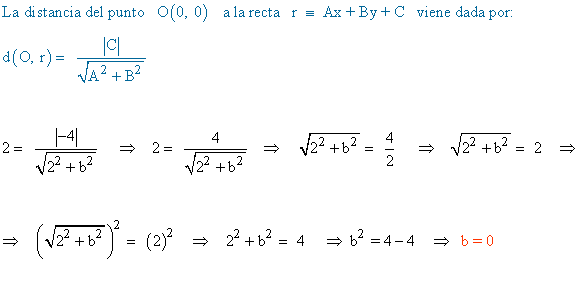
11 ) Calcula el valor de a y b para que las rectas ax - 3y + 5 = 0 y bx + 2y -1=0 sean perpendiculares y además la segunda pase por el punto ( - 1 , 2 )

12 ) ¿ Qué relación habrá entre a y b para que las rectas r : ax + y = 2 y s : bx + 2y = 10 sean paralelas? ¿ Y para que sean perpendiculares ?
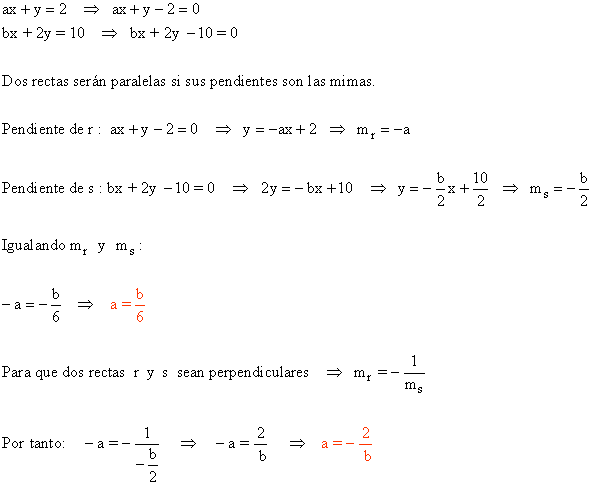
13 ) Hallar el valor de K para que la distancia del punto P ( 2 , k ) a la recta r : 2x - 2y + 3 = 0 sea 2.
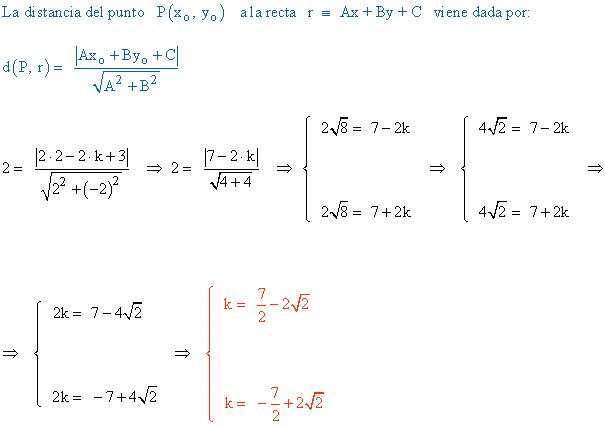
14 ) Hallar el valor de A para que las rectas 2x + y - 2 = 0 y Ax + y + 1 = 0, formen un ángulo de π/3 radianes.
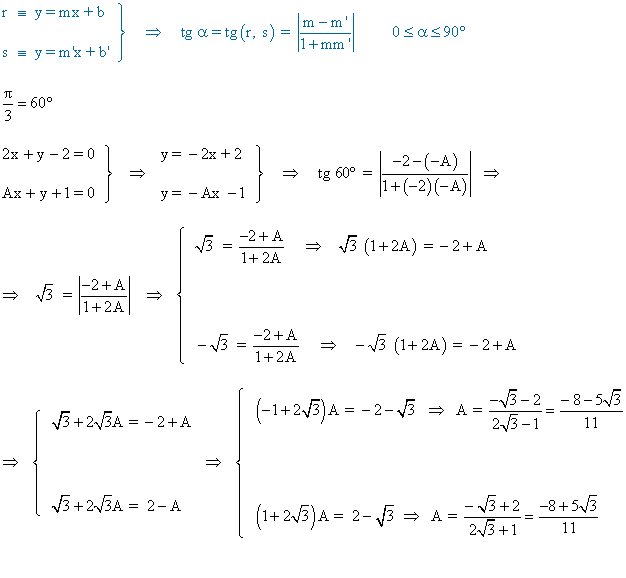
15 ) Halla el valor de a para que las rectas r : 2x + ay + 12 = 0 s : 6x - 2y = 10
a ) Sean paralelas. Una vez vistas que son paralelas calcular su distancia.
b ) Sean perpendicualres.
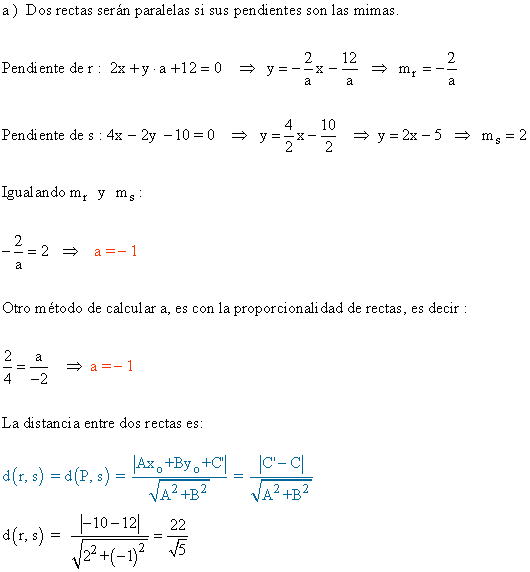
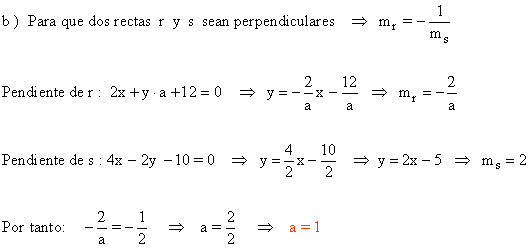
16 ) Dadas las rectas r : x - 2y = 2 y s : 2x - y + 6 = 0 , hallar todas las rectas que pasen por el punto P ( 2 , 2 ) y que formen con r y s ángulos iguales.
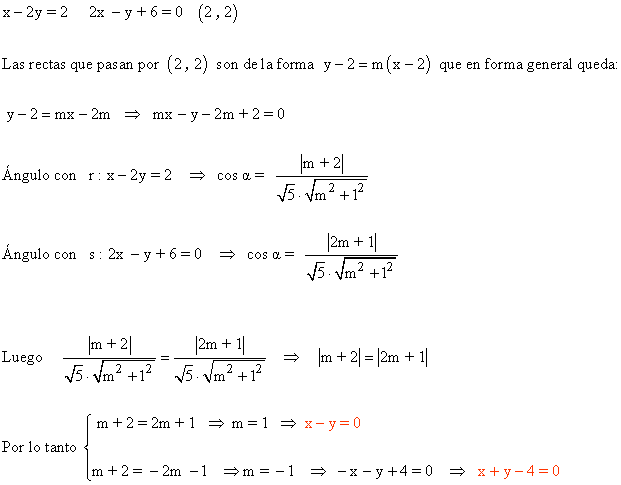
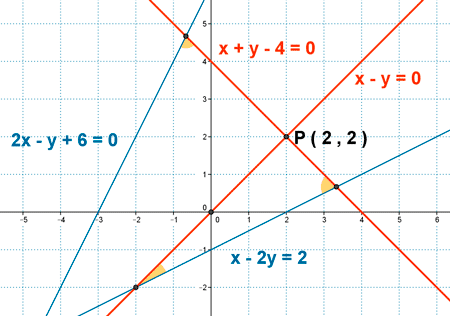
17 ) Calcula el valor de k para que la recta x + y = k forme con los ejes coordenados un triángulo de 12.5 unidades cuadradas de área.
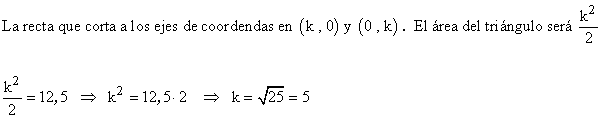
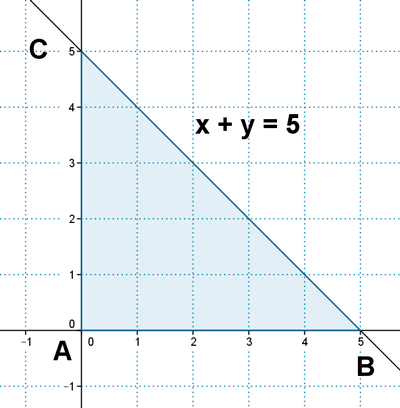
18 ) Calcula el valor de k para que el triángulo de vértices A ( 4 , -7 ), B ( 6 , 3 ) y C ( -2 , k ) tengan por área 42 unidades cuadradas.
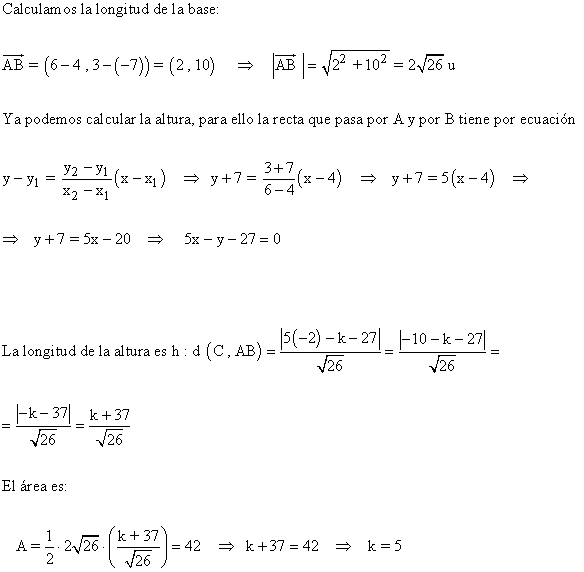
19 ) Dados los puntos A(5, 4) , B((7, 3) y C(3, -1) halla el punto D de modo que ABCD sea un paralelogramo. Hallar los ángulos del paralelogramo.
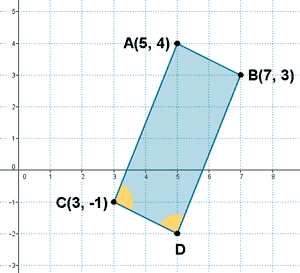
Para que ABCD sea un paralelogramo tiene que darse que:
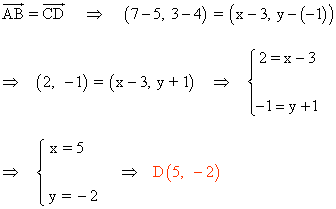
Para calcular los ángulos del paralelogramo utilizamos la siguiente fórmula:
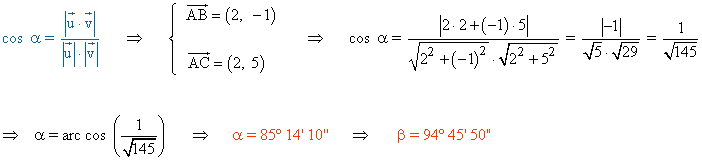
20 ) Dados los puntos A(2, 1) y B(4, 3) determinar un punto C para que el triángulo ABC sea isósceles y su área sea 4.
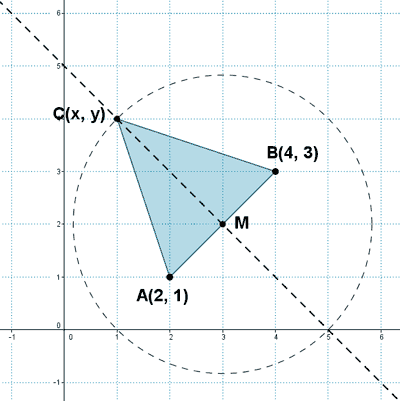
Para que el triángulo sea isósceles, la longitud de los segmentos AC y BD tienen que ser iguales:
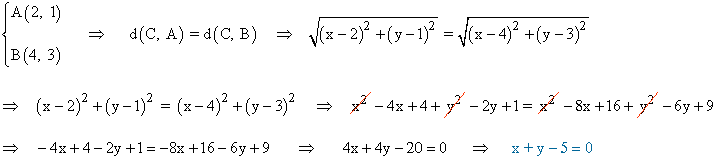
Como el área del triángulo tiene que ser 5:
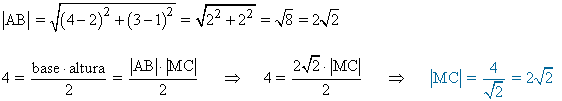
Por lo tanto tenemos dos condiciones para el punto C :
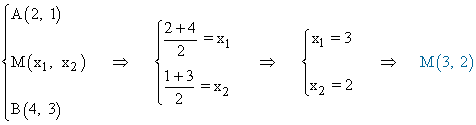
Conociendo el punto M hallamos la condición para la altura del segmento MC :
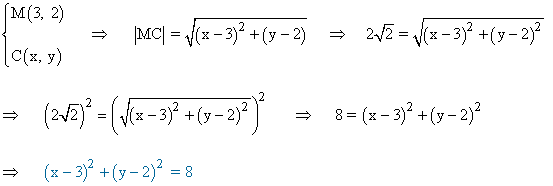
De esta forma, el pnto C queda determinado por la intersección de las siguientes ecuaciones:
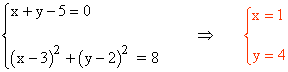


 INICIO
INICIO