Posiciones relativas de puntos, rectas y circunferencias
Posiciones relativas de un punto y una circunferencia
Un punto puede ser perteneciente, exterior o interior a una circunferencia
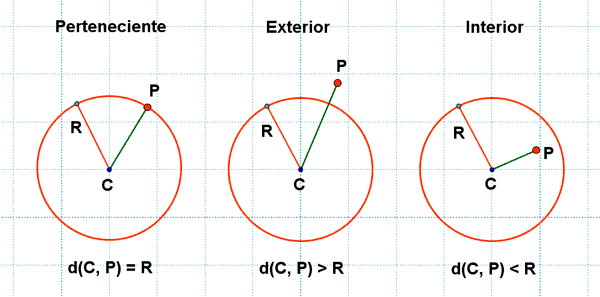
Ejemplo:
Dada la circunferencia x2 + y2 - 8y = 0 halla la posición relativa respecto a los siguientes puntos A(-2 , 1) , B(0 , 8) , D(1 , -2).
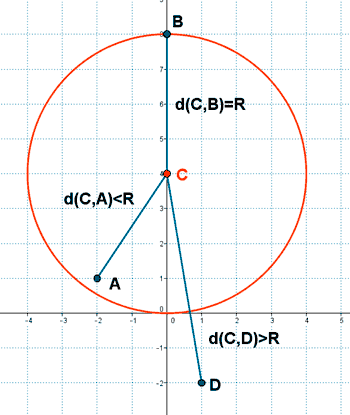
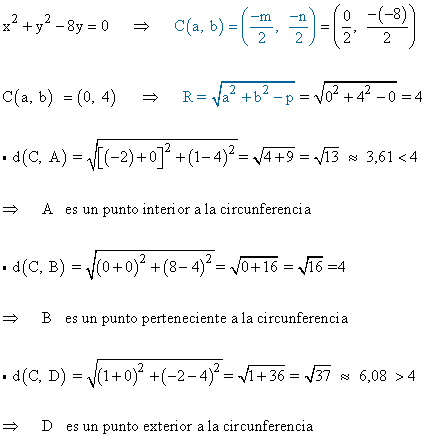
Posiciones relativas de una recta y una circunferencia
Una recta puede ser secante, tangente o exterior a una circunferencia
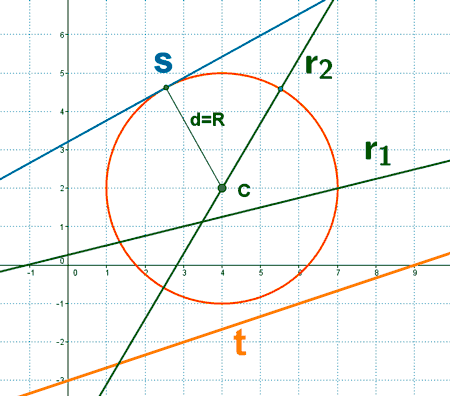
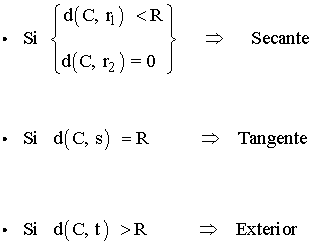
Ejemplo:
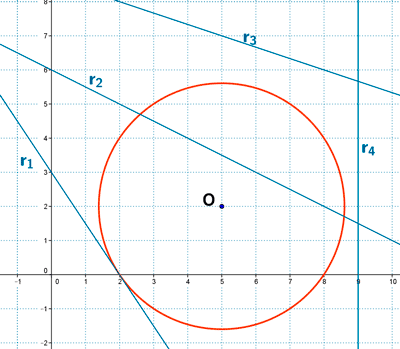
Dada la siguiente circunferencia:
x² + y² - 10x - 4y + 16 = 0
Hallar la posición relativa de las siguientes rectas respecto a dicha circunferencia :
a ) r1: 3x + 2y - 6 = 0
b ) r2: x + 2y - 12 = 0
c ) r3: x + 3y - 26 = 0
d ) r4: x - 9 = 0

Posiciones relativas de dos circunferencias
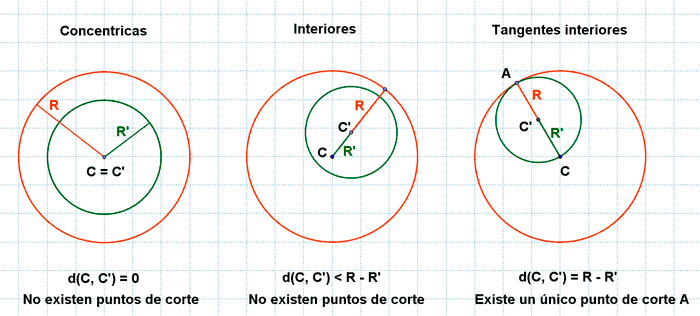
Posición relativa de dos circunferencias interiores:
Dos circunferencias interiores pueden ser concentricas, interiores o tangentes interiores.
Ejemplo:
Halla los puntos de intersección de las siguientes circunferencias y calcula su posición relativa:
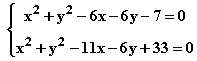
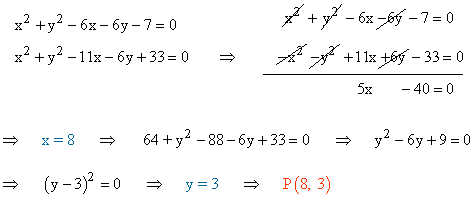
Aplicamos la fórmula para calcular los centros y radios de ambas circunferencias:
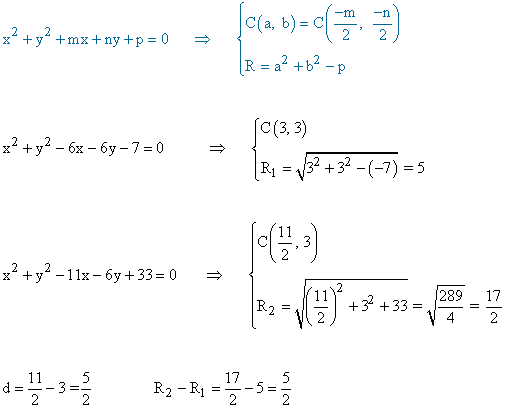
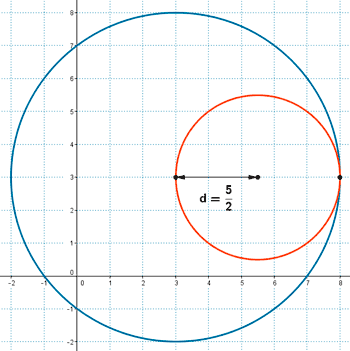
Como la distancia entre sus centros es d =5/2 coincide con la diferencia de sus radios, es decir, d = R2 - R1 entonces ambas circunferencias son tangentes interiores.
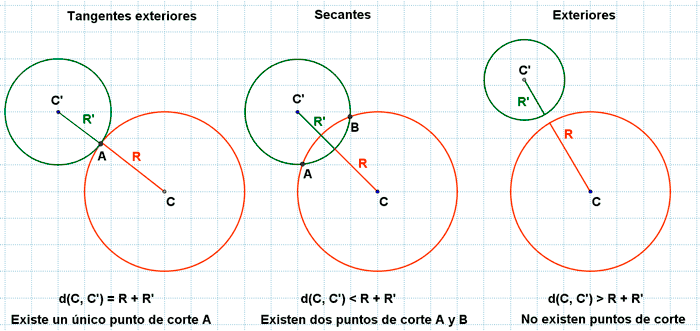
Posición relativa de dos circunferencias exteriores:
Dos circunferencias exteriores pueden ser tangentes exteriores, secantes o exteriores.
Ejemplo:
Halla los puntos de intersección de las siguientes circunferencias y calcula su posición relativa:
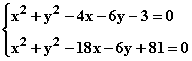
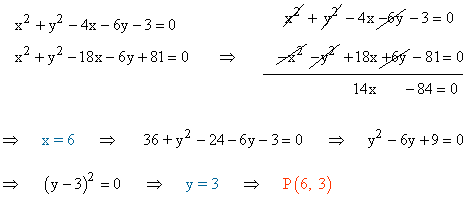
Aplicamos la fórmula para calcular los centros y radios de ambas circunferencias:
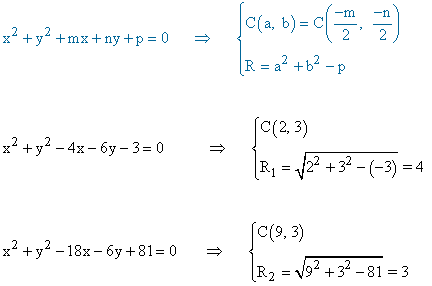
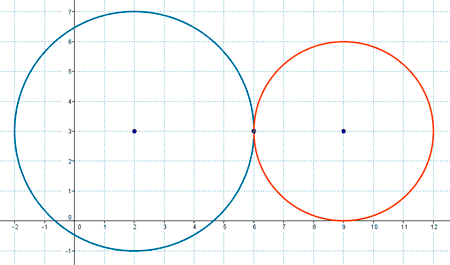
Como la distancia entre sus centros es d = 7 que coincide con la suma de sus radios, es decir, d = R1 + R2 entonces ambas circunferencias son tangentes exteriores.


 INICIO
INICIO

