Estimación de resultados
Las rectas de regresión nos permiten obtener los valores de una variable conociendo los valores de la otra. Estos valores se llaman estimaciones de la variable.
- Las estimaciones realizadas a través de la recta de regresión serán fiables siempre que el coeficiente de correlación lineal r tome valores próximos a 1 ó -1.
- En los casos en que el coeficiente de correlación lineal esté próximo a 0, las estimaciones carecerán de validez.
- Las estimaciones tienen validez para los valores de la variable próximos a los datos.
Ejemplo 1:
Se ha medido el contenido en oxígeno Y, en mg/litro, de un lago a una profundidad de X metros, obteniéndose los siguientes datos:
| X | 15 | 20 | 30 | 40 | 50 | 60 | 70 |
|---|---|---|---|---|---|---|---|
| Y | 6,5 | 5,6 | 5,4 | 6 | 4,6 | 1,4 | 0,1 |
La recta de regresión es Y - 4,22 = (- 38,59/360,5)·[X - 40,71]
Calcular:
a) Coeficiente de correlación, conclusión estadística.
b) Para una profundidad comprendida entre 75 y 80 metros, ¿qué contenido en oxígeno se podría predecir?
a)
| 15 | 6,5 | 225 | 42,25 | 97,5 | |
| 20 | 5,6 | 400 | 31,36 | 112 | |
| 30 | 5,4 | 900 | 29,16 | 162 | |
| 40 | 6 | 1600 | 36 | 240 | |
| 50 | 4,6 | 2500 | 21,16 | 230 | |
| 60 | 1,4 | 3600 | 1,96 | 84 | |
| 70 | 0,1 | 4900 | 0,01 | 7 | |
| Total | 285 | 29.6 | 14125 | 161,9 | 932,5 |
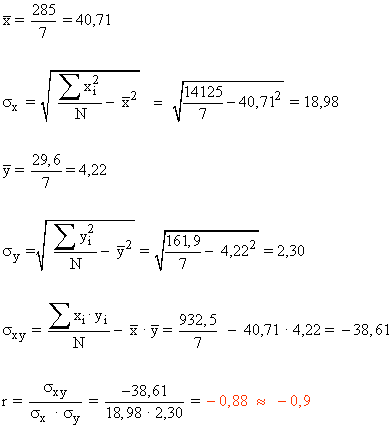
Como el coeficiente de correlación lineal es próximo a -1, hay un alto grado de correlación entre ambas variables aunque negativa o inversa, es decir, a medida que aumentamos la profundidad, disminuye el contenido de oxígeno.
b)
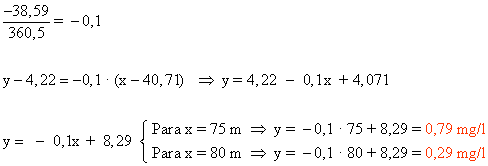


 INICIO
INICIO

