Correlación lineal
El coeficiente de correlación lineal o coeficiente de Pearson, r , es una medida de la variable(X, Y) que determina el grado de dependencia lineal entre las variables X e Y.
Utilizando la fórmula:
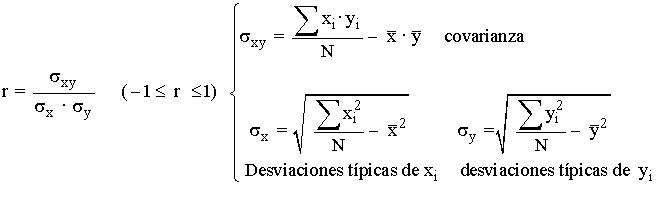
-Donde σxy es la covarianza o varianza conjunta de las variables X e Y.
-σx y σy son las desviaciones típicas de las variables marginales X e Y.
Escala de valores del coeficiente de correlación lineal
- Si -1 < r < 0 existe correlación lineal negativa o inversa y será más fuerte cuanto más se aproxime r a -1.
- si 0 < r < 1 existe correlación lineal positiva o directa y será más fuerte cuanto más se aproxime r a 1.
- Si r = 1 ó r = -1, la correlación es una dependencia lineal directa (+1) ó inversa (-1).
- Si r = 0 independencia, no existe correlación lineal, aunque pueden estar relacionadas por una correlación curvilínea.
Ejemplo 1:
En una empresa se seleccionan 5 trabajadores, se anotaron sus años de servicio y el tiempo de permiso en horas, solicitado el último mes. Los resultados obtenidos fueron:
| X | 1 | 3 | 2 | 4 | 5 | 4 |
|---|---|---|---|---|---|---|
| Y | 1 | 1 | 3 | 4 | 6 | 5 |
a) Representar gráficamente los datos anteriores. Razonar si los datos muestran correlación positiva o negativa.
b) Calcular el coeficiente de correlación e interpertarlo en términos de la situación real.
a)
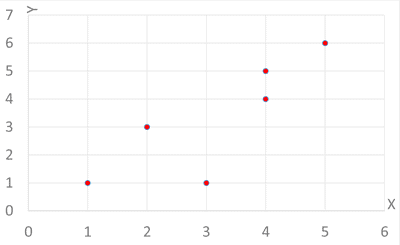
Los datos muestran una correlación directa o positiva, pues cuando crece x también crece y.
b)
| 1 | 1 | 1 | 1 | 1 | |
| 3 | 1 | 9 | 1 | 3 | |
| 2 | 3 | 4 | 9 | 6 | |
| 4 | 4 | 16 | 16 | 16 | |
| 5 | 6 | 25 | 36 | 30 | |
| 4 | 5 | 16 | 25 | 20 | |
| Total | 19 | 20 | 71 | 88 | 76 |
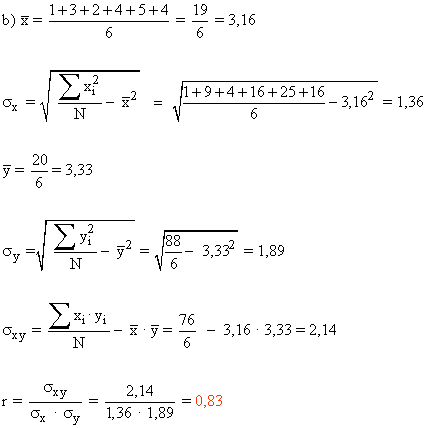
Interpretación: como el coeficiente de correlación es 0,82 (que varía entre -1 y 1) podemos deducir que existe bastante relación entre una variable y otra. Y además se trata de una relación creciente, en el sentido de que al aumentar los valores de la X (número de horas de servicio) aumentan los valores de la Y (las horas de permiso).
Ejemplo 2:
En la siguiente tabla se dan las marcas femeninas de cierta reunión de atletismo:
| Distancia (m) | 100 | 200 | 400 | 800 | 1500 |
|---|---|---|---|---|---|
| Tiempo : Minutos | 0 | 0 | 0 | 1 | 3 |
| Tiempo : Segundos | 11 | 22 | 48 | 54 | 53 |
a) Calcular el coeficiente de correlación entre las distancias (m) y los tiempos medidos en segundos.
b) Sin efectuar cálculos, razonar si debemos esperar correlación positiva o negativa entre las variables velocidad y distancia.
a)
| 100 | 11 | 10000 | 121 | 1100 | |
| 200 | 22 | 40000 | 484 | 4400 | |
| 400 | 48 | 160000 | 2304 | 19200 | |
| 800 | 114 | 640000 | 12996 | 91200 | |
| 1500 | 233 | 2250000 | 54289 | 349500 | |
| Total | 3000 | 428 | 3100000 | 70194 | 465400 |
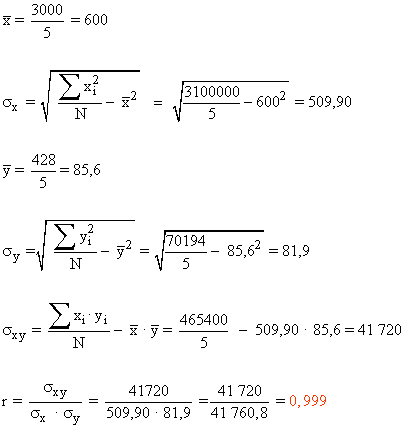


 INICIO
INICIO

