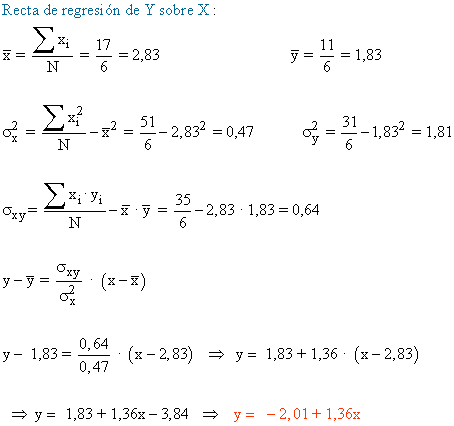Problemas resueltos de recta de regresión y correlación lineal.
1) En las gráficas siguientes se muestran las rectas de regresión en tres estudios de regresión lineal.
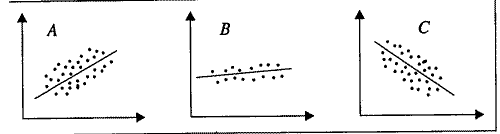
a) ¿En cuál de las dos gráficas, ( A ó B ), el coeficiente de correlación lineal sería más grande?
b) Indicar en qué gráficas el coeficiente de correlación lineal sería negativo. Justificar la respuesta.2) En una empresa de transporte trabajan 4 conductores. Los años de antigüedad de sus permisos de conducir y el número de infracciones cometidas en el último año por cada uno de ellos son los siguientes :
X : años de antigüedad
3
4
5
6
Y : infracciones
4
3
2
1
| X : años de antigüedad | 3 | 4 | 5 | 6 |
|---|---|---|---|---|
| Y : infracciones | 4 | 3 | 2 | 1 |
a) Representar gráficamente los datos anteriores. Razonar si los datos muestran una correlación positiva o negativa.
b) Calcular el coeficiente de correlación e interpretarlo en términos de la situación real.3) Una persona rellena semanalmente una quiniela y un boleto de lotería primitiva, anotando el número de aciertos que tiene. Durante las 4 semanas del mes de febrero, los aciertos fueron :
Semana
1ª
2ª
3ª
4ª
Aciertos en la quiniela
6
8
6
8
Aciertos en la primitiva
1
2
2
1
| Semana | 1ª | 2ª | 3ª | 4ª |
|---|---|---|---|---|
| Aciertos en la quiniela | 6 | 8 | 6 | 8 |
| Aciertos en la primitiva | 1 | 2 | 2 | 1 |
Obtener el coeficiente de correlación lineal e interpretarlo. ¿Ofrecerían confianza las predicciónes hechas con las rectas de regresión?
4) En una empresa trabajan cuatro obreros. La antigüedad y el número de productos defectuosos elaborados por ellos durante el último año viene dado por :
Antigüedad
3
2
4
1
Productos defectuosos
4
3
3
4
| Antigüedad | 3 | 2 | 4 | 1 |
|---|---|---|---|---|
| Productos defectuosos | 4 | 3 | 3 | 4 |
a) Representar gráficamente los datos. Razonar si los datos expresan correlación positiva o negativa.
b) Calcular el coeficiente de correlación.
5) Representa gráficamente la distribución bidimensional correspondiente a la siguiente tabla :
Variable X
2
4
6
8
Variable Y
2
5
7
10
| Variable X | 2 | 4 | 6 | 8 |
|---|---|---|---|---|
| Variable Y | 2 | 5 | 7 | 10 |
a) A la vista de la gráfica, ¿qué valor aproximado tendrá el coeficiente de correlación lineal?
b) Calcula dicho coeficiente indicando todos los paso seguidos para ello.
6) En cinco estudios estadísticos se han obtenido los siguientes coeficientes de correlación lineal :
r = -0,98 ; r = 0,93 ; r = 0,05 ; r = 0,71 ; r = -0,62
Identificar ( justificando la respuesta ) la nube de puntos correspondiente a cada uno de ellos.
7) En una empresa se seleccionan 5 trabajadores, se anotaron sus años de servicio y el tiempo de permiso en horas, solicitado el último mes. Los resultados obtenidos fueron:
| X | 1 | 3 | 2 | 4 | 5 | 4 |
|---|---|---|---|---|---|---|
| Y | 1 | 1 | 3 | 4 | 6 | 5 |
a) Representar gráficamente los datos anteriores. Razonar si los datos muestran correlación positiva o negativa.
b) Calcular el coeficiente de correlación e interpertarlo en términos de la situación real.
8) En la siguiente tabla se dan las marcas femeninas de cierta reunión de atletismo:
| Distancia (m) | 100 | 200 | 400 | 800 | 1500 |
|---|---|---|---|---|---|
| Tiempo : Minutos | 0 | 0 | 0 | 1 | 3 |
| Tiempo : Segundos | 11 | 22 | 48 | 54 | 53 |
a) Calcular el coeficiente de correlación entre las distancias (m) y los tiempos medidos en segundos.
b) Sin efectuar cálculos, razonar si debemos esperar correlación positiva o negativa entre las variables velocidad y distancia.
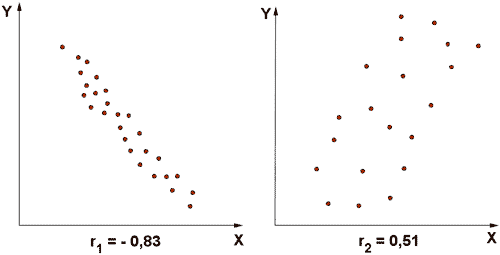
9) Dos conjuntos de datos bidimensionales tienen como coeficiente de correlación r1 = - 0,83 y r2 = 0,51.
a) Representar gráficamente dos conjuntos de puntos cuyas correlaciones reflejen aproximadamente las dadas.
b) Razonar cuál de los dos conjuntos estará más concentrado respecto a sus correspondientes rectas de regresión.
10) Las puntuaciones en Matemáticas y Física de siete alumnos han sido las siguientes :
Matemáticas
8
8
6
7
8
6
2
Física
7
7,5
5
7
7,5
5
7
| Matemáticas | 8 | 8 | 6 | 7 | 8 | 6 | 2 |
|---|---|---|---|---|---|---|---|
| Física | 7 | 7,5 | 5 | 7 | 7,5 | 5 | 7 |
a) Halla el coeficiente de correlación de las calificaciones en Matemáticas y Física de los seis primeros alumnos.
b) Calcula el coeficiente de correlación de esas dos variables para los siete alumnos.
c) Explica la direfencia entre los resultados obtenidos.
11) La siguiente tabla ofrece los resultados de seis pares de observaciones, realizadas para analizar el grado de relación existente entre dos variables X e Y:
| X | 2 | 2 | 3 | 3 | 3 | 4 |
|---|---|---|---|---|---|---|
| Y | 0 | 1 | 1 | 2 | 4 | 3 |
Obtener:
a) Recta de regresión de Y sobre X.
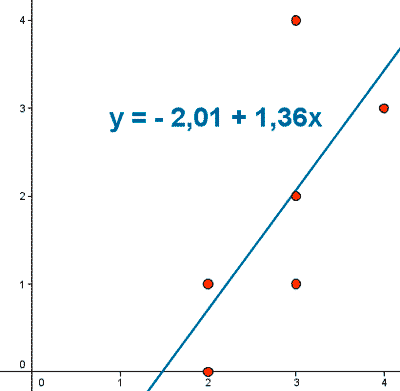
b) Representación gráfica de la misma, así como de los pares de observaciones anteriores.
c) ¿Qué grado de relación lineal existe entre ambas variables?
1) En las gráficas siguientes se muestran las rectas de regresión en tres estudios de regresión lineal.

a) ¿En cuál de las dos gráficas, ( A ó B ), el coeficiente de correlación lineal sería más grande?
b) Indicar en qué gráficas el coeficiente de correlación lineal sería negativo. Justificar la respuesta.
a)
En la gráfica A, los puntos de la nube de puntos se encuentran más dispersos y alejados de la recta de regresión. Sin embargo, en la gráfica B dichos puntos están más próximos y concentrados alrededor de la recta de regresión. Por tanto, el gráfico B tiene un mayor coeficiente de correlación lineal.
b)
En la gráfica C la correlación es negativa, ya que a mayores valores de X disminuye el valor de Y. Es en esta gráfica donde el coeficiente de correlación lineal es negativo.
2) En una empresa de transporte trabajan 4 conductores. Los años de antigüedad de sus permisos de conducir y el número de infracciones cometidas en el último año por cada uno de ellos son los siguientes :
X : años de antigüedad
3
4
5
6
Y : infracciones
4
3
2
1
| X : años de antigüedad | 3 | 4 | 5 | 6 |
|---|---|---|---|---|
| Y : infracciones | 4 | 3 | 2 | 1 |
a) Representar gráficamente los datos anteriores. Razonar si los datos muestran una correlación positiva o negativa.
b) Calcular el coeficiente de correlación e interpretarlo en términos de la situación real.
a)
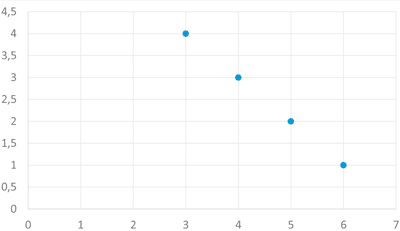
Al aumentar los valores de X los valores de Y disminuye, por lo que la correlación de ambas variables es negativa.
| xi | yi | xi2 | yi2 | xi · yi |
|---|---|---|---|---|
| 3 | 4 | 9 | 16 | 12 |
| 4 | 3 | 16 | 9 | 12 |
| 5 | 2 | 25 | 4 | 10 |
| 6 | 1 | 36 | 1 | 6 |
| 18 | 10 | 86 | 30 | 40 |
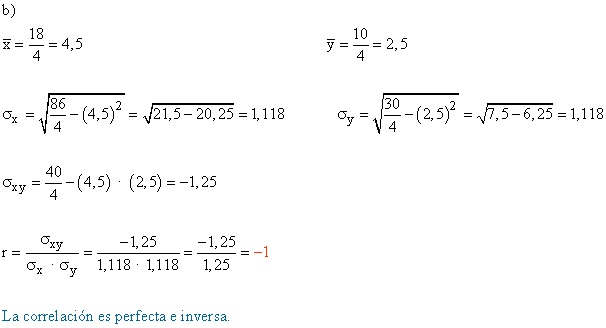
3) Una persona rellena semanalmente una quiniela y un boleto de lotería primitiva, anotando el número de aciertos que tiene. Durante las 4 semanas del mes de febrero, los aciertos fueron :
Semana
1ª
2ª
3ª
4ª
Aciertos en la quiniela
6
8
6
8
Aciertos en la primitiva
1
2
2
1
| Semana | 1ª | 2ª | 3ª | 4ª |
|---|---|---|---|---|
| Aciertos en la quiniela | 6 | 8 | 6 | 8 |
| Aciertos en la primitiva | 1 | 2 | 2 | 1 |
Obtener el coeficiente de correlación lineal e interpretarlo. ¿Ofrecerían confianza las predicciónes hechas con las rectas de regresión?
| xi | yi | xi2 | yi2 | xi · yi |
|---|---|---|---|---|
| 6 | 1 | 36 | 1 | 6 |
| 8 | 2 | 64 | 4 | 16 |
| 6 | 2 | 36 | 4 | 12 |
| 8 | 1 | 64 | 1 | 8 |
| 28 | 6 | 200 | 10 | 42 |
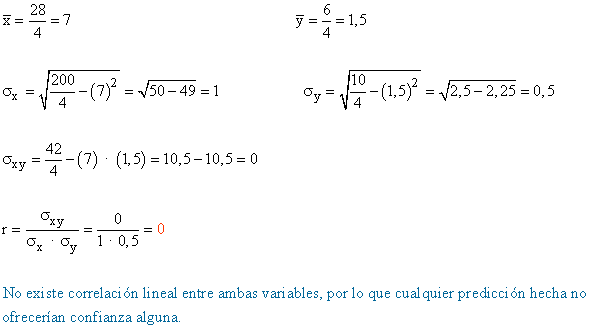
4) En una empresa trabajan cuatro obreros. La antigüedad y el número de productos defectuosos elaborados por ellos durante el último año viene dado por :
Antigüedad
3
2
4
1
Productos defectuosos
4
3
3
4
| Antigüedad | 3 | 2 | 4 | 1 |
|---|---|---|---|---|
| Productos defectuosos | 4 | 3 | 3 | 4 |
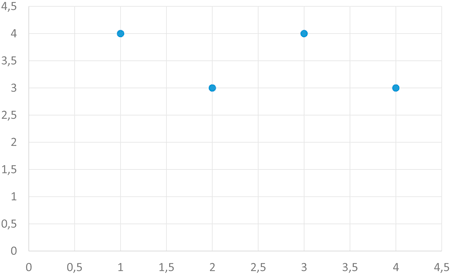
a) Representar gráficamente los datos. Razonar si los datos expresan correlación positiva o negativa.
b) Calcular el coeficiente de correlación.
a)
| xi | yi | xi2 | yi2 | xi · yi |
|---|---|---|---|---|
| 1 | 4 | 1 | 16 | 4 |
| 2 | 3 | 4 | 9 | 6 |
| 3 | 4 | 9 | 16 | 12 |
| 4 | 3 | 16 | 9 | 12 |
| 10 | 14 | 30 | 50 | 34 |

5) Representa gráficamente la distribución bidimensional correspondiente a la siguiente tabla :
Variable X
2
4
6
8
Variable Y
2
5
7
10
| Variable X | 2 | 4 | 6 | 8 |
|---|---|---|---|---|
| Variable Y | 2 | 5 | 7 | 10 |
a) A la vista de la gráfica, ¿qué valor aproximado tendrá el coeficiente de correlación lineal?
b) Calcula dicho coeficiente indicando todos los paso seguidos para ello.
a)
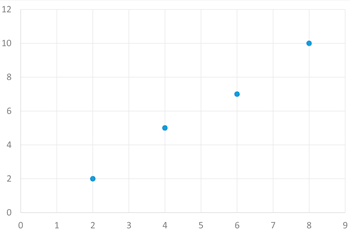
Los puntos de la nube se encuentran muy próximos a una recta, y al aumentar los valores de la variable X aumentan los valores de la variable Y. Basándonos en esto, podemos afirmar que la correlación lineal entre ambas variables es positiva y grande. El coeficiente de correlación lineal estaría próximo a 1.
b)
| xi | yi | xi2 | yi2 | xi · yi |
|---|---|---|---|---|
| 2 | 2 | 4 | 4 | 4 |
| 4 | 5 | 16 | 25 | 20 |
| 6 | 7 | 36 | 49 | 42 |
| 8 | 10 | 64 | 100 | 80 |
| 20 | 24 | 120 | 178 | 146 |
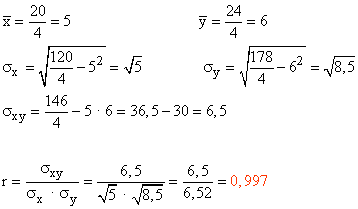
6) En cinco estudios estadísticos se han obtenido los siguientes coeficientes de correlación lineal :
r = -0,98 ; r = 0,93 ; r = 0,05 ; r = 0,71 ; r = -0,62
Identificar ( justificando la respuesta ) la nube de puntos correspondiente a cada uno de ellos.

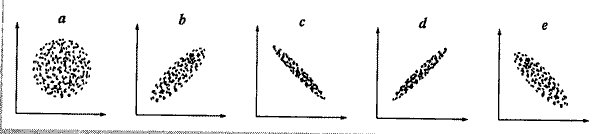
En la gráfica " a " la nube de puntos se encuentra completamente dispersa, por lo que podemos afirmar que la correlación es practicamente nula : r = 0,05 .
En " b " la correlación lineal es positiva, y dado que la nube de puntos no está del todo concentrada, la correlación es más bien moderada : r = 0,71 .
En la gráfica " c " la correlación lineal es fuerte y además negativa : r = -0,98 .
En " d " es positiva y además la correlación es fuerte : r = 0,93 .
Por último, en la gráfica " e ", la correlación es moderada y negativa : r = -0,62 .
7) En una empresa se seleccionan 5 trabajadores, se anotaron sus años de servicio y el tiempo de permiso en horas, solicitado el último mes. Los resultados obtenidos fueron:
| X | 1 | 3 | 2 | 4 | 5 | 4 |
|---|---|---|---|---|---|---|
| Y | 1 | 1 | 3 | 4 | 6 | 5 |
a) Representar gráficamente los datos anteriores. Razonar si los datos muestran correlación positiva o negativa.
b) Calcular el coeficiente de correlación e interpertarlo en términos de la situación real.
a)
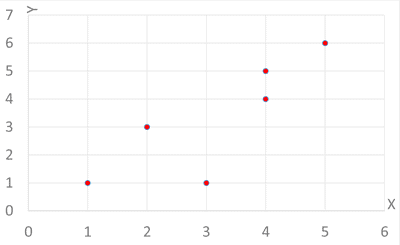
Los datos muestran una correlación directa o positiva, pues cuando crece x también crece y.
b)
| 1 | 1 | 1 | 1 | 1 | |
| 3 | 1 | 9 | 1 | 3 | |
| 2 | 3 | 4 | 9 | 6 | |
| 4 | 4 | 16 | 16 | 16 | |
| 5 | 6 | 25 | 36 | 30 | |
| 4 | 5 | 16 | 25 | 20 | |
| Total | 19 | 20 | 71 | 88 | 76 |
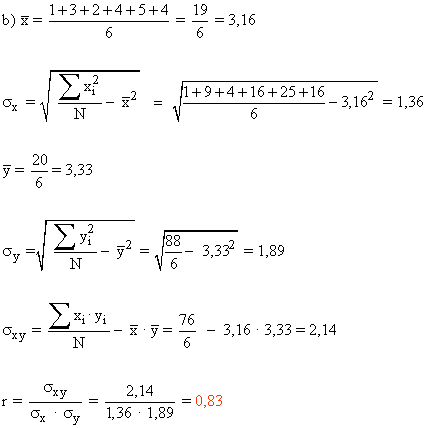
Interpretación: como el coeficiente de correlación es 0,82 (que varía entre -1 y 1) podemos deducir que existe bastante relación entre una variable y otra. Y además se trata de una relación creciente, en el sentido de que al aumentar los valores de la X (número de horas de servicio) aumentan los valores de la Y (las horas de permiso).
8) En la siguiente tabla se dan las marcas femeninas de cierta reunión de atletismo:
| Distancia (m) | 100 | 200 | 400 | 800 | 1500 |
|---|---|---|---|---|---|
| Tiempo : Minutos | 0 | 0 | 0 | 1 | 3 |
| Tiempo : Segundos | 11 | 22 | 48 | 54 | 53 |
a) Calcular el coeficiente de correlación entre las distancias (m) y los tiempos medidos en segundos.
b) Sin efectuar cálculos, razonar si debemos esperar correlación positiva o negativa entre las variables velocidad y distancia.
a)
| 100 | 11 | 10000 | 121 | 1100 | |
| 200 | 22 | 40000 | 484 | 4400 | |
| 400 | 48 | 160000 | 2304 | 19200 | |
| 800 | 114 | 640000 | 12996 | 91200 | |
| 1500 | 233 | 2250000 | 54289 | 349500 | |
| Total | 3000 | 428 | 3100000 | 70194 | 465400 |
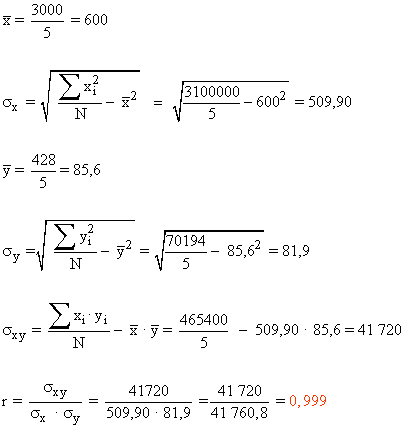
9) Dos conjuntos de datos bidimensionales tienen como coeficiente de correlación r1 = - 0,83 y r2 = 0,51.
a) Representar gráficamente dos conjuntos de puntos cuyas correlaciones reflejen aproximadamente las dadas.
b) Razonar cuál de los dos conjuntos estará más concentrado respecto a sus correspondientes rectas de regresión.
a) r1 = - 0,83 < 0 ⇒ la correlación es inversa o negativa, al aumentar la x disminuirá la y.
r1 = - 0,83, próximo a -1, la correlación es fuerte, la nube de puntos estará en una franja estrecha.
r2 = 0,51 > 0 ⇒ la correlación es directa o positiva, al aumentar el valor de x también lo hará el valor de y.
r2 = 0,51, no próximo a 1, la correlación es media-baja, la nube de puntos estará en una franja más ancha.
b) Al ser r1 = - 0,83 y r2 = 0,51 y por tanto |r1| > |r2| , el primer conjunto (correspondiente a r1) estará más concentrado respecto a las rectas de regresión de ambas.
10) Las puntuaciones en Matemáticas y Física de siete alumnos han sido las siguientes :
Matemáticas
8
8
6
7
8
6
2
Física
7
7,5
5
7
7,5
5
7
| Matemáticas | 8 | 8 | 6 | 7 | 8 | 6 | 2 |
|---|---|---|---|---|---|---|---|
| Física | 7 | 7,5 | 5 | 7 | 7,5 | 5 | 7 |
a) Halla el coeficiente de correlación de las calificaciones en Matemáticas y Física de los seis primeros alumnos.
b) Calcula el coeficiente de correlación de esas dos variables para los siete alumnos.
c) Explica la direfencia entre los resultados obtenidos.
| xi | yi | fi | fi · xi | fi · xi2 | fi · yi | fi · yi2 | xi · yi · fi |
|---|---|---|---|---|---|---|---|
| 8 | 7 | 1 | 8 | 64 | 7 | 49 | 56 |
| 8 | 7,5 | 2 | 16 | 128 | 15 | 112,5 | 120 |
| 6 | 5 | 2 | 12 | 72 | 10 | 50 | 60 |
| 7 | 7 | 1 | 7 | 49 | 7 | 49 | 49 |
Sumatorio 6 alumnos |
6 | 43 | 313 | 39 | 260,5 | 285 | |
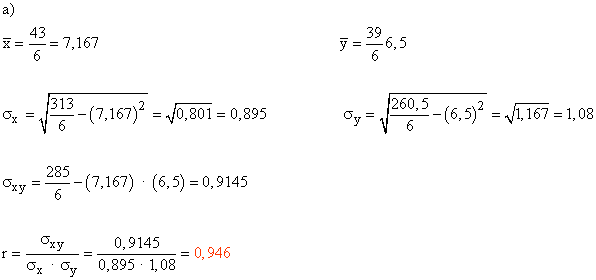
| xi | yi | fi | fi · xi | fi · xi2 | fi · yi | fi · yi2 | xi · yi · fi |
|---|---|---|---|---|---|---|---|
| 8 | 7 | 1 | 8 | 64 | 7 | 49 | 56 |
| 8 | 7,5 | 2 | 16 | 128 | 15 | 112,5 | 120 |
| 6 | 5 | 2 | 12 | 72 | 10 | 50 | 60 |
| 7 | 7 | 1 | 7 | 49 | 7 | 49 | 49 |
| 2 | 7 | 1 | 2 | 4 | 7 | 49 | 14 |
| Sumatorio 7 alumnos | 7 | 45 | 317 | 46 | 309,5 | 299 | |
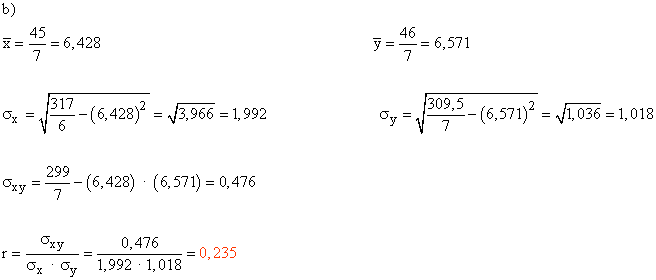
c)
En ambos casos la correlación lineal es directa, ya que el coeficiente de correlación lineal es positivo.
En el primer caso, al considerar sólo los seis primeros alumnos, obtenemos un coeficiente de correlación bastante grande, muy próximo a 1.
Sin embargo, al considerar los siete alumnos, el coeficiente de correlación es mucho más bajo, 0,235. En este caso, las variables Matemáticas y Física son aleatoriamente independientes, mientras que en el primer caso la dependencia aleatoria era fuerte.
11) La siguiente tabla ofrece los resultados de seis pares de observaciones, realizadas para analizar el grado de relación existente entre dos variables X e Y:
| X | 2 | 2 | 3 | 3 | 3 | 4 |
|---|---|---|---|---|---|---|
| Y | 0 | 1 | 1 | 2 | 4 | 3 |
Obtener:
a) Recta de regresión de Y sobre X.
b) Representación gráfica de la misma, así como de los pares de observaciones anteriores.
c) ¿Qué grado de relación lineal existe entre ambas variables?a)
2 0 4 0 0 2 1 4 1 2 3 1 9 1 3 3 2 9 4 6 3 4 9 16 12 4 3 16 9 12 Total 17 11 51 31 35
b)
c)


 INICIO
INICIO