INICIOParámetros de una distribución bidimensional
| Variable X | x1 | x2 | ... | xn |
|---|---|---|---|---|
| Variable Y | y1 | y2 | ... | yn |
Los datos de una distribución bidimensional se pueden representar en la siguiente tabla.
Los datos correspondientes a cada una de las variables se llaman datos marginales, estos nos permiten el cálculo de los parámetros marginales de cada una de las variables.
Medias marginales
Las medias marginales de cada una de las variables X e Y son, respectivamente:
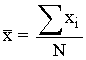
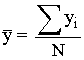
se llama centro medio de la distribución. Es el centro de gravedad (o centro de masas) de la nube de puntos. Si se tratan de medias ponderadas se llamaria centro medio ponderado.
Varianza y desviaciones típicas marginales
Las varianzas marginales , que denotamos por: 
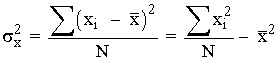
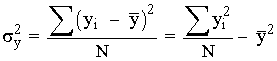
Las desviaciones típicas marginales son las raices cuadradas respectivas de la varianza.
Covarianza
La covarianza se define como la media aritmética de los productos de las diferencias de los valores de cada variable respecto de su media marginal.
En su cálculo intervienen las dos variables a la vez.
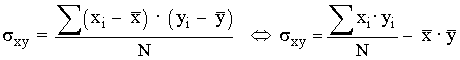
Ejemplo 1:
Se hizo una prueba a diez estudiantes para ver la relación que había entre la expresión oral (X) y la destreza manual (Y) , obteniéndose la siguiente tabla:
| X | 8 | 7 | 6 | 5 | 4 | 3 | 7 | 6 | 9 | 5 |
|---|---|---|---|---|---|---|---|---|---|---|
| Y | 5 | 5 | 6 | 7 | 8 | 7 | 4 | 5 | 3 | 5 |
a) Calcula razonadamene la media y la desviación típica de X.
b) Calcula razonablemente la media y la desviación típica de Y.
c) Calcula la covarianza
 |
 |
 |
 |
 |
|---|---|---|---|---|
| 8 | 5 | 64 | 25 | 40 |
| 7 | 5 | 49 | 25 | 35 |
| 6 | 6 | 36 | 36 | 36 |
| 5 | 7 | 25 | 49 | 35 |
| 4 | 8 | 16 | 64 | 32 |
| 3 | 7 | 9 | 49 | 21 |
| 7 | 4 | 49 | 16 | 28 |
| 6 | 5 | 36 | 25 | 30 |
| 9 | 3 | 81 | 9 | 27 |
| 5 | 5 | 25 | 25 | 25 |
| 60 | 55 | 390 | 323 | 309 |
