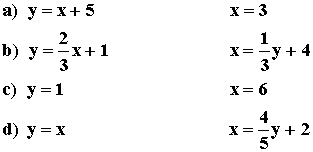1) El número de horas dedicadas al estudio de una asignatura y la calificación obtenida en el examen correspondiente a ocho personas es :
| X : horas de estudio |
20 |
16 |
34 |
23 |
27 |
32 |
18 |
22 |
| Y : calificación examen |
6,5 |
6,0 |
8,0 |
7,0 |
9,0 |
9,5 |
7,5 |
8,0 |
Se pide :
a) Recta de regresión de Y sobre X.
b) Calificación estimada para una persona que hubiese estudiado 28 horas.
2) La información estadística obtenida de una muestra de tamaño 12 sobre la relación existente entre la inversión realizada y el rendimiento obtenido en cientos de miles de euros para explotaciones agropecuarias, se muestra en el siguiente cuadro :
| Inv |
11 |
14 |
16 |
15 |
16 |
18 |
20 |
21 |
14 |
20 |
19 |
11 |
| Ren |
2 |
3 |
5 |
6 |
5 |
3 |
7 |
10 |
6 |
10 |
5 |
6 |
Se pide :
a) La recta de regresión del rendimiento respecto de la inversión.
b) La previsión de inversión que se obtendrá con un rendimiento de 1.250.000 euros.
3) La tabla nos da los gastos en electricidad y los ingresos mensuales de 6 empresas en un mes, en miles de euros. Estima el gasto en electricidad de una empresa con ingresos de 250, y explica el método utilizado.
| Gasto en electricidad |
2 |
3 |
5 |
9 |
10 |
19 |
| Ingreso total |
40 |
60 |
80 |
100 |
120 |
200 |
4) Se ha solicitado a un grupo de 50 individuos información sobre el número de horas que dedican diariamente a dormir y a ver la televisión. La clasificación de las respuestas ha permitido elaborar la siguiente tabla :
| X : Horas durmiendo |
6 |
7 |
8 |
9 |
10 |
| Y : Horas de televisión |
4 |
3 |
3 |
2 |
1 |
| fi |
3 |
16 |
20 |
10 |
1 |
Se pide :
a) Calcular el coeficiente de correlación entre X e Y.
b) Calcular la ecuación de la recta de regresión de Y sobre X.
c) Si una persona duerme ocho horas y media, ¿cuánto cabe esperar que vea la televisión?
5) Una planta envasadora de frutos secos necesita adquirir una máquina empaquetadora de bolsas de 50 gramos lo más precisa posible, para lo que efectúa una prueba de diez pesadas con cada una de las máquinas X e Y, obteniéndose los siguientes resultados en gramos :
| X |
52 |
54 |
53 |
47 |
48 |
49 |
46 |
48 |
51 |
52 |
| Y |
51 |
54 |
51 |
46 |
49 |
49 |
48 |
49 |
51 |
52 |
a) Calcular la media y la desviación típica de cada una de las distribuciones X e Y. ¿Qué máquina se debe elegir y por qué?
b) Calcular la recta de regresión de Y sobre X. ¿Qué pesada se espera de la máquina Y en una nueva prueba si se sabe que X ha dado 54 gramos?
6) La siguiente tabla muestra los índices de las Bolsas de Tokio y Madrid durante la primera semana de octubre.
| Tokio |
25721,7 |
25862,5 |
26018,3 |
26089 |
25952,3 |
| Madrid |
313 |
318,6 |
325,4 |
325,4 |
324,1 |
a) Calcular la recta de regresión de los índices de Madrid respecto de los de Tokio.
b) Calcular el coeficiente de correlación lineal y da una interpretación del resultado obtenido.
7) Un centro comercial sabe que en función de la distancia, en kilómetros, a la que se sitúe de un núcleo de población, acuden los clientes, en cientos, que figuran en la tabla :
| Nº de clientes |
8 |
7 |
6 |
4 |
2 |
1 |
| Distancia |
15 |
19 |
25 |
23 |
34 |
40 |
a) Calcular la media y desviación típica de cada una de las variables que intervienen.
b) Calcular el coeficiente de correlación.
c) Si el centro comercial se sitúa a 2 km, ¿cuántos clientes puede esperar?
d) Si desea recibir a 500 clientes, ¿a qué distancia del núcleo de población debe situarse?
8) La tabla siguiente muestra los gastos ( en miles de euros ) de cinco campañas de publicitarias junto con los consiguientes volúmenes de ventas ( en miles de euros ) obtenidos de cierto artículo. Calcular el coeficiente de correlación y la recta de regresión de la variable "Volumen de ventas" sobre la variable "Gastos de la campaña". Utilizar esta recta para predecir el volumen de venta que podría esperarse con unos gastos publicitarios de ocho mil euros. Valorar dicha predicción por el coeficiente de correlación.
| Gastos en publicidad |
2 |
3 |
5 |
6 |
10 |
| Volumen de ventas |
50 |
60 |
120 |
150 |
180 |
9) Observados un grupo de 25 personas, los ingresos anuales X en miles de euros ) y los impuestos pagados ( Y en miles de euros ), se registraron los siguientes datos, de donde se obtiene que la cantidad media de ingresos son 424.000 euros, con desviación típica 145.000 :
| X / Y |
( 1, 2 ] |
( 2, 4 ] |
( 4, 6 ] |
| ( 0, 200 ] |
2 |
0 |
0 |
| ( 200, 600 ] |
8 |
10 |
1 |
| ( 600, 800 ] |
0 |
0 |
4 |
a) Calcular los impuestos medios.
b) Estudiar el grado de correlación lineal existente entre ambas variables.
c) Obtener una recta de regresión para explicar los impuestos en función de los ingresos. Si una persona tiene unos ingresos de 550.000 euros, ¿qué cantidad deberá pagar en concepto de impuestos?
10) En la siguiente gráfica se presenta la evolución anual de la flota pesquera española con respeto al año 1977. Las variables estudiadas son el número de embarcaciones, su tonelaje y el número de tripulantes.
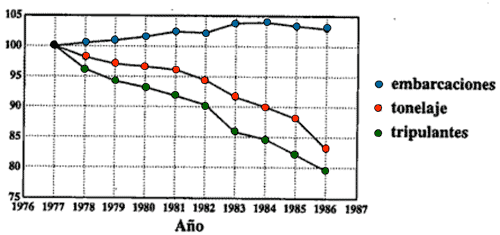
Nos dicen que y = 23,64 + 0,78x ; -0,79 ; 0,97 ; y = 386,43 - 2,87x son las respuestas desordenadas de :
a) Coeficiente de correlación entre tripulantes y embarcaciones.
b) Coeficiente de correlación entre tripulantes y tonelaje.
c) La recta de regresión de tripulantes ( Y ) sobre embarcaciones ( X ).
d) La recta de regresión de tripulantes ( Y ) sobre tonelaje ( X ).
Dar la respuesta correcta de cada uno de los apartados explicando la asignación elegida.
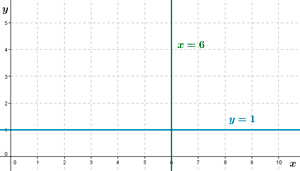
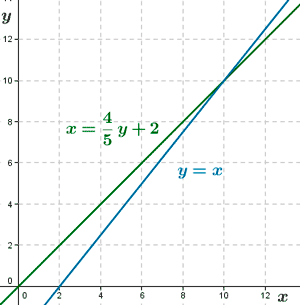
11) Las rectas de regresión de cuatro distribuciones bidimensionales son las siguientes :
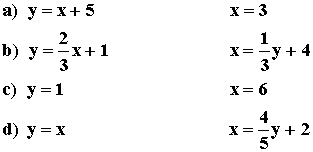
Indica en qué casos es significativa la correlación lineal.
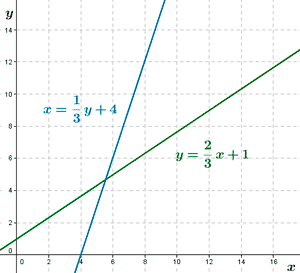
12) Halla el centro medio de una distribución sabiendo que sus rectas de regresión valen :
De Y sobre X : y = x + 5.
De X sobre Y : x = 0,25y - 0,1.
13) El coeficiente de determinación de una distribución cuya nube de puntos se ajusta a una recta es igual a 0,33.
a) Interpreta este resultado.
b) ¿Tiene sentido encontrar un modelo lineal para esta distribución que permita realizar estimaciones?
14) Si el coeficiente de correlación vale r = 0,7.
a) ¿Qué tanto por ciento de la variación de Y es debido a la variación de X usando el modelo de regresión lineal?
b) ¿Tiene sentido realizar estimaciones en la recta de regresión obtenida?
15) Se midieron los valores de concentración en microgramos por centímetro cúbico de una sustancia A en un suero fetal y los valores de su concentración en suero materno. Se obtuvieron los siguientes datos en una muestra de seis embarazadas al final de la gestación:
| Concentración suero madre (X) |
8 |
4 |
12 |
2 |
7 |
9 |
| Concentración suero feto (Y) |
6 |
4 |
8 |
1 |
4 |
5 |
a) Calcula el coeficiente de correlación lineal.
b) Halla la recta que permita estimar los valores fetales a partir de los maternos.
c) Halla el coeficiente de determinación e interprétalo para estudiar la bondad del ajuste.
16) En cierto país, el tipo de interés y el índice de la Bolsa en los últimos seis meses vienen dados por la siguiente tabla :
| Tipo de interés ( % ) |
8 |
7,5 |
7,2 |
6 |
5,5 |
5 |
| Índice |
120 |
130 |
134 |
142 |
150 |
165 |
Halla el índice previsto de la Bolsa en el séptimo mes, suponiendo que el tipo de interés en ese mes fue del 4,1 % y analiza la fiabilidad de la predicción, según el valor del coeficiente de correlación.
17) Al medir la pérdida de actividad de un preparado hormonal en el curso del tiempo, se obtuvo el resultado registrado en esta tabla :
| Tiempo ( meses ) |
1 |
2 |
3 |
4 |
5 |
| % actividad restante |
90 |
75 |
42 |
30 |
21 |
a) ¿Qué tanto por ciento de actividad restante quedará a los seis meses?
b) ¿Cuánto tiempo habrá de transcurrir para que quede el 50 % de actividad restante?
1) El número de horas dedicadas al estudio de una asignatura y la calificación obtenida en el examen correspondiente a ocho personas es :
| X : horas de estudio |
20 |
16 |
34 |
23 |
27 |
32 |
18 |
22 |
| Y : calificación examen |
6,5 |
6,0 |
8,0 |
7,0 |
9,0 |
9,5 |
7,5 |
8,0 |
Se pide :
a) Recta de regresión de Y sobre X.
b) Calificación estimada para una persona que hubiese estudiado 28 horas.
| xi |
yi |
xi2 |
yi2 |
xi · yi |
| 16 |
6 |
256 |
36 |
96 |
| 18 |
7,5 |
324 |
56,25 |
135 |
| 20 |
6,5 |
400 |
42,25 |
130 |
| 22 |
8 |
484 |
64 |
176 |
| 23 |
7 |
529 |
49 |
161 |
| 27 |
9 |
729 |
81 |
243 |
| 32 |
9,5 |
1024 |
90,25 |
304 |
| 34 |
8,5 |
1156 |
72,25 |
289 |
| 192 |
62 |
4902 |
491 |
1534 |

2) La información estadística obtenida de una muestra de tamaño 12 sobre la relación existente entre la inversión realizada y el rendimiento obtenido en cientos de miles de euros para explotaciones agropecuarias, se muestra en el siguiente cuadro :
| Inv |
11 |
14 |
16 |
15 |
16 |
18 |
20 |
21 |
14 |
20 |
19 |
11 |
| Ren |
2 |
3 |
5 |
6 |
5 |
3 |
7 |
10 |
6 |
10 |
5 |
6 |
Se pide :
a) La recta de regresión del rendimiento respecto de la inversión.
b) La previsión de inversión que se obtendrá con un rendimiento de 1.250.000 euros.
| xi |
yi |
xi2 |
yi2 |
xi · yi |
| 11 |
2 |
121 |
4 |
22 |
| 14 |
3 |
196 |
9 |
42 |
| 16 |
5 |
256 |
25 |
80 |
| 15 |
6 |
225 |
36 |
90 |
| 16 |
5 |
256 |
25 |
80 |
| 18 |
3 |
324 |
9 |
54 |
| 20 |
7 |
400 |
49 |
140 |
| 21 |
10 |
441 |
100 |
210 |
| 14 |
6 |
196 |
36 |
84 |
| 20 |
10 |
400 |
100 |
200 |
| 19 |
5 |
361 |
25 |
95 |
| 11 |
6 |
121 |
36 |
66 |
| 195 |
68 |
3297 |
454 |
1163 |

3) La tabla nos da los gastos en electricidad y los ingresos mensuales de 6 empresas en un mes, en miles de euros. Estima el gasto en electricidad de una empresa con ingresos de 250, y explica el método utilizado.
| Gasto en electricidad |
2 |
3 |
5 |
9 |
10 |
19 |
| Ingreso total |
40 |
60 |
80 |
100 |
120 |
200 |
| xi |
yi |
xi2 |
yi2 |
xi · yi |
| 2 |
40 |
4 |
1600 |
80 |
| 3 |
60 |
9 |
3600 |
180 |
| 5 |
80 |
25 |
6400 |
400 |
| 9 |
100 |
81 |
10000 |
900 |
| 10 |
120 |
100 |
14400 |
1200 |
| 19 |
200 |
361 |
40000 |
3800 |
| 48 |
600 |
580 |
76000 |
6560 |

4) Se ha solicitado a un grupo de 50 individuos información sobre el número de horas que dedican diariamente a dormir y a ver la televisión. La clasificación de las respuestas ha permitido elaborar la siguiente tabla :
| X : Horas durmiendo |
6 |
7 |
8 |
9 |
10 |
| Y : Horas de televisión |
4 |
3 |
3 |
2 |
1 |
| fi |
3 |
16 |
20 |
10 |
1 |
Se pide :
a) Calcular el coeficiente de correlación entre X e Y.
b) Calcular la ecuación de la recta de regresión de Y sobre X.
c) Si una persona duerme ocho horas y media, ¿cuánto cabe esperar que vea la televisión?
| xi |
yi |
fi |
xi · fi |
yi · fi |
xi2 |
yi2 |
fi · xi2 |
fi · yi2 |
fi · xi · yi |
| 6 |
4 |
3 |
18 |
12 |
36 |
16 |
108 |
48 |
72 |
| 7 |
3 |
16 |
112 |
48 |
49 |
9 |
784 |
144 |
336 |
| 8 |
3 |
20 |
160 |
60 |
64 |
9 |
1280 |
180 |
480 |
| 9 |
2 |
10 |
90 |
20 |
81 |
4 |
810 |
40 |
180 |
| 10 |
1 |
1 |
10 |
1 |
100 |
1 |
100 |
1 |
10 |
| |
|
50 |
390 |
141 |
|
|
3082 |
413 |
1078 |
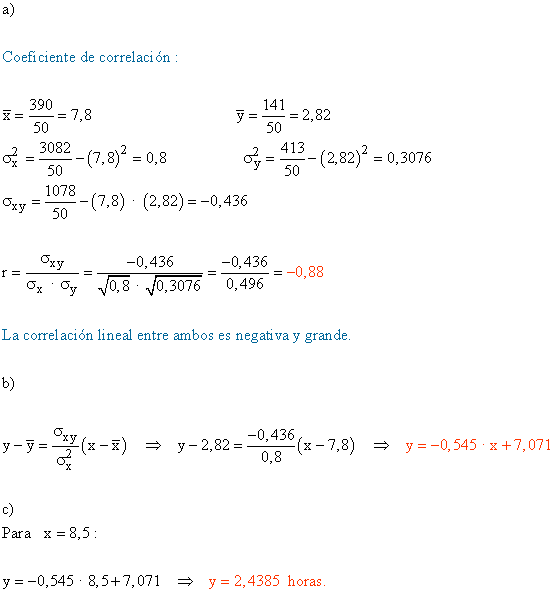
5) Una planta envasadora de frutos secos necesita adquirir una máquina empaquetadora de bolsas de 50 gramos lo más precisa posible, para lo que efectúa una prueba de diez pesadas con cada una de las máquinas X e Y, obteniéndose los siguientes resultados en gramos :
| X |
52 |
54 |
53 |
47 |
48 |
49 |
46 |
48 |
51 |
52 |
| Y |
51 |
54 |
51 |
46 |
49 |
49 |
48 |
49 |
51 |
52 |
a) Calcular la media y la desviación típica de cada una de las distribuciones X e Y. ¿Qué máquina se debe elegir y por qué?
b) Calcular la recta de regresión de Y sobre X. ¿Qué pesada se espera de la máquina Y en una nueva prueba si se sabe que X ha dado 54 gramos?
| xi |
yi |
xi2 |
yi2 |
xi · yi |
| 52 |
51 |
2704 |
2601 |
2652 |
| 54 |
54 |
2916 |
2916 |
2916 |
| 53 |
51 |
2809 |
2601 |
2703 |
| 47 |
46 |
2209 |
2116 |
2162 |
| 48 |
49 |
2304 |
2401 |
2352 |
| 49 |
49 |
2401 |
2401 |
2401 |
| 46 |
48 |
2116 |
2304 |
2208 |
| 48 |
49 |
2304 |
2401 |
2352 |
| 51 |
51 |
2601 |
2601 |
2601 |
| 52 |
52 |
2704 |
2704 |
2704 |
| 500 |
500 |
25068 |
25046 |
25051 |

6) La siguiente tabla muestra los índices de las Bolsas de Tokio y Madrid durante la primera semana de octubre.
| Tokio |
25721,7 |
25862,5 |
26018,3 |
26089 |
25952,3 |
| Madrid |
313 |
318,6 |
325,4 |
325,4 |
324,1 |
a) Calcular la recta de regresión de los índices de Madrid respecto de los de Tokio.
b) Calcular el coeficiente de correlación lineal y da una interpretación del resultado obtenido.
| xi |
yi |
xi2 |
yi2 |
xi · yi |
| 25721,7 |
313 |
661605851 |
97969 |
8050892.1 |
| 25862.5 |
318,6 |
668868906 |
101505,96 |
8239792.5 |
| 26018,3 |
325,4 |
6766951935 |
105885,16 |
8466354,82 |
| 26089 |
325,4 |
680635921 |
105885,16 |
8489360,6 |
| 25952,3 |
324,1 |
673521875 |
105040,81 |
8411140,43 |
| 129643,8 |
1606,5 |
3361584488 |
516286,09 |
41657540,5 |

7) Un centro comercial sabe que en función de la distancia, en kilómetros, a la que se sitúe de un núcleo de población, acuden los clientes, en cientos, que figuran en la tabla :
| Nº de clientes |
8 |
7 |
6 |
4 |
2 |
1 |
| Distancia |
15 |
19 |
25 |
23 |
34 |
40 |
a) Calcular la media y desviación típica de cada una de las variables que intervienen.
b) Calcular el coeficiente de correlación.
c) Si el centro comercial se sitúa a 2 km, ¿cuántos clientes puede esperar?
d) Si desea recibir a 500 clientes, ¿a qué distancia del núcleo de población debe situarse?
| xi |
yi |
xi2 |
yi2 |
xi · yi |
| 8 |
15 |
64 |
225 |
120 |
| 7 |
19 |
49 |
361 |
133 |
| 6 |
25 |
36 |
625 |
150 |
| 4 |
23 |
16 |
529 |
92 |
| 2 |
34 |
4 |
1156 |
68 |
| 1 |
40 |
1 |
1600 |
40 |
| 28 |
156 |
170 |
4496 |
603 |

8) La tabla siguiente muestra los gastos ( en miles de euros ) de cinco campañas de publicitarias junto con los consiguientes volúmenes de ventas ( en miles de euros ) obtenidos de cierto artículo. Calcular el coeficiente de correlación y la recta de regresión de la variable "Volumen de ventas" sobre la variable "Gastos de la campaña". Utilizar esta recta para predecir el volumen de venta que podría esperarse con unos gastos publicitarios de ocho mil euros. Valorar dicha predicción por el coeficiente de correlación.
| Gastos en publicidad |
2 |
3 |
5 |
6 |
10 |
| Volumen de ventas |
50 |
60 |
120 |
150 |
180 |
| xi |
yi |
xi2 |
yi2 |
xi · yi |
| 2 |
50 |
4 |
2500 |
100 |
| 3 |
60 |
9 |
3600 |
180 |
| 5 |
120 |
25 |
14400 |
600 |
| 6 |
150 |
36 |
22500 |
900 |
| 10 |
180 |
100 |
32400 |
1800 |
| 26 |
560 |
174 |
75400 |
3580 |

9) Observados un grupo de 25 personas, los ingresos anuales X en miles de euros ) y los impuestos pagados ( Y en miles de euros ), se registraron los siguientes datos, de donde se obtiene que la cantidad media de ingresos son 424.000 euros, con desviación típica 145.000 :
| X / Y |
( 1, 2 ] |
( 2, 4 ] |
( 4, 6 ] |
| ( 0, 200 ] |
2 |
0 |
0 |
| ( 200, 600 ] |
8 |
10 |
1 |
| ( 600, 800 ] |
0 |
0 |
4 |
a) Calcular los impuestos medios.
b) Estudiar el grado de correlación lineal existente entre ambas variables.
c) Obtener una recta de regresión para explicar los impuestos en función de los ingresos. Si una persona tiene unos ingresos de 550.000 euros, ¿qué cantidad deberá pagar en concepto de impuestos?
Tomamos las marcas de clase de cada intervalo y reunimos los datos en la siguiente tabla :
| xi |
yi |
fi |
fi · xi |
fi · yi |
xi2 |
yi2 |
fi · xi2 |
fi · yi2 |
fi · xi · yi |
| 1,5 |
100 |
2 |
200 |
3 |
10000 |
2,25 |
20000 |
4,5 |
300 |
| 1,5 |
400 |
8 |
3200 |
12 |
160000 |
2,25 |
1280000 |
18 |
4800 |
| 3 |
400 |
10 |
4000 |
30 |
160000 |
9 |
1600000 |
90 |
12000 |
| 5 |
400 |
1 |
400 |
5 |
160000 |
25 |
160000 |
25 |
2000 |
| 5 |
700 |
4 |
2800 |
20 |
490000 |
25 |
1960000 |
100 |
14000 |
| |
|
25 |
106000 |
70 |
|
|
5020000 |
237,5 |
33100 |

10) En la siguiente gráfica se presenta la evolución anual de la flota pesquera española con respeto al año 1977. Las variables estudiadas son el número de embarcaciones, su tonelaje y el número de tripulantes.

Nos dicen que y = 23,64 + 0,78x ; -0,79 ; 0,97 ; y = 386,43 - 2,87x son las respuestas desordenadas de :
a) Coeficiente de correlación entre tripulantes y embarcaciones.
b) Coeficiente de correlación entre tripulantes y tonelaje.
c) La recta de regresión de tripulantes ( Y ) sobre embarcaciones ( X ).
d) La recta de regresión de tripulantes ( Y ) sobre tonelaje ( X ).
Dar la respuesta correcta de cada uno de los apartados explicando la asignación elegida.
Obervando la gráfica podemos observar que a medida que el número de embarcaciones fue creciendo, tanto como el tonelaje y los tripulantes, fue disminuyendo. Entre embarcaciones y tripulantes, existe por tanto una correlación lineal negativa o inversa, siendo así la recta de regresión decreciente. Por otro lado, a medida que pasan los años tanto tripulantes como tonelaje van disminuyendo. Su correlación lineal es entonces positiva, teniendo además una recta regresión cuyo coeficiente es positivo.
De todo esto podemos deducir :
a) El coeficiente de correlación entre tripulantes y embarcaciones es : - 0,79.
b) El coeficiente de correlación entre tripulantes y tonelaje es : 0,97.
c) La recta de regresión de tripulantes sobre embarcaciones es : y = 386,43 - 2,87x.
d) La recta de regresión de tripulantes sobre tonelaje es : y = 23,64 + 0,78x.
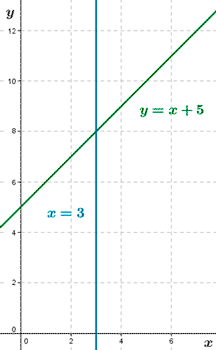
12) Halla el centro medio de una distribución sabiendo que sus rectas de regresión valen :
De Y sobre X : y = x + 5.
De X sobre Y : x = 0,25y - 0,1.

13) El coeficiente de determinación de una distribución cuya nube de puntos se ajusta a una recta es igual a 0,33.
a) Interpreta este resultado.
b) ¿Tiene sentido encontrar un modelo lineal para esta distribución que permita realizar estimaciones?
a)
Si r 2 = 0,33 signifa que el 33% de las variación de Y se debe a la variación de X si usamos regresión lineal. Mientras que el 67% restante de la variación de Y se debe al azar o a la influencia sobre Y de otras variables distintas de X.
b)
Que el coeficiente de relación sea r 2 = 0,33 implica que el coeficiente de correlación es r = ± 0,57 , lo que nos indica que se trata de una dependencia aleatoria media-baja. Por tanto le modelo lineal tan sólo tendrá sentido cuando realicemos estimaciones en puntos muy cercanos a 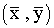
14) Si el coeficiente de correlación vale r = 0,7.
a) ¿Qué tanto por ciento de la variación de Y es debido a la variación de X usando el modelo de regresión lineal?
b) ¿Tiene sentido realizar estimaciones en la recta de regresión obtenida?
a)
El coeficiente de determinación será r 2 = 0,72 = 0,49 , lo que nos indica que un 49% de la variación de Y es debida a la variación de X.
b)
En este ejemplo, el coeficiente de correlación vale 0,7 lo que nos indica que esta distribución presenta una dependencia intermedia-fuerte, y las estimaciones que realicemos con la recta de regresión sólo tendrán sentido si se hacen para puntos cercanos al centro de gravedad de la distribución : 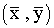
16) En cierto país, el tipo de interés y el índice de la Bolsa en los últimos seis meses vienen dados por la siguiente tabla :
| Tipo de interés ( % ) |
8 |
7,5 |
7,2 |
6 |
5,5 |
5 |
| Índice |
120 |
130 |
134 |
142 |
150 |
165 |
Halla el índice previsto de la Bolsa en el séptimo mes, suponiendo que el tipo de interés en ese mes fue del 4,1 % y analiza la fiabilidad de la predicción, según el valor del coeficiente de correlación.

17) Al medir la pérdida de actividad de un preparado hormonal en el curso del tiempo, se obtuvo el resultado registrado en esta tabla :
| Tiempo ( meses ) |
1 |
2 |
3 |
4 |
5 |
| % actividad restante |
90 |
75 |
42 |
30 |
21 |
a) ¿Qué tanto por ciento de actividad restante quedará a los seis meses?
b) ¿Cuánto tiempo habrá de transcurrir para que quede el 50 % de actividad restante?
Construimos en primer lugar la tabla de frecuencias asociada a dichos datos.
| xi |
yi |
xi2 |
yi2 |
xi · yi |
| 1 |
90 |
1 |
8100 |
90 |
| 2 |
75 |
4 |
5625 |
150 |
| 3 |
42 |
9 |
1764 |
125 |
| 4 |
30 |
16 |
900 |
120 |
| 5 |
21 |
25 |
441 |
105 |
| 15 |
258 |
55 |
16830 |
591 |





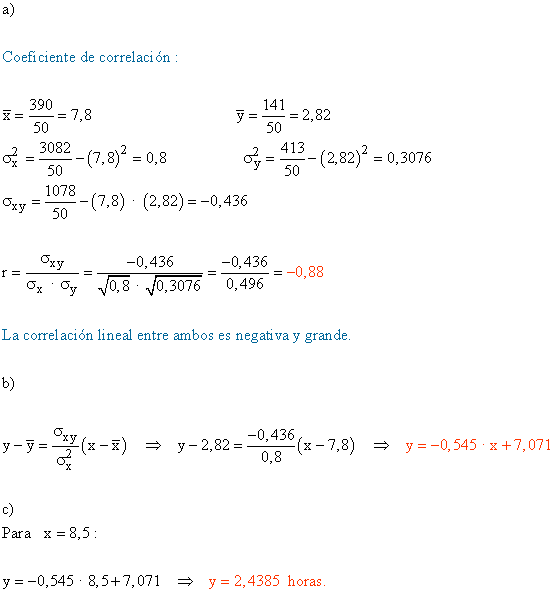







![]()
![]()
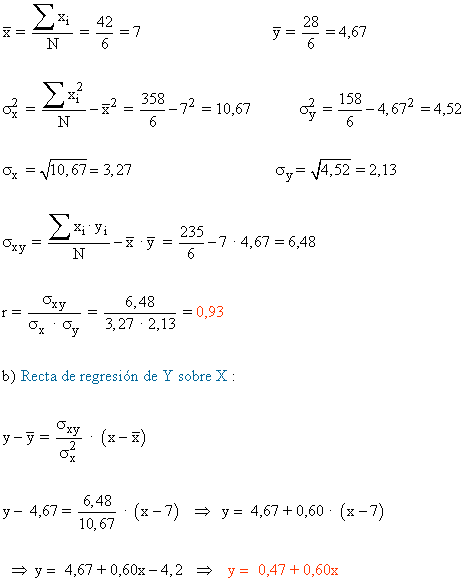




 INICIO
INICIO