Pendiente de una recta.

La pendiente m de una recta y = mx es la medida de su crecimiento y mide la inclinación de la recta respecto al eje positivo de abcisas.

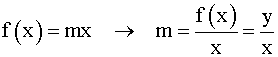
Si m es positiva, la recta es creciente ; si m es negativa la recta es decreciente.

Una función lineal o de proporcionalidad directa es :

Creciente : si la constante de proporcionalidad es positiva ( m > 0 ).

Decreciente : si la constante de proporcionalidad es negativa ( m< 0 ).

Función creciente.

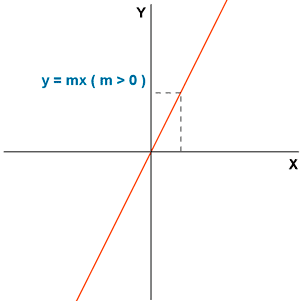
funcion lineal o de proporcionalidad directa creciente

Función decreciente.

funcion lineal o de proporcionalidad directa decreciente

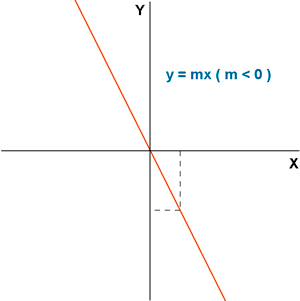
Ejemplo 1 :

Representa gráficamente las siguientes funciones lineales y determina la pendiente de cada una de ellas. Indica si son crecientes o decrecientes.
a)    y = 2x
b)    y = - 3x
c)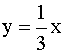

x = -1    →    y = 2 · ( - 1 ) = - 2
x = 0    →    y = 2 · ( 0 ) = 0
x = 1    →    y = 2 · 1 = 2
x= 2    →    y = 2 · 2 = 4

x	y
- 1	- 2
0	0
1	2
2	4

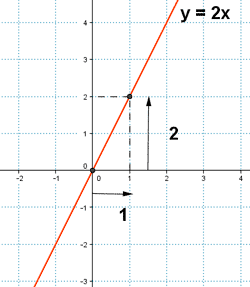
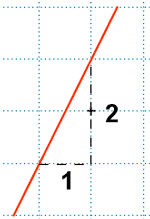
Su pendiente es 2 = 2 / 1.
Cuando la x avanza una unidad, la y sube dos unidades.
Aumenta la x, aumenta la y, luego la función es creciente.

x = - 1    →    y = - 3 · ( - 1 ) = 3
x = 0    →    y = - 3 · 0 = 0
x = 1    →    y = - 3 · 1 = - 3
x = 2    →    y = - 3 · ( 2 ) = - 6

x	y
- 1	3
0	0
1	- 3
2	- 6

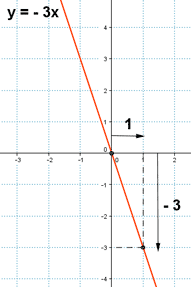
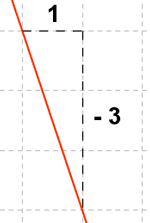
Su pendiente es - 3 = - 3 / 1.
Cuando x avanza una unidad, la y baja tres unidades.
Aumenta la x pero disminuye la y, l función es decreciente.

x = 0 → y = 1 / 3 · ( 0 ) = 0
x = 1 → y = 1 / 3 · 1 = 1 / 3
x = 2 → y = 1 / 3 · 2 = 2 / 3
x = 3 → y = 1 / 3 · 3 = 1

x	y
0	0
1	1 / 3
2	2 / 3
3	1

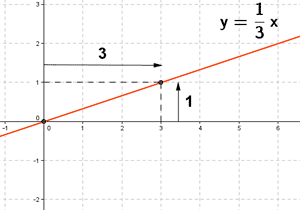
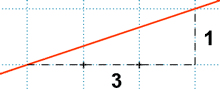
Su pendiente es 1 / 3 = 1 / 3.
Cuando x avanza tres unidades, la y sube una unidad.
Aumenta la x, aumenta la y, luego la función es creciente.