Fracciones algebraicas
Una fración algebraica es el cociente de dos polinomios, siendo el denominador un polinomio no nulo.
![]()
Ejemplo de simplificación de fracciones algebraicas
Son fracciones algebraicas:
![]()
No son fracciones algebraicas:
![]()
Fracciones equivalentes
Decimos que dos fracciones son equivalentes si los productos cruzados son iguales.
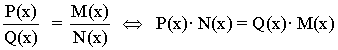
Ejemplo de fracciones equivalentes
![]()
Son equivalentes puesto que: (x2 - 4)(x2 + 2x + 4) = x4 + 2x3 - 8x - 16 = (x + 2)(x3 - 8)
Propiedad fundamental de las fracciones algebraicas
Si multiplicamos o dividimos el numerador y el denominador de una fracción algebraica por un mismo polinomio, distinto del nulo, resulta una fracción algebraica equivalente a la inicial.
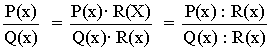
Ejemplo
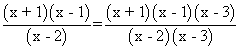
Simplificación de fracciones algebraicas
Simplificar una fracción algebraica es obtener otra fracción más sencilla.
Se descomponen el numerador y denominador como producto de factores irreductibles y se eliminan los factores comunes.
También se pueden dividir el numerador y el denominador entre el máximo común divisor (MCD) de ambos.
Ejemplo de simplificación de fracciones algebraicas
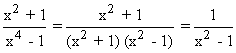
Error algebraico
Al simplificar una fracción algebraica no debemos cometer los siguientes errores algebraicos:


Sólo podemos simplificar cuando se trata de un producto de términos.


 INICIO
INICIO

