Teorema del resto y teorema del factor

Teorema del resto

El resto de la división de un polinomio P(x) por   ( x - a )   es igual al valor numérico de dicho polinomio en    x = a  .

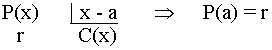
Demostración teorema del resto

P(x) = (x - a) · C(x) + r

Si hacemnos x = a

P(a) = (a - a) · C(a) + r = r

Haya el valor numérico del polinomio   P(x) = x³ - 5x² - x - 1   para   x = 2 .

a) Utilizando la definición del valor numérico.

P(2) = 2³ - 5 · 2² - 2 - 1 = 8 - 20 - 2 - 1 = -15

b) Haciendo la división.

(x³ - 5x² - x - 1) : (x - 2)

Para dividir entre   (x - 2),   utilizamos la regla de Ruffini.

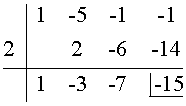
Por tanto,   r = - 15 = P(2)    TEOREMA DEL RESTO

Teorema del factor

Un polinomio   P(x)   tiene como factor   ( x - a)   , o se dice que es divisible por el binomio    ( x - a)   , si el valor numérico de dicho polinomio para    x = a    es cero.



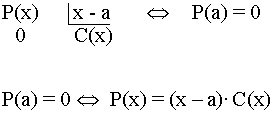
Al número    a    se le llama raíz del polinomio P(x).

Las raices enteras de un polinomio son divisores del término independiente siempre que este no sea nulo.

Comprueba si   -1   y   3   son raices del polinomio   P(x) = x³ - 27   y factoriza dicho polinomio

Divisores de 27 = Div(27) = {1, -1, 3, -3, 9, -9, 27, -27}

P(-1) = (-1)³ - 27 = -28        -1 no es raiz de P(x)

P(3) = 3³ - 27 = 0                  3 si es raiz de P(x)

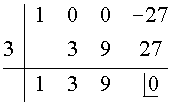
De esta forma se cumple que:

P(x) = x³ - 27 = (x - 3) · (x² + 3x + 9)