Ejercicios resueltos de polinomios
1) Suma y resta de polinomios:
1) Calcula las siguientes sumas para los siguientes polinomios:
P(x) = 5x2 - 7x + 3
Q(x) = -5x2 + 2x
R(x) = x3 + x2 + 2
a) P(x) + Q(x)
a) P(x) + Q(x) = 5x2 - 7x + 3 - 5x2 + 2x =
= 5x2 - 5x2 - 7x + 2x + 3 = -5x + 3
b) P(x) + R(x))
b) P(x) + R(x) = 5x2 - 7x + 3 + x3 + x2 + 2 =
= x3 + 5x2 + x2 - 7x + 3 + 2 = x3 + 6x2 - 7x + 5
c) Q(x) + R(x)
c) Q(x) + R(x) = -5x2 + 2x + x3 + x2 + 2 =
= x3 - 5x2 + x2 + 2x + 2 = x3 - 4x2 + 2x + 2
2) Hallar el polinomio diferencia entre:
a) P(x) = x4 + x2 + 2 y Q(x) = x3 - 2x2 - 5x + 6
a) P(x) - Q(x) = x4 + x2 + 2 - (x3 - 2x2 - 5x + 6) =
= x4 + x2 + 2 - x3 + 2x2 + 5x - 6 = x4 - x3 + 3x2 + 5x - 4
b) P(x) = x3 + x2 - x + 1 y Q(x) = 2x2 + 3x + 4
b) P(x) - Q(x) = x3 + x2 - x + 1 - (2x2 + 3x + 4) =
= x3 + x2 - x + 1 - 2x2 - 3x - 4 = x3 - x2 - 4x - 3
c) P(x) = x5 - 2x3 + 4x2 - 6 y Q(X) = x5 + x4 + 3x2 + 4x + 5
c) P(x) - Q(x) = x5 - 2x3 + 4x2 - 6 - (x5 + x4 + 3x2 + 4x + 5) =
= x5 - 2x3 + 4x2 - 6 - x5 - x4 - 3x2 - 4x - 5 = -x4 - 5x3 + x2 - 4x - 11
3) Calcula y simplifica:
a) (x2 - 5x + 1) - (3x - 1) + (2x2 + 3x - 1) - (x3 + 2x - 5)
(x2 - 5x + 1) - (3x - 1) + (2x2 + 3x - 1) - (x3 + 2x - 5) =
= x2 - 5x + 1 - 3x + 1 + 2x2 + 3x - 1 - x3 - 2x + 5 = -x3 + 3x2 - 7x + 6
4) Sean P(x) = x2 - 4x + 2 y Q(x) = 2x3 + x2 + 5. Calcular:
a) -2P(x)
a) -2P(x) = -2(x2 - 4x + 2) = - 2x2 + 8x - 4
b) 4Q(x)
b) 4Q(x) = 4(2x3 + x2 + 5) = 8x3 + 4x2 + 20
c) 3P(x) - 2Q(x)
c) 3P(x) - 2Q(x) = 3(x2 - 4x + 2) - 2(2x3 + x2 + 5) =
= 3x2 - 12x + 6 - 4x3 - 2x2 - 10 = -4x3 + x2 - 12x - 4
También podemos resolverlo de esta otra forma:
3P(x) = 3x2 - 12x + 6
-2Q(x) = - 4x3 - 2x2 - 10
________________________________
3P(x) - 2Q(x) = - 4x3 + x2 - 12x - 4
2) Multiplicación de polinomios:
1) Hallar los siguientes productos:
a) (-2x2)(x5 - 4x2 + 3x + 1)
a) (-2x2)(x5 - 4x2 + 3x + 1) = - 2x7 + 8x4 - 6x3 - 2x2
b) (x2 - 1)(5x5)
b) (x2 - 1)(5x5) = 5x7 - 5x5
c) (-3x3)(2x4 - 3x3 + 2x - x + 3)
c) (-3x3)(2x4 - 3x3 + 2x - x + 3) = - 6x7 + 9x6 - 6x4 + 3x4 - 9x3
2) Hallar los siguientes productos:
a) P(x) = 5x2 + 3x - 1 y Q(x) = x + 2
a) P(x)·Q(x) = (5x2 + 3x - 1)·(x + 2) = (5x2 + 3x - 1)x + (5x2 + 3x - 1)2 =
= 5x3 + 3x2 - x + 102 + 6x - 2 = 5x3 + 13x2 + 5x - 2
b) P(x) = x3 + 1 y Q(x) = x2 + x + 1
b) P(x)·Q(x) = (x3 + 1)·(x2 + x + 1) = x3(x2 + x + 1) + (x2 + x + 1) = x5 + x4 + x3 + x2 + x + 1
c) P(x) = x3 + 2x2 + x + 1 y Q(x) = x2 - 1
c) P(x)·Q(x) = (x3 + 2x2 + x + 1)·(x2 - 1) = (x3 + 2x2 + x + 1)x2 - (x3 + 2x2 + x + 1) =
= x5 + 2x4 + x3 + x2 - x3 - 2x2 - x - 1 = x5 + 2x4 - x2 - x - 1
d) P(x) = - x3 + 4x - 3 y Q(x) = x2 + 3x + 4
d) P(x)·Q(x) = (- x3 + 4x - 3)·(x2 + 3x + 4) = - x3(x2 + 3x + 4) + 4x(x2 + 3x + 4) - 3(x2 + 3x + 4) =
= - x5 - 3x4 - 4x3 + 4x3 + 12x2 + 16x - 3x2 - 9x - 12 = - x5 - 3x4 + 9x2 + 7x - 12
También podemos resolverlo de la siguiente manera:
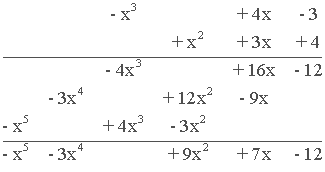
3) División de polinomios:
1) Efectua las siguientes divisiones indicando cual es el polinomio cociente y el polinomio resto:
a) (x3 + 4x2 + 6) : (x - 4)
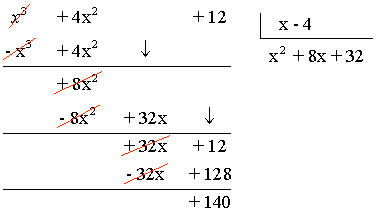
Por tanto, C(x) = x2 + 8x + 32 R(x) = 140
b) (x3 - 1) : (x - 1)
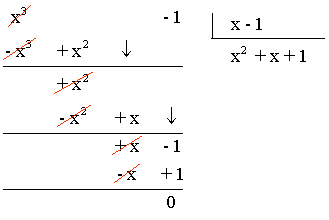
Por tanto, C(x) = x2 + x + 1 R(x) = 0
c) (4x3 - 8x2 - 9x + 10) : (2x - 3)
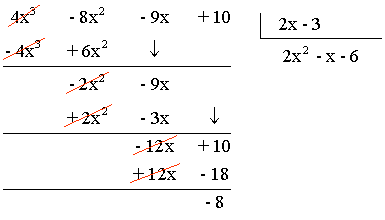
Por tanto, C(x) = 2x2 - x - 6 R(x) = - 8
4) División de polinomios:
1) Realiza la siguientes divisiones:
a) (6x4 + 4x3 + 2x2 + x - 2) : (3x2 + x - 1)
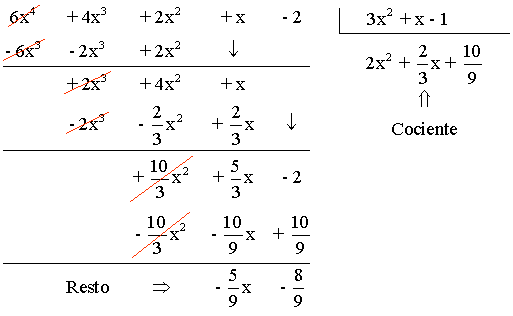
b) (x6 - 3x2 + 5x - 8) : (x2 - 3x + 1)
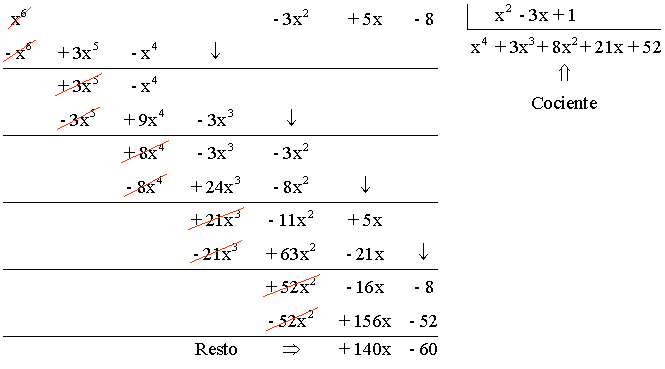
c) (x5 - x3 + x) : (x2 + 1)
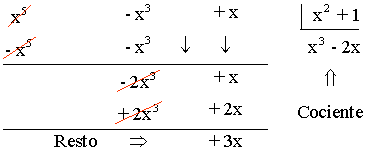
5) División exacta de polinomios:
1) Determina los coeficientes a y b para que el polinomio (x3 + ax2 + bx + 5) sea divisible por (x2 + x + 1)
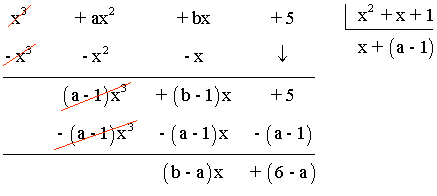
Para que la división sea exacta el resto de dicha división tiene que ser igual a 0.
Por lo tanto se debe cumplir las dos siguientes condiciones:
b - a = 0
6 - a = 0
Eso ocurre si y solo si a = 6 y b = 6


 INICIO
INICIO