Ejercicios resueltos de factorización de polinomios

Hallar las raíces enteras de los siguientes polinomios:

1)   x³ + 2x² - x - 2

Las raíces enteras se encuentran entre los divisores del término independiente del polinomio:   ±1   y   ±2.

P(1) = 1³ + 2·1² - 1 - 2 = 1 + 2 - 1 - 2 = 0

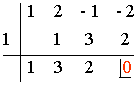
P(-1) = (-1)³ + 2·(-1)² -(-1) - 2 = -1 + 2 + 1 - 2 = 0

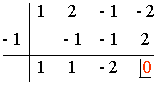
P(2) = 2³ + 2·2² - 2 - 2 = 8 + 8 - 2 - 2 = 12

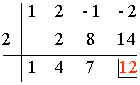
P(-2) = (-2)³ + 2·(-2)² - (- 2) - 2 = -8 + 8 + 2 - 2 = 0

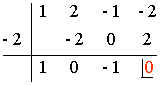
Por lo tanto, las raíces enteras del polinomio son   + 1 ,   - 1   y   - 2.

2)   x³ + 3x² - 4x - 12

Las raíces enteras se encuentran entre los divisores del término independiente del polinomio:   ±1 ,   ±2 ,   ±3 ,  ±4 ,  ±6   y   ±12.

P(2) = 2³ + 3·2² - 4·2 - 12 = 8 + 12 - 8 - 12 = 0

P(-2) = (-2)³ + 3·(-2)² - 4·(-2) - 12 = -8 + 12 + 8 - 12 = 0

P(-3) = (-3)³ + 3·(-3)² - 4·(-3) - 12 = -27 + 27 + 12 - 12 = 0

Por lo tanto, las raíces enteras del polinomio son   + 2 ,   - 2   y   - 3.

3)   x⁵ + x⁴ - 16x - 16

Las raíces enteras se encuentran entre los divisores del término independiente del polinomio:   ±1 ,   ±2 ,   ±4 ,  ±8   y   ±16.

P(-1) = (-1)⁵ + (-1)⁴ - 16·(-1) - 16 = -1 + 1 + 16 - 16 = 0

P(2) = 2⁵ + 2⁴ - 16·2 - 16 = 32 + 16 - 32 - 16 = 0

P(-2) = (-2)⁵ + (-2)⁴ - 16·(-2) - 16 = -32 + 16 + 32 - 16 = 0

Por lo tanto, las raíces enteras del polinomio son   - 1 ,   + 2   y   - 2.

4)   x⁴ - x³ + 4x² - 256

Las raíces enteras se encuentran entre los divisores del término independiente del polinomio:   ±1 ,   ±2 ,   ±4 ,   ±8 ,   ±16 ,   ±32 ,   ±64 ,   ±128   y   ±256.

P(4) = 4⁴ - 4³ + 4·4² - 256 = 256 - 64 + 64 - 256 = 0

Por lo tanto la única raíz es 4.

Hallar un polinomio cuyas raíces sean   0 ,  1 ,  - 2   y   3

P(x) = x (x - 1) (x + 2) (x + 3) = (x² - x) (x² + 5x + 6) = x⁴ + 5x³ + 6x² - x³ - 5x² - 6x = x⁴ + 4x³ + x² - 6x

Descomponer las siguientes expresiones notables en productos de dos o más factores:

1)   x² + 2x + 1

x² + 2x + 1 = (x + 1) (x + 1)

Trinomio cuadrado perfecto de la expresión notable:   (x + y)² = x² + 2xy + y²

2)   x² - 6x + 9

x² - 6x + 9 = (x - 3) (x - 3)

Trinomio cuadrado perfecto de la expresión notable:   (x - y)² = x² - 2xy + y²

Trinomio cuadrado perfecto de la expresión notable:   (x - y)² = x² - 2xy + y²

4)   x⁴ + 16x² + 64

x⁴ + 16x² + 64 = (x²)² + 2·8x² + (8²) = (x² + 8)²

Trinomio cuadrado perfecto de la expresión notable:   (x + y)² = x² + 2xy + y²

5)   x² - 16

x² - 16 = (x + 4) (x - 4)

Diferencia de cuadrados de la expresión notable:   x² - y² = (x + y) (x - y)

6)   16x² - 9y²

16x² - 9y² = (4x)² - (3y)² = (4x + 3y) (4x - 3y)

Diferencia de cuadrados de la expresión notable:   x² - y² = (x + y) (x - y)

7)   x¹⁶ - y¹⁶

x¹⁶ - y¹⁶ = (x⁸)² - (y⁸)² = (x⁸ + y⁸)(x⁸ - y⁸)

Diferencia de cuadrados de la expresión notable:   x² - y² = (x + y) (x - y)

8)   x³ + 6x² + 12x + 8

x³ + 6x² + 12x + 8 = (x + 2)³

Expresión notable de:   (x + y)³ = x³ + 3x²y + 3xy² + y³

9)   x³ - 3x² + 3x - 1

x³ - 3x² + 3x - 1 = (x - 1)³

Expresión notable de:   (x - y)³ = x³ - 3x²y + 3xy² - y³

10)   8x³ + 1

8x³ + 1 = (2x)³ + 1³ = (2x + 1)(4x² - 2x + 1)

Expresión notable de:   x³ + y³ = (x + y) (x² - xy + y²)

11)   x³ - 27

x³ - 27 = x³ - 3³ = (x - 3)(x² + 3x + 9)

Expresión notable de:   x³ - y³ = (x - y) (x² + xy + y²)

Factoriza los siguientes trinomios:

1)   x² - x - 2

Por lo tanto se trata de un polinomio irreducible.

Al tratarse de una ecuación de segundo grado podemos resolver directamente la ecuación, aplicar la regla de Ruffini o en último lugar, aplicar el teorema del resto.

En primer lugar realizamos la factorización resolviendo la ecuación de segundo grado:

x² - x - 2 ,    donde a = 1 ,   b = -1   y   c = -2

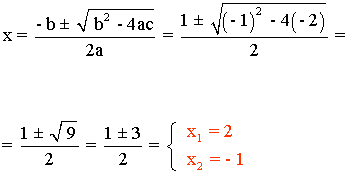
Por lo tanto, la ecuación se anula para   x₁ = 2   y para   x₂ = - 1.

El trinomio es una ecuación de segundo grado la cual se descompone de la siguiente manera:

ax² + bx + c = a (x - x₁) (x - x₂)

Es decir:   x² - x - 2 = (x - 2) (x + 1)

También podemos llegar al mismo resultado si aplicamos la regla de Ruffini:

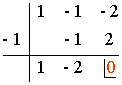
Es decir:   x² - x - 2 = (x + 1) (x - 2)

2)   42 - x - x²

Realizamos la factorización resolviendo la ecuación de segundo grado:

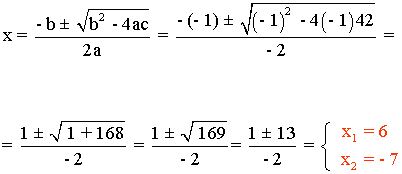
Las raíces son   x₁ = 6   y   x₂ = - 7.

El trinomio es una ecuación de segundo grado la cual se descompone de la siguiente manera:

ax² + bx + c = a (x - x₁) (x - x₂)

42 - x - x² = - (x - 6) (x + 7) = (6 - x) (x + 7)

3)   3x² + 10x + 3

Resolvemos la ecuación de segundo grado para calcular las raíces:

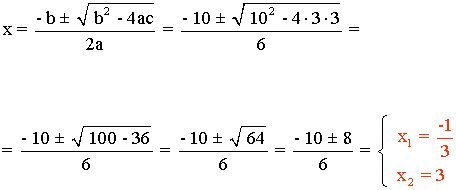
El trinomio es una ecuación de segundo grado la cual se descompone de la siguiente manera:

ax² + bx + c = a (x - x₁) (x - x₂)

Descomponer en producto de factores los siguientes polinomios:

1)   x³ - x² - x + 1

Aplicamos la regla de Ruffini para los divisores de 1, es decir,   ±1.

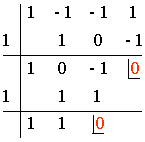
Por lo tanto:   x³ - x² - x + 1 = (x - 1) (x - 1) (x + 1) = (x - 1)² (x + 1)

2)   x³ + 2x² + 2x + 1

Aplicamos la regla de Ruffini para los divisores de 1, es decir,   ±1.

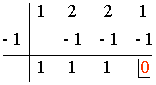
Por lo tanto:   x³ + 2x² + 2x + 1 = (x + 1) (x² + x + 1)

Si intentamos resolver la ecuación de segundo grado   x² + x + 1 = 0   ocurre lo siguiente:

Es decir, el discriminante es negativo, por lo que las raíces son imaginarias y no podemos descomponer dicho polinomio.

3)   x⁴ + 2x³ - 3x² - 4x + 4

En este caso aplicamos la regla de Ruffini para los divisores de 4.

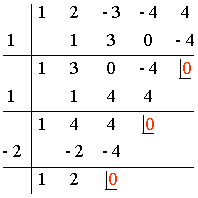
Es decir:   x⁴ + 2x³ - 3x² - 4x + 4 = (x - 1) (x - 1) (x + 2) (x + 2) = (x - 1)² (x + 2)²

4)   x⁴ - 6x³ - 11x² + 96x - 80

Volvemos a utilizar la regla de Ruffini.

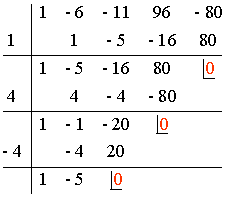
Por lo tanto:   x⁴ - 6x³ - 11x² + 96x - 80 = (x - 1) (x - 4) (x + 4) (x - 5)

5)   6x³ + 7x² - 9x + 2

Comenzamos aplicando la regla de Ruffini con los divisores del término independiente.

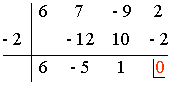
Es decir:   6x³ + 7x² - 9x + 2 = (x + 2) (6x² - 5x + 1)

Llegados a este punto no podemos continuar aplicando la regla de Ruffini ya que no es divisible entre   ±1.

A continuación buscamos las raíces del polinomio:   6x² - 5x + 1

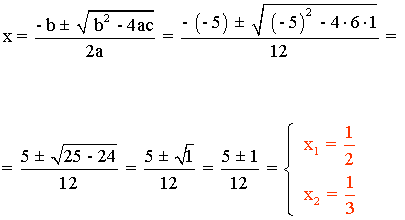
Finalmente, el polinomio inicial se descompone de la siguiente manera:

Demuestra que los siguientes polinomios son irreducibles:

1)   x² + 6

Si intentamos resolver la ecuación de segundo grado   x² + 6 = 0   obtenemos que:

Es decir, no tiene soluciones reales, por lo tanto el polinomio inicial es irreducible.

2)   3x² + 3x + 3

3x² + 3x + 3 = 3(x² + x + 1)

Si intentamos resolver la ecuación de segundo grado   x² + x + 1 = 0   ocurre lo siguiente:

Es decir, el discriminante es negativo, por lo que las raíces son imaginarias y no podemos descomponer dicho polinomio.

Este polinomio sería reducible si tuviera un factor de grado 1 o mayor. En este caso el único factor real es de grado 0.

Por lo tanto se trata de un polinomio irreducible.

3)   x⁴ + 1

Este polinomio nunca se anula puesto que   x⁴ + 1 > 0   para cualquier valor de x.

Por lo tanto no posee raíces reales y se trata de un polinomio irreducible.

4)   x² - x + 1

Al intentar resolver la ecuación de segundo grado   x² - x + 1 = 0   ocurre lo siguiente:

Por lo tanto, al igual que ocurre en el apartado 2, este polinomio es irreducible.

Halla el máximo común divisor y el mínimo común multiplo de los siguientes polinomios:

1)   P(x) = x⁴ - 5x³ + 5x² + 5x - 6   y   Q(x) = x⁶ - 4x⁵ + 3x⁴ + 4x³ - 5x² + 1

En primer lugar factorizamos el polinomio   P(x)   aplicando para ello la regla de Ruffini.

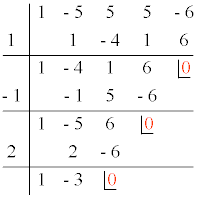
Por lo tanto, el polinomio   P(x)   se descompone de la siguiente forma:

P(x) = (x - 1) (x + 1) (x - 2) (x - 3)

A continuación descomponemos en factores el polinomio   Q(x)   aplicando también la regla de Ruffini:

En el último paso al aplicar la regla de Ruffini, el polinomio no es divisible ni por   + 1   ni por   - 1.

Por lo tanto resolvemos la ecuación de segundo grado:   x² - 2x - 1 = 0

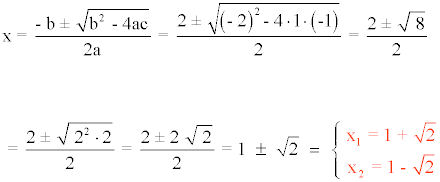
Finalmente, el polinomio   Q(x)   se descompone de la siguiente forma:

Q(x) = (x - 1)³ (x + 1) (x - 1 - √2) (x - 1 + √2)

Una vez descompuestos factorialmente ambos polinomios podemos calcular el M.C.D. y el m.c.m.:

M.C.D. son los factores comunes de menor exponente.

M.C.D. [ P(x) , Q(x) ] = (x - 1) (x + 1) = (x² - 1)

m.c.m. son los factores comunes y no comunes de mayor exponente.

m.c.m. [ P(x) , Q(x) ] = (x - 1)³ (x + 1) (x - 2) (x - 3) (x - 1 - √2) (x - 1 + √2)

2)   P(x) = x⁶ - x²   y   Q(x) = x⁴ - x³ + x² - x

El polinomio   P(x)   lo podemos descomponer sacando factor común y aplicando la igualdad notable diferencia de cuadrados igual a suma por diferencia:

P(x) = x² (x⁴ - 1) = x² [(x²)² - 1²] = x² (x² - 1) (x² + 1) = x² (x + 1) (x - 1) (x² + 1)

Donde el factor   x² + 1   es irreductible puesto que no se anula para ningún valor real de   x.

Para descomponer en factores   Q(x)   sacamos factor común y despues aplicamos la regla de Ruffini.

Q(x) = x (x³ - x² + x - 1)

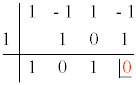
Por lo tanto, el polinomio   Q(x)   se descompone de la siguiente forma:

Q(x) = x (x - 1) (x² + 1)

Al igual que ocurriese anteriormente, el polinomio   x² + 1   es irreducible.

Una vez descompuestos factorialmente ambos polinomios, calculamos el M.C.D. y el m.c.m.:

M.C.D. [ P(x) , Q(x) ] = x (x - 1) (x² + 1)

m.c.m. [ P(x) , Q(x) ] = x² (x + 1) (x - 1) (x² + 1)

Tabla de fórmulas de factorización:

Diferencia de cuadrados	a2  -  b2  =  (a + b) (a - b)
Trinomio cuadrado perfecto: desarrollo binomio positivo al cuadrado	a2  +  2ab  +  b2  =  (a + b)2
Trinomio cuadrado perfecto: desarrollo binomio negativo al cuadrado	a2 - 2ab  +  b2  =  (a - b)2
Suma de cubos	a3  +  b3  =  (a + b) (a2  - ab + b2)
Diferencia de cubos	a3  -  b3  =  (a - b) (a2 + ab  + b2)
desarrollo binomio positivo al cubo	a3  +  3a2b  +  3ab2  +  b3  =  (a + b)3
desarrollo binomio negativo al cubo	a3  -  3a2b  +  3ab2  -  b3  =  (a - b)3