Descomposición factorial de un polinomio
Factorizar un polinomio es escribirlo como producto de polinomios del menor grado posible.
Para factorizar un polinomio se utilizan distintas técnicas.
Métodos para factorizar un polinomio
Sacar factor común.
P(x) = 3x3 + 5x2 - x = x (3x2 + 5x - 1)
Aplicar las fórmulas de factorización importantes.
| Diferencia de cuadrados | a2 - b2 = (a + b) (a - b) |
|---|---|
| Trinomio cuadrado perfecto | a2 + 2ab + b2 = (a + b)2 |
| Trinomio cuadrado perfecto | a2 - 2ab + b2 = (a + b)2 |
| Suma de cubos | a3 + b3 = (a + b) (a2 - ab + b2) |
| Diferencia de cubos | a3 - b3 = (a - b) (a2 + ab + b2) |
| Desarrollo de suma de binomio al cubo | a3 + 3a2b + 3ab2 + b3 = (a + b)3 |
| Desarrollo de la diferencia de un binomio al cubo | a3 - 3a2b + 3ab2 - b3 = (a - b)3 |
P(x) = 9x2 + 12x + 4 = (3x + 2)2
P(x) = 8x3 - 12x2 + 3x - 1 = (2x - 1)3
Calcular las raices del polinomio y realiza su descomposición factorial
P(x) = x4 - 10x2 + 9
No es posible sacar factor común ni es posible aplicar igualdades notables.
Se buscan sus raices enteras entre los divisores del término independiente. Para ello utilizamos reiteradamente la regla de Ruffini.
Div(9) = {1, -1, 3, -3, 9, -9}
Probamos sucesivamente cuales son raices entre todos los divisores de 9. Empezamos con x = 9
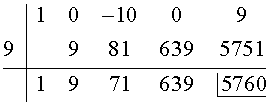
Observamos que x = 9 no es raiz de P(x).
Probamos ahora con x = 1.
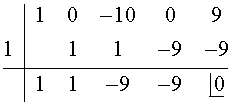
P(x) = (x - 1) (x3 + x2 - 9x - 9)
A continuación buscamos las raices del polinomio cociente: x3 + x2 - 9x - 9
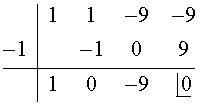
P(x) = (x - 1) (x + 1) (x2 - 9)
Cuando obtenemos un polinomio cociente de grado 2, podemos resolver la ecuación de segundo grado: x2 - 9 = 0
Otra opción es continuar calculando las raices mediante el método de Ruffini.
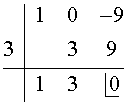
P(x) = (x - 1) (x + 1) (x - 3) (x + 3)
Por lo tanto las raices del polinomio son x = 1, x = -1, x = 3 y x = -3


 INICIO
INICIO

