Lenguaje algebraico
1. Sea x un número cualquiera. Escribir las siguientes expresiones mediante lenguaje algebraico.
| Expresión escrita | Expresión algebraica |
|---|---|
| El doble de x | 2x |
| El triple de x | 3x |
| El cuádruple de x | 4x |
| La mitad de x | 1/2 x |
| Un tercio de x | 1/3 x |
| Los tres cuartos de x | 3/4 x |
| El 80% de x | (80/100)·x = 0,8x |
| El 25% de x | (25/100)·x = 0,25x |
| El consecutivo o el sucesor de x (x∈Ζ) | x + 1 |
| El anterior o antecesor de x (x∈Ζ) | x - 1 |
| Tres números consecutivos cualesquiera | x , (x + 1) , (x + 2) , o bien, (x - 1) , x , ( x + 1) |
| Los siguientes tres números consecutivos de x | (x + 1) , ( x + 2) , (x + 3) |
| Tres números pares consecutivos | 2x , 2(x + 1) , 2(x + 2) , es decir: 2x , (2x + 2) , (2x + 4) |
| Tres números impares consecutivos | 2x+1 , (2x + 2) + 1 , (2x + 4)+1 , es decir: (2x + 1) , (2x + 3) , (2x + 5) |
| El resultado de sumar un número a 5 | 5 + x |
| La suma de algún número y 11 | x + 11 |
| El resultado de restar a 9 algún número | 9 - x |
| 7 por algún número | 7x |
| Dos veces la suma de un número más 4 | 2 (x + 4) |
| Un número y su raíz cuadrada | x , √x |
| Dos números, uno el triple del otro | x , 3x |
| Dos números cuya razón es 2/3 | 2x/3x = 2/3 ⇒ 2x , 3x |
| Tres números proporcionales a 2 , 3 y 4 | 2x , 3x , 4x |
| Tres números inversamente proporcionales a 2 , 3 y 4 | x/2 , x/3 , x/4 |
2. Escribe las siguientes ecuaciones con una incógnita.
| Expresión escrita | Expresión algebraica |
|---|---|
| La suma de tres números consecutivos es 20 | x + (x + 1) + (x + 2) = 20 |
| La suma de dos números impares consecutivos es 18 | (2x + 1) + (2x + 3) = 18 |
| La suma de dos números pares consecutivos es 26 | 2x + (2x + 2) + (2x + 4) = 26 |
| Un número más su séptima parte es 18 | x + x/7 = 18 |
| La suma de dos números consecutivos es 16 | x + (x + 1) = 16 |
| La suma de tres números consecutivos es 20 | x + (x + 1) + (x + 2) = 20 |
| La suma de cuatro números consecutivos es 42 | x + (x + 1) + (x + 2) + (x + 3) = 20 |
| La suma de dos números impares consecutivos es 18 | (2x + 1) + (2x + 3) = 18 |
| La suma de tres números pares consecutivos es 26 | 2x + (2x + 2) + (2x + 4) = 26 |
| La suma de tres múltiplos de 3 consecutivos es 84 | 3x + 3(x + 1) + 3(x + 2) = 84 |
| La suma de tres múltiplos de 5 consecutivos es 115 | 5x + 5(x + 1) + 5(x + 2) = 115 |
| La suma de cuatro números proporcionales a 2 , 3 , 4 y 5 es 54 | 2x + 3x + 4x + 5x = 54 |
| La suma de cuatro números inversamente proporcionales
a 2 , 3 , 4 y 5 es 345 |
x/2 + x/3 + x/4 + x/5 = 345 |
1. Sea x un número cualquiera. Escribir las siguientes expresiones mediante lenguaje algebraico.
| Expresión escrita | Expresión algebraica |
|---|---|
| El cuadrado de x | x2 |
| El cubo de x | x3 |
| Un número y su cuadrado | x , x2 |
| Un número y su raíz cuadrada | x2 , x |
| Los cuadrados de tres números consecutivos | x2 , (x + 1)2 , (x + 2)2 |
| Los cuadrados de dos números cuya suma es 6 | x2 , (6 - x)2 x + (6 - x) = 6 |
| Los cuadrados de dos números cuya diferencia es 12 | x2 , (x - 12)2 x - (x - 12) = 12 |
| Los cuadrados de dos números cuyo cociente es 9 | x2 , (9x)2 9x/x = 9 |
| Los cuadrados de tres números proporcionales a 4, 5 y 6 | (4x)2, (5x)2, (6x)2 4x , 5x , 6x |
2. Escribe las siguientes ecuaciones con una incógnita.
| Expresión escrita | Expresión algebraica |
|---|---|
| La suma de los cuadrados de dos números consecutivos es 265 | x2 + (x + 1)2 = 265 |
| La diferencia entre los cuadrados de dos números consecutivos es 17 | (x + 1)2 - x2 = 17 |
| El producto de un número por su cuarta parte es 100 | 4x · x = 100 |
| El producto de tres números consecutivos es 120 | x · (x + 1) · (x + 2) = 120 |
| El producto de dos números impares consecutivos es 143 | (2x + 1)(2x + 3) = 143 |
1. Escribir las siguientes expresiones mediante lenguaje algebraico.
| Expresión escrita | Expresión algebraica |
|---|---|
| Dos números | x , y |
| Tres números | x , y , z |
| Un número de dos cifras | xy 10x + y |
| Un número de tres cifras | xyz 100x + 10y + z |
| Un número de cuatro cifras | xyzt 1000x + 100y + 10z + t |
2. Escribe las siguientes ecuaciones con dos incógnitas.
| Expresión escrita | Expresión algebraica |
|---|---|
| La suma de dos números es 15 | x + y = 15 |
| La diferencia de dos números es 8 | x - y = 8 |
| La razón de dos números es 15 | x/y = 15 |
| El producto de dos números es 21 | x · y = 16 |
| La diferencia de los cuadrados de dos números es 16 | x2 - y2 = 16 |
| La suma de los cuadrados de dos números es 41 | x2 + y2 = 41 |
| El cuadrado de la diferencia entre dos números es 25 | (x - y)2 = 25 |
| El cuadrado de la suma de dos números es 225 | (x + y)2 = 225 |
| Un número excede a otro en 12 | x = y + 12 |
| El doble de la suma de dos números es 34 | 2(x + y) = 34 |
Completa una tabla atendiendo a los siguientes enunciados:
1) Sonia tiene x años.
2) Su esposo, Antonio, tiene 2 años más.
3) Paco, su padre, le dobla la edad.
4) Su madre, María, tiene 4 años menos que su marido.
5) Sonia tiene dos hijos gemelos, Pedro y Ana, y los tuvo con 25 años.
6) Su hija menor, Alicia, tiene la mitad de años que los gemelos.
7) La edad del abuelo de Sonia, David, es la de ésta y su marido juntos.
| Edad | |
|---|---|
| Sonia | x |
| Antonio | x + 2 |
| Paco | 2x |
| María | 2x - 4 |
| Pedro y Ana | x - 25 |
| Alicia | (x - 25)/2 |
| David | x + (x + 2) = 2x + 2 |
Expresa algebraicamente el perímetro y el área de los siguientes rectángulos:
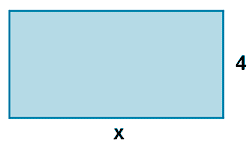
Perímetro: 2 · x + 2 · 4 = 2x + 8
Área: 4x
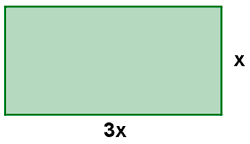
Perímetro: 2 · x + 2· 3x = 2x + 6x = 8x
Área: x · 3x = 3x2
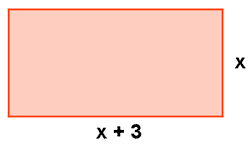
Perímetro: 2 · x + 2 · (x + 3) = 2x + 2x + 6 = 4x + 6
Área: x · (x + 3) = x2 + 3x
Expresa algebraicamente el perímetro y el área de los siguientes rectángulos:
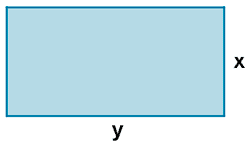
Perímetro: 2 · x + 2 · y = 2x + 2y
Área: xy
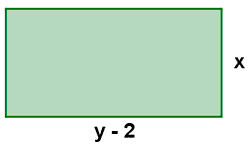
Perímetro: 2 · x + 2 · (y - 2) = 2x + 2y - 4
Área: x · (y - 2) = xy - 2x
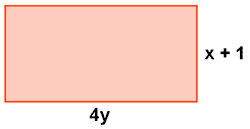
Perímetro: 2 · (x + 1) + 2 · 4y = 2x + 2 + 8y
Área: (x + 1) · 4y = 4yx + 4y
Ejemplos de problemas con ecuaciones de primer grado
1) Hallar 6 números consecutivos cuya suma sea 597
1. Observamos que:
Dos números consecutivos se diferencian en una unidad.
Como queremos hallar seis, llamaremos al primero de ellos 'x'.
Además de ser consecutivos, tienen que sumar 597.
2. Escribimos la ecuación:
Si x es el primer número, los siguientes cinco números consecutivos, serán:
x , x + 1 , x + 2 , x + 3 , x + 4 , x + 5
Los seis números tienen que sumar 597, luego:
x + (x + 1) + (x + 2) + (x + 3) + (x + 4) + (x + 5) = 597
3. Resolvemos la ecuación:
x + (x + 1) + (x + 2) + (x + 3) + (x + 4) + (x + 5) = 597 ⇔ 6x + 15 = 597 ⇔ 6x = 582 ⇔ x = 97
4. Resolvemos el problema:
El primer número es x = 97 , por tanto, los siguientes 5 números serán: 98 , 99 , 100 , 101 , 102
Los números pedidos son: 97 , 98 , 99 , 100 , 101 , 102
2) Pedro tiene 42 años y su hijo 10 años. ¿Dentro de cuántos años la edad del padre será triple que la del hijo?
1. Observamos que:
La incógnita es el número de años que tienen que pasar para que se cumpla que "la edad del padre será triple que la del hijo". Llamaremos a dicho número de años 'x'.
2. Escribimos la ecuación:
Actualmente, Pedro tiene 42 y su hijo 10 años. Si pasan x años, sus edades serán: 42 + x y 10 + x respectivamente.
Pasados x años, queremos que la edad del padre (42 + x) sea el triple de la de su hijo (10 + x), por tanto:
42 + x = 3 (x + 10)
3. Resolvemos la ecuación:
42 + x = 3 (x + 10) ⇔ 42 + x = 3x + 30 ⇔ 12 = 2x ⇔ x = 6
4. Resolvemos el problema:
Tienen que pasar 6 años para que Pedro tenga el triple de edad que su hijo.
3) El perímetro de un triángulo isósceles es 180 cm. Cada uno de los lados iguales es 30 cm mayor que la base. ¿Cuánto vale cada lado?
1. Después de varias lecturas observamos que:
Un triángulo isósceles es aquel que tiene dos de sus lados iguales.
El perímetro de un polígono cualquiera es la suma de sus lados. En este caso es 180 cm.
Los lados que son iguales miden 30 cm más que la base, así que, como no sabemos lo que vale dicha base la llamaremos 'x'.
2. Escribimos la ecuación:
Si la base del triángulo vale x , los lados que son iguales medirán 30 cm más, es decir: x + 30
La suma de los tres lados tiene que ser 180 cm, por tanto:
x + (x + 3) + (x + 3) = 180
3. Resolvemos la ecuación:
x + (x + 30) + (x + 30) = 180 ⇔ 3x + 60 = 180 ⇔ 3x = 120 ⇔ x = 40
4. Resolvemos el problema:
Como la base mide 40 cm, los lados que son iguales medirán: x + 30 = 40 + 30 = 70 cm
Los lados del triángulo isósceles son 40 cm , 70 cm. y 70 cm.
4) Juan tarda 6 días en hacer una obra. Paco es capaz de acabarla en 3 días. ¿En cuánto tiempo pueden hacer la obra trabajando juntos?
1. Observamos que:
Nos piden el tiempo que tardarán en hacer la obra juntos, así que llamaremos a dicho tiempo 'x'.
2. Escribimos la ecuación:
Juan tarda 6 días en hacer la obra completa, por tanto, en 1 día tendrá hecho 1/6 de la obra, y en x días, tendrá hecho: ![]()
Paco tarda 3 días en terminarla, luego en 1 día hará 1/3 de la obra, y en x días, tendrá hecho: ![]()
Si Juan hace x/6 y y Paco hace x/3 , entre los dos harán la obra completa, es decir, la unidad:
![]()
3. Resolvemos la ecuación:
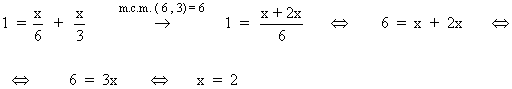
4. Resolvemos el problema:
Entre los dos tardan 2 días completos.
5) Un grifo A llena una piscina en 8 horas, otro B la llena en 10 horas. Hallar el tiempo que tardarán en llenarla los dos juntos.
1. Observamos que:
Nos piden el tiempo que tardará en llenarse la piscina, así que llamaremos a dicho tiempo 'x'.
2. Escribimos la ecuación:
Si el grifo A tarda en llenarla 8 horas, en una hora llenará: 1/8
Si el grifo B tarda en llenarla 10 horas, en una hora llenará: 1/10
Si x es el número de horas que tarda en llenarse la piscina, en una hora se habrá llenado: 1/x
En una hora tienen que llenar entre los dos 1/x , por lo que:
![]()
3. Resolvemos la ecuación:
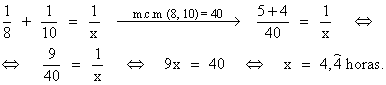
4. Resolvemos el problema:

Ejemplos de problemas con ecuaciones de segundo grado
1) Hallar dos números pares consecutivos tales que la suma de sus cuadrados sea 452.
1. Observamos que:
Queremos hallar dos números, uno será aquel número par que sea consecutivo del otro, así que llamaremos al primero 'x'.
2. Escribimos la ecuación:
Si tenemos x , su consecutivo será: x + 1
Queremos que sean pares, es decir, tienen que ser múltiplos de dos. Entonces: 2x , 2(x + 1) = 2x + 2
Sus cuadrados: (2x)2 , (2x + 2)2
La suma de ambos tiene que ser 452:
(2x)2 + (2x + 2)2 = 452
3. Resolvemos la ecuación:
(2x)2 + (2x + 2)2 = 452 ⇔ 4x2 + 4x2 + 8x + 4 = 452 ⇔ 8x2 + 8x + 4 = 452 ⇔ 8x2 + 8x - 448 = 0
Simplificamos la ecuación dividiendo entre 8: x2 + x - 56 = 0
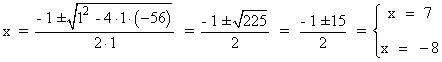
4. Resolvemos el problema:
Si x = 7 ⇒ 2x = 14 y 2x + 2 = 16
Si x = - 8 ⇒ 2x = - 16 y 2x + 2 = - 14
El problema tiene dos soluciones posibles: 14 y 16 , - 16 y -14
2) Los tres lados de un triángulo miden 18, 16 y 9 cm. Determinar qué misma cantidad se debe restar a cada lado para que resulte un triángulo rectángulo.
1. Observamos que:
Un triángulo rectángulo es aquel que tiene un ángulo de 90º.
Tenemos que restar la misma cantidad a cada lado, por lo que llamaremos a dicha cantidad 'x'.
2. Escribimos la ecuación:
Tenemos que restar a cada lado la misma cantidad, por lo que los lados del nuevo triángulo serán: 18 - x , 16 - x , 9 - x
El nuevo triángulo tiene que ser rectángulo, por lo que tiene que cumplir el teorema de pitágoras:
(18 - x)2 = (16 - x)2 + (9 - x)2
3. Resolvemos la ecuación:
(18 - x)2 = (16 - x)2 + (9 - x)2 ⇔ 324 - 36x + x2 = 256 - 32x + x2 + 81 - 18x + x2 ⇔ x2 - 14x + 13 = 0
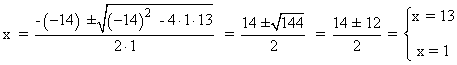
4. Resolvemos el problema:
La solución x = 13 no es válida, ya que entonces tendríamos el lado: 9 - x = 9 - 13 = - 4 < 0 y no podemos dar dimensiones negativas.
Por tanto, nos quedamos con la solución x = 1 y los lados miden: 17 , 15 y 8.
Ejemplos de problemas con sistemas de ecuaciones
1) La suma de dos números es 10 y la de sus cuadrados 68. ¿Cuáles son estos números?
1. Observamos que:
Queremos hallar dos números distintos, así que los llamaremos 'x' e 'y'.
2. Escribimos la ecuación:
La suma de ambos tiene que dar 10: x + y = 10
Los cuadrados de dichos números son: x2 , y2
La suma de sus cuadrados es 68: x2 + y2 = 68
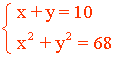
3. Resolvemos el sistema:
Despejamos la variable x en la primera ecuación: x + y = 10 ⇔ x = 10 - y
Sustituimos en la segunda ecuación:
x2 + y2 = 68 ⇒ (10 - y)2 + y2 = 68 ⇒ 100 - 20y + y2 + y2 = 68 ⇒ 2y2 - 20y + 32 = 0
Simpificamos la ecuación dividiendo entre 2: y2 - 10y + 16 = 0
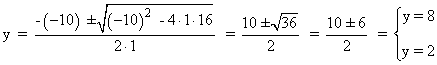
Si y = 8 ⇒ x = 10 - y = 10 - 8 = 2
Si y = 2 ⇒ x = 10 - y = 10 - 2 = 8
3. Resolvemos el problema:
Los números pedidos son 2 y 8 .
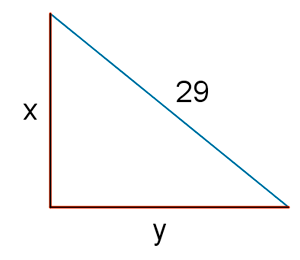
2) El perímetro de un triángulo rectángulo es de 70 cm y la hipotenusa 29 cm. Hallar los lados.
1. Observamos que:
El perímetro de un polígono cualquiera es la suma de sus lados.
Como nos dan la hipotenusa (29), tenemos que hallar cuánto miden sus dos catetos. Los llamaremos 'x' e 'y'.
2. Escribimos la ecuación:
La suma de sus lados es 70, como su hipotenusa vale 29: 29 + x + y = 70 ⇔ x + y = 70 - 29 = 41
Como es un triángulo rectángulo podemos aplicar el teorema de Pitágoras: 292 = x2 + y2 ⇔ 841 = x2 + y2
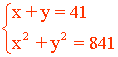
3. Resolvemos el sistema:
Despejamos la variable x en la primera ecuación: x + y = 41 ⇔ x = 41 - y
Sustituimos en la segunda:
x2 + y2 = 841 ⇒ (41 - y)2 + y2 = 841 ⇒ 1681 - 82y + y2 + y2 = 841 ⇒ 2y2 - 82y + 840 = 0
Simplificamos la ecuación dividiéndola entre 2: y2 - 41y + 420 = 0
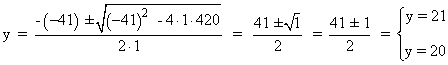
Si y = 21 ⇒ x = 41 - y = 41 - 21 = 20
Si y = 20 ⇒ x = 41 - y = 41 - 20 = 21
4. Resolvemos el problema:
Los catetos miden 21 y 20 cm.


 INICIO
INICIO