Problemas resueltos de grifos
- 1. Planteamiento general
- 2. Depósito sin desagüe I
- 3. Depósito sin desagüe II
- 4. Depósito con desagüe
Planteamiento general de un problema sobre grifos:
Supongamos que tenemos 2 grifos y un depósito a llenar.
• En una hora, el primer grifo llena 1/t1 del depósito.
• En una hora, el segundo grifo llena 1/t2 del depósito.
Si el depósito tiene un desagüe:
• En una hora, el desagüe vacía 1/t3 del depósito.
En una hora, los dos grifos juntos habrán llenado 1/T:
• Sin desagüe:
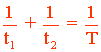
• Con desagüe:
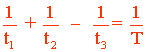
Una fuente llena un depósito en 12 h y otra lo llena en 20 h. ¿Qué tardarían en llenarlo manando juntas ambas fuentes?
Sea x el tiempo que tarda en llenarse el depósito (T = x). Entonces, en una hora se deberá llenar 1/x del depósito.
La primera fuente tarda en llenarlo t1 = 12 horas, luego en una hora habrá llenado 1/t1 = 1/12 del depósito.
La segunda fuente tarda en llenarlo t2 = 20 horas, luego en una hora habrá llenado 1/t2 = 1/20 del depósito.
Si las dos fuentes manan a la vez, deberemos tener:
![]()
Resolvemos la ecuación:
![]()
![]()
Pasamos 0,5 h a minutos: 0,5 · 60 = 30 min
Tardaría en llenarse: 7 h 30 min
Dos fuentes manando juntas tardan en llenar un depósito 2 horas y 24 minutos. Halla el tiempo que emplearía cada una de ellas sabiendo que la segunda emplea dos horas menos que la primera.
Tenemos que pasar 2 h 24 min a minutos:
2 h ⇒ 2 · 60 = 120 min
Si las dos fuentes manan a la vez, el depósito se llenará en: 120 + 24 = 144 minutos
Por tanto, en una hora se habrá llenado 1/144 del depósito
Sea x el tiempo que tarda la primera fuente en llenar el depósito. En una hora habrá llenado 1/x del depósito.
Como la segunda tarda dos horas menos (120 min) que la primera: x - 120
Y en una hora ésta habrá llenado: 1/(x - 120)
Si las dos fuentes manan a la vez, tenemos que:
![]()
Aplicamos: m.c.m.(x, x - 120, 144) = 144x(x - 120)
144(x - 120) + 144x = x(x - 120) ⇔ 144x - 17280 + 144x = x2 - 120x ⇔ x2 - 408x + 17280 = 0
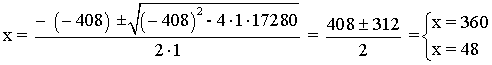
Si tomamos x = 48 como el tiempo que tarda la primera fuente, entonces la segunda tardaría: x - 120 = 48 - 120 = - 72 min ¡el tiempo no puede ser negativo!
Por tanto, la primera fuente tarda:
360 / 60 = 6 horas
Y entonces la segunda tarda:
x - 120 = 360 - 120 = 240 min
240 / 60 = 4 horas
Un depósito tiene un grifo que lo llena en 3 horas; otro tarda en llenarlo 4 horas y un desagüe lo vacía en 5 horas. ¿Cuánto tardará en llenarse si se abren a la vez los tres caños?
Sea x el tiempo que tarda en llenarse el depósito (T = x). Entonces, en una hora se deberá llenar 1/x del depósito.
El primer grifo tarda t1 = 3 horas en llenar el déposito. Por tanto, en una hora llenará 1/t1 = 1/3 del depósito.
El segundo grifo tarda t2 = 5 horas en llenar el déposito. Luego, en una hora llenará 1/t2 = 1/5 del depósito.
El desagüe tarda t3 = 5 horas en vaciar el depósito. Así que en una hora vaciará 1/t3 = 1/5 del depósito.
Por tanto:
![]()
Resolvemos la ecuación:
![]()
![]()
Pasamos 0,60869 h a minutos: 0,60869 · 60 = 36,5214 ≈ 36 min
Tardaría en llenarse: 2 h 36 min


 INICIO
INICIO