Problemas resueltos sobre números II
1. ¿Qué número natural se diferencia de sus cuadrado en 42 unidades?
Llamaremos a dicho número natural 'x'.
El cuadrado de x es: x2
La diferencia entre x y su cuadrado tiene que dar 42, por tanto:
![]()
Resolemos la ecuación de segundo grado:
![]()
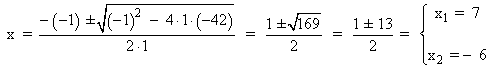
El problema nos pide que sea un número natural, por tanto, la única solución válida es: x = 7
2. Hallar un número que quitándole 60 unidades a su cuadrado resulte lo mismo que quitándole 4 unidades al propio número.
Sea 'x' dicho número.
Si le quitamos 60 unidades a su cuadrado tenemos: x2 - 60
Y si le quitamos 4 unidades a dicho número: x - 4
El problema dice que ambos resultados son iguales, luego:
![]()
Resolvemos la ecuación:
x2 - 60 = x - 4 ⇔ x2 - x - 56 = 0
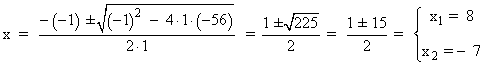
Ambas soluciones cumplen las condiciones del problema, por lo que los números pedidos son: 8 y - 7
1. El dividendo y el resto de una división de números naturales son 200 y 5, respectivamente. Halla el divisor y el cociente si se diferencian en dos unidades.
De forma general, podemos escribir algebraicamente una división de la siguiente forma:

Tenemos que hallar el divisor y el cociente. Como se diferencian en 2 unidades, llamaremos a uno cualquiera de ellos 'x', por ejemplo, al divisor.
Por tanto, el cociente será: x - 2
Entonces, según la expresión algebraica de la división ( D = d·c + r), tenemos la ecuación:
![]()
Resolvemos la ecuación resultante:
200 = x · (x - 2) + 5 ⇔ 200 = x2 - 2x + 5 ⇔ x2 - 2x - 195 = 0
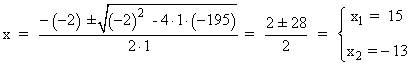
La solución x2 no es válida por ser negativa.
Por tanto, si el divisor es x = 15 , entonces el cociente es x - 2 = 13.
2. El dividendo de una división es 1081. El cociente y el resto son iguales y el divisor es doble del cociente. Halla el divisor.
Puesto que son iguales, llamaremos 'x' tanto al cociente como al resto.
Por otro lado, el divisor es el doble del cociente, es decir: 2x
Escribimos de forma algebraica la división planteada:
![]()
![]()
![]()
La ecuación a resolver es:
2x2 + x - 1081 = 0
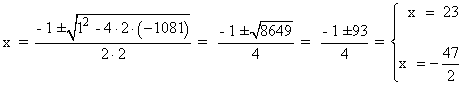
Tenemos dos soluciones posibles, como el divisor es 2x: 46 , - 47
1. Hallar tres números naturales consecutivos, tales que su producto sea igual a 8 veces su suma.
Sean x - 1 , x , x + 1 los tres números naturales consecutivos.
El problema nos dice que el producto de dichos números es igual a su suma multiplicada por 8, luego:
![]()
La resolvemos:
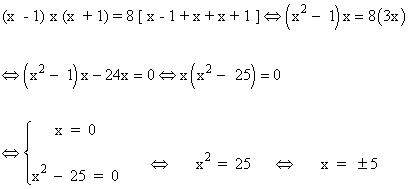
Los tres números tienen que ser naturales, por lo que la única solución válida es x = 5.
Los números que piden son: 4 , 5 y 6.
2. Si al producto de tres números consecutivos se le agrega el que no es mayor ni el menor de dichos números, se obtiene 8000. ¿Cuál es la suma de los números?
Sea 'x' el número mediano, el menor consecutivo será x - 1 y el mayor consecutivo será x + 1
El que no es mayor ni menor de los tres es x , por tanto, si lo agregamos al producto de los tres nos queda la siguiente ecuación:
![]()
La resolvemos:

Si x = 20 , entonces: x - 1 = 19 y x + 1 = 21
Nos piden la suma de dichos números: (x - 1) + x + (x + 1) = 19 + 20 + 21 = 60
¿Qué número aumentado 6 veces su raíz cuadrada da 135?
Consideremos 'x2' dicho número, así, su raíz cuadrada será 'x'.
Tenemos que aumentar x2 en 6 veces su raíz, es decir: x2 + 6x
Según el enunciado, el resultado debe dar 135, por tanto se nos plantea la siguiente ecuación:
![]()
La resolvemos:
x2 + 6x = 135 ⇔ x2 + 6x - 135 = 0
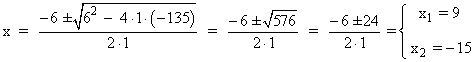
El resultado x = -15 no es una solución válida para el problema, ya que en ese caso tendríamos x2 = 225 y su ráiz cuadrada es 15 ≠ - 15.
El problema tiene una única solución: x = 9 , x2 = 81
1. Hallar dos números sabiendo que su producto es igual a su suma y a cinco veces su diferencia.
Queremos hallar dos números distintos, así que los llamaremos 'x' e 'y'.
El producto de ambos es igual a su suma: x · y = x + y
Su producto (o su suma) es 5 veces la diferencia entre ambos: x + y = 5(x - y)
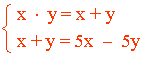
Resolvemos el sistema mediante sustitución:
Despejamos la variable y de la segunda ecuación:
![]()
Sustituimos en la primera ecuación y resolvemos:
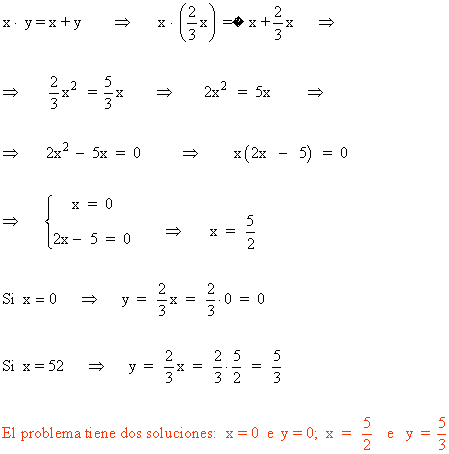
2. Halla dos números positivos cuyo producto sea 1200 y su cociente 1/3
Queremos hallar dos números distintos, así que los llamaremos 'x' e 'y'.
Su producto es 1200: x · y = 1200
Su cociente es 1/3: ![]()
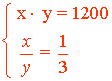
Despejamos la variable y de la segunda ecuación:
![]()
Sustituimos en la primera ecuación y resolvemos:

1. Halla dos números naturales sabiendo que sumando 7 veces el primero a 8 veces el segundo tenemos 264, y restando amos, 27.
Queremos hallar dos números distintos, así que los llamaremos 'x' e 'y'.
Sabemos que 264 es la suma de 7 veces el primero más 8 veces el segundo, por tanto: 7x + 8y
Por otro lado, la diferencia entre ambos vale 27: x - y = 27
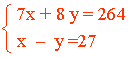
Resolvemos el sistema mediante el método de reducción:
Multiplicamos por 8 la segunda ecuación.
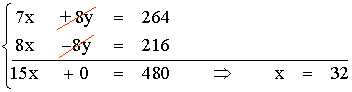
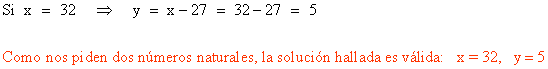
2. La suma de dos números es 7, y la de sus inversos 7/12. Hallar el valor de estos dos números.

Reuniendo las dos ecuaciones tenemos el sistema:
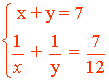
Resolvemos el sistema mediante el método de sustitución:


 INICIO
INICIO