Problemas resueltos de aleaciones

Planteamiento general de un problema sobre aleaciones:

La ley de la aleación es la relación entre el peso del metal fino (más valioso) y el peso total. Siendo la ley igual a 1 cuando el metal es puro.

Supongamos que queremos hacer una aleación con dos metales, A y B, cada uno con una ley de aleación distinta.

      •   C_A    es la cantidad del metal A:               C_A = x

      •   C_B    es la cantidad del metal B:               C_B = C_a - x

      •   C_a    es la cantidad total de la aleación:     C_a = C_A + C_B

      •   L_A    es la ley de aleación del metal  A.

      •   L_B    es la ley de aleación del metal  B.

      •   L_a    es la ley de aleación del metal resultante.

Tenemos la siguiente fórmula general:

                        C_A · L_A  +  C_B· L_B  =  C_a · L_a

También podemos poner los datos en una tabla:

	Cantidad	Ley	Metal
Metal A	CA	LA	CA · LA
Metal B	CB	LB	CB · LB
Aleación	CA + CB	La	(CA + CB) · La

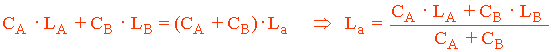
Un lingote de plata de 300 g de ley del 91 % (91 % de pureza) se funde con otro de 200 g de 82 % de ley. ¿Cuál es la ley del nuevo lingote?

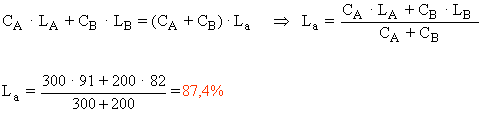
Un joyero quiere construir una joya de plata de 40 g. de peso y de ley 0,900. Para ello dispone de dos lingotes de este metal con leyes 0,975 y 0,850. ¿Qué cantidad tiene que tomar de cada uno de estos lingotes para hacer la joya indicada?

Rellenamos la tabla con los datos que nos da el problema:

	Cantidad	Ley	Metal
Plata A	x	0,975	0,975x
Plata B	40 - x	0,850	(40 - x) · 0,850
Aleación	40	0,900	40 · 0,900

La cantidad total de aleación (40 g) es la suma de ambos metales. Por tanto, si tenemos  x  gramos de plata de tipo A, la cantidad de plata de tipo B será:     40 - x

Aplicando la fórmula general a los datos que tenemos:

0,975x  +  (40 - x) · 0,850  =  40 · 0,900

Resolvemos la ecuación de primer grado:

            0,975x  +  (40 - x) · 0,850  =  40 · 0,900     ⇔     0,975x + 34 - 0,850x = 36     ⇔     0,125x = 2     ⇔     x = 16 g.

            Si  x = 16     ⇒     40 - x = 24 g.

El joyero tendrá que tomar  16 g.  de plata de ley 0,975 y   24 g.   de plata de ley 0,850.

Un orfebre tiene dos lingotes. El primero contiene 540 g. de oro y 60 g. de cobre. El segundo 400 g. de oro y 100 g. de cobre. ¿Qué cantidad deberá tomar de cada uno de ellos para formar otro lingote que pese 640 g. y cuya ley sea 0,825?

En primer lugar, calculamos las leyes de aleación de cada lingote. Para ello, tenemos que tener en cuenta que el oro es más valioso que el cobre.

            Lingote A:

                        

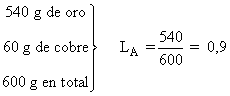
            Lingote B:

                        

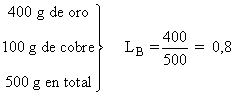
En segundo lugar, rellenamos la tabla con los datos que nos da el problema:

	Cantidad	Ley	Metal
Lingote A	x	0,9	0,9x
Lingote B	640 - x	0,8	(640 - x) · 0,8
Aleación	640	0,825	640 · 0,825

La cantidad total de aleación (640 g) es la suma de ambos metales. Por tanto, si tenemos  x  gramos del lingote A, la cantidad de gramos que tomemos del lingote B será:     640 - x

Aplicando la fórmula general a los datos que tenemos:

0,9x  +  (640 - x) · 0,8  =  640 · 0,825

Resolvemos la ecuación de primer grado:

            0,9x  +  (640 - x) · 0,8  =  640 · 0,825     ⇔     0,9x + 512 - 0,8x = 528     ⇔     0,1x = 16     ⇔     x = 160 g

            Si   x = 160     ⇒     640 - x = 420 g

El orfebre tendrá que tomar  160 gramos  del primer lingote y  420 gramos  del segundo.