Problemas geométricos resueltos
- 1. Fórmulas I
- 2. II
- 3. Ángulos
- 4. Triángulo
- 5. Cuadrado
- 6. Rectángulo
- 7. Trapecio
- 8. Rombo
- 9. Cubo
- 10. Ortoedro
- 11. Prisma
Figuras planas
| Nombre | Dibujo | Perímetro | Área |
|---|---|---|---|
| Cuadrado |  |
P = 4a | A = a2 |
| Rectángulo |  |
P = 2b + 2a | A = ba |
| Rombo | 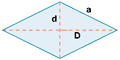 |
P = 4a | |
| Romboide | 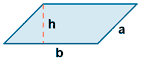 |
P = 2a + 2b | A = b h |
| Trapecio | 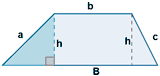 |
P = a + B + b + c | |
| Trapecio isósceles |
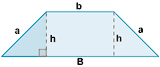 |
P = 2a + B + b | |
| Triángulo | 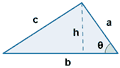 |
P = a + b + c |
|
| Triángulo equilátero |
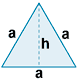 |
P = 3a |
|
| Triángulo rectángulo |
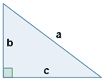 |
P = a + b + c a2 = b2 + c2 |
|
| Hexágono regular |
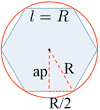 |
P = 6l = 6R ap = apotema |
|
| Pentágono regular |
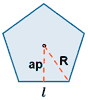 |
P = 5l | ap = apotema |
| Círculo | 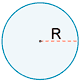 |
L = 2πR | A = πR2 |
| Sector circular |
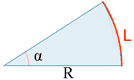 |
L = R α P = 2R + L |
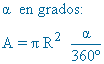 |
| Corona circular |
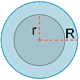 |
L = 2π (R + r) | A = π (R - r) |
| Elipse | 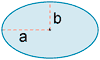 |
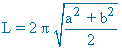 |
A = π a b |
Cuerpos en el espacio
| Dibujo | Área | Volumen | |
|---|---|---|---|
| Cubo | 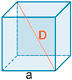 |
A = 6 a2 |
V = a3 |
| Ortoedro | 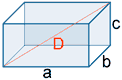 |
A = 2( a·b + a·c + b·c ) |
V = a · b · c |
| Prisma | 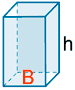 |
PB = perímetro de la base AL = PB · h AT = AL + 2·AB |
V = AB h |
| Pirámide | 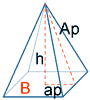 |
PB = perímetro base Ap = apotema pirámide ap = apotema de la base Ap2 = h2 + ap2 AT = AL + AB |
|
| Cilindro | 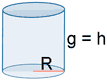 |
AL = 2 π R h AB =2 π R2 AT = 2 π R (h + R) |
V = π R2 h |
| Cono | 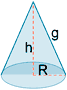 |
g2 = R2 + h2 AL = π R g AB = π R2 AT = π R (g + R) |
|
| Tronco de cono |
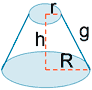 |
AL = π (R + r) g AT = π [ g(R + r) + R2 + r2 ] |
|
| Esfera | 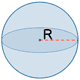 |
A = 4 π R2 | |
| Cuña | 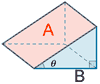 |
A = área cara superior AB = área base A = AB sec θ |
¿Cuánto mide un ángulo si su complementario es el doble más 15º?
Dos ángulos son complementarios si suman 90º.
Sea x uno de dicho ángulos.
El ángulo complementario de x mide el doble de x más 15º, luego medirá: 2x + 15º
La suma de ambos ángulos mide 90º, es decir:
Ángulo + Complementario = 90º
x + (2x + 15º) = 90º
Resolvemos la ecuación de primer grado:
x (2x + 15º) = 90 ⇔ 3x + 15º = 90º ⇔ 3x = 75º ⇔ x = 25º
El ángulo buscado es de 25º.
1) Si un lado del triángulo mide un tercio del perímetro, el segundo 7 metros y el tercero un quinto del perímetro, ¿cuánto mide el perímetro del triángulo?
El perímetro de una figura geométrica es la suma de sus lados: p = a + b + c
Sea p el perímetro del triángulo.
Uno de los lados mide un tercio de p, luego: p/3
El tercer lado mide un quinto del p, luego: p/5
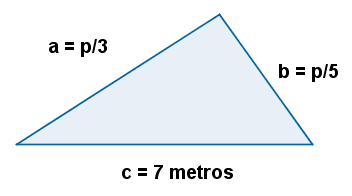
Como p es la suma de los lados del triángulo:
![]()
Resolvemos la ecuación de primer grado:
m.c.m.(3,5) = 15
15p = 5p + 3p + 15·7 ⇔ 15p = 8p + 105 ⇔ 7p = 105 ⇔ p = 15
El perímetro del triángulo mide 15 metros.
2) El área de un triángulo rectángulo es 96 cm2, y la diferencia entre la suma de los catetos y la hipotenusa es 8 cm. Halla los valores de los lados.
Sean x e y los valores de los catetos. Entonces, la hipotenusa mide: (x + y) - 8
El área del triángulo (rectángulo) es: xy/2 = 96
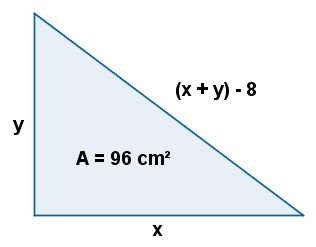
Por otro lado, aplicando el teorema de pitágoras tenemos: x2 + y2 = (x - y - 8)2
Tenemos por tanto el siguiente sistema a resolver:
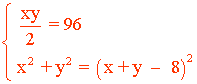
Simplificamos ambas ecuaciones:
xy/2 = 96 ⇔ xy = 192
x2 + y2 = (x - y - 8)2 ⇔ x2 + y2 = x2 + y2 + 64 + 2xy - 16x - 16y ⇔ 0 = 64 + 2xy - 16x - 16y ⇔ 16x + 16y - 2xy = 64
Como xy = 192 , la segunda ecuación queda:
16x + 16y - 2·192 = 64 ⇔ 16x + 16y - 384 = 64 ⇔ 16x + 16y = 448 ⇔ x + y = 28
Resolvemos el sistema mediante sustitución. Despejamos la variable x en la primera ecuación y sustituimos en la segunda:
xy = 192 ⇒ x = 192/y
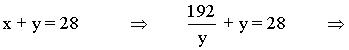
![]()
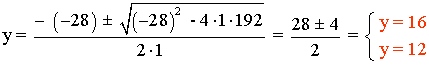
Si y = 16 ⇒ x = 192/y = 12
Si y = 12 ⇒ x = 192/y = 16
En ambos casos, la hipotenusa medirá lo mismo: x + y - 8 = 12 + 16 - 8 = 20
Por tanto, las medidas de los lados del triángulo son 12, 16 y 20 cm.
1) Si se disminuyen 4 metros al lado de un cuadrado, se obtiene otro de 128 m2 menos que el primero. ¿Cuánto medía el lado?
Sea x el lado que queremos calcular.
Entonces, el área del cuadrado de lado x es: x2
Si disminuimos en 4 metros el lado, tendremos un segundo cuadrado de lado x - 4 cuya área es: (x - 4)2
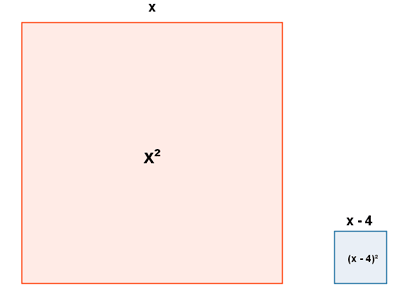
El segundo cuadrado mide 128 m2 menos que el primero, luego:
x2 - (x - 4)2 = 128
Resolvemos la ecuación:
x2 - (x - 4)2 = 128 ⇔ x2 - (x2 - 8x + 16) = 128 ⇔ 8x - 16 = 128 ⇔ 8x = 144 ⇔ x = 18
El lado medía 18 metros.
2) Los lados de dos cuadrados suman 131 m. Con sus diagonales se forma un rectángulo cuya área es 8540 m2. Hallar dichos lados.
Sea x el lado de uno de los cuadrados.
Entonces, el lado del segundo cuadrado medirá: 131 - x
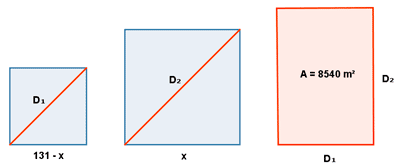
Aplicando el teorema de pitágoras, podemos calcular sus respectivas diagonales:
![]()
![]()
El rectángulo que forman ambas diagonales tiene un área de 8540 m2, luego:
D1 · D2 = 8540
2x · (131 - x) = 8540
Resolvemos la ecuación:
2x · (131 - x) = 8540 ⇔ 262x - 2x2 = 8540 ⇔ 2x2 - 262x + 8540 = 0
Dividiendo entre 2:
x2 - 131x + 4270 = 0
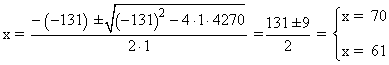
Si x = 70 ⇒ 131 - x = 61
Si x = 61 ⇒ 131 - x = 70
Los lados tienen que medir 70 y 61 metros respectivamente.
Un rectángulo mide 16 cm de ancho y 20 cm de largo. ¿Cuánto debe aumentar de ancho y disminuir de largo para que su área aumente en 22 cm2 y su perímetro en 2 cm?
Sea x lo que aumenta de ancho, y sea y lo que aumenta de largo.
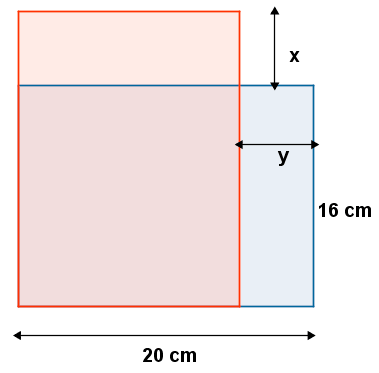
El rectángulo resultante medirá (16 + x) cm de ancho y (20 - y) cm de largo.
| Figura | Área | Perímetro |
|---|---|---|
| Primer rectángulo | 16 · 20 = 320 | 2·16 + 2·20 = 72 |
| Segundo rectángulo | (16 + x)(20 - y) | 2(16 + x) + 2(20 - y) |
El área del segundo rectángulo mide 22 cm2 más que el área del primero, luego: (16 + x)(20 - y) = 320 + 22
El perímetro del segundo rectángulo mide 2 cm más que el del primero, luego:; 2(16 + x) + 2(20 - y) = 72 + 2
Simplificamos ambas ecuaciones:
(16 + x)(20 - y) = 320 + 22 ⇔ 320 + 20x - 16y - xy = 342 ⇔ 20x - 16y - xy = 22
2(16 + x) + 2(20 - y) = 72 + 2 ⇔ 32 + 2x + 40 - 2y = 74 ⇔ 2x - 2y 72 = 74 ⇔ 2x - 2y = 2 ⇔ x - y = 1
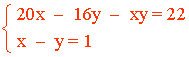
Resolvemos el sistema por el método de sustitución despejando la incógnita x de la segunda ecuación:
x - y = 1 ⇔ x = 1 + y
20x - 16y - xy = 22 ⇒ 20(1 + y) - 16y - (1 + y)y = 22 ⇒ 20 + 20y - 16y - y - y2 = 22 ⇒ y2 - 3y + 2 = 0
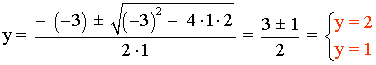
Si y = 2 ⇒ x = 1 + y = 3
Si y = 1 ⇒ x = 1 + y = 2
El problema tiene dos soluciones:
Aumentar el ancho en 3 cm y disminuir el largo en 2 cm .
Aumentar el ancho en 2 cm y disminuir el largo en 1 cm .
Los lados de un trapecio isósceles miden 5, 5, 5 y 13 metros respectivamente. ¿Cuál es el área del trapecio?
Un trapecio isósceles es aquel que tiene iguales dos de sus lados no paralelos. Recordamos que el área de un trapecio es:
![]()
Como dos de los lados del trapecio tienen que tener igual longitud, sus medidas serán 5 y 5. Las medidas restantes serán entonces las de las bases: 5 y 13
Para poder calcular su área nos falta conocer su altura, h.
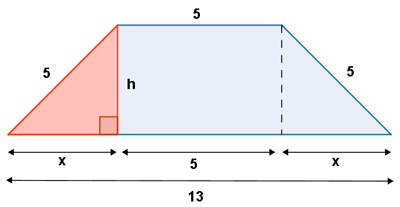
Observamos que: x + 5 + x = 13 ⇒ 2x = 8 ⇒ x = 4
Podemos calcular h usando el teorema de pitágoras en el triángulo rectángulo que aparece sombreado, para ello tendremos en cuenta que x = 4.
x2 + h2 = 52 ⇒ h2 = 52 - x2 = 25 - 16 = 9 ⇒ h = 3
Finalmente, el área del trapecio es:
![]()
El lado de un rombo es 5 cm y su área es 24 cm2. Calcula la longitud de sus diagonales.
El área de un rombo viene dado por:
![]()
Sea x su diagonal mayor e y su diagonal menor.

Como tenemos dos incógnitas, nos hace falta una segunda ecuación.
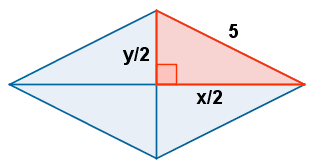
Podemos aplicar el teorema de Pitágoras al triángulo rectángulo que está sombreado en la figura.
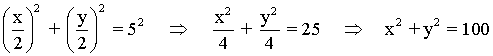
Reuniendo ambas ecuaciones tenemos el siguiente sistema:
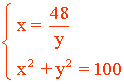
Lo resolvemos mediante el método de sustitución.
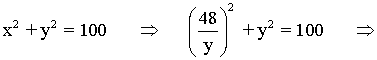
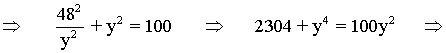
![]()
Se trata de una ecuación bicuadrática. Para resolverla hacemos el cambio de variable: z = y2
Nos queda una ecuación de segundo grado: z2 - 100z + 2304 = 0
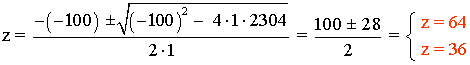
Si z = 64 ⇒ z = y2 ⇒ y = ±√z = ±√64 = ±8
Si z = 36 ⇒ z = y2 ⇒ y = ±√z = ±√36 = ±6
Las longitudes no pueden ser negativas, así que descartamos la solución negativa.
Si y = 8 ⇒ x = 48/y = 48/8 = 6
Si y = 6 ⇒ x = 48/y = 48/6 = 8
Como x es la diagonal mayor medirá 8 cm , y por tanto, la diagonal menor y mide 6 cm.
Sean dos cubos cuyas aristas difieren en 2 cm y sus volúmenes en 56 cm3. Halla el valor de las aristas.
Sea x el lado del cubo pequeño. Su volúmen es: x3
Sea x + 2 el lado del cubo grande. Su volúmen es: (x + 2)3
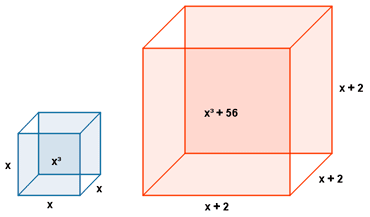
Sus dos volúmenes difieren en 56 cm3, luego:
(x + 2)3 - x3 = 56
Resolvemos la ecuación:
(x + 2)3 - x3 = 56 ⇒ (x3 + 6x2 + 12x + 8) - x3 = 56 ⇒ 6x2 + 12x + 8 = 56 ⇒ 6x2 + 12x - 48 = 0 ⇒ x2 + 2x - 8 = 0
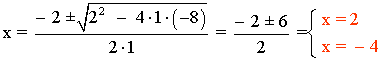
Como la longitud de las aristas no puede ser negativa, descartamaos la solución x = - 4. Por tanto, si x = 2, el lado del cubo grande mide x + 2 = 4 cm.
Los lados de los cubos son 2 y 4 cm.
Los perímetros de las caras de un orotoedro son 54, 80 y 98 cm, respectivamente. Halla los lados, el área total y el volumen del ortoedro.
El perímetro de una figura geométrica es la suma de sus lados.
Sean x, y, z el ancho, el largo y el alto del tetraedro respectivamente.
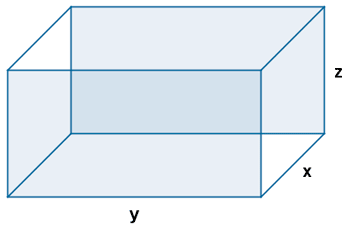
Un tetraedro tiene tres caras distintas. Para escribir la ecuación del perímetro de cada cara contamos sus respectivas aristas. Tendremos por tanto tres ecuaciones (una por cada cara):

Resolvemos el sistema por el método de reducción:
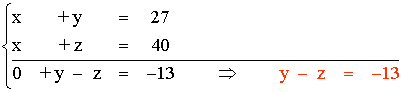
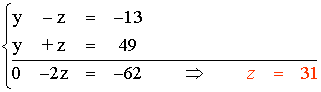
Si z = 31 ⇒ y - z = - 13 ⇒ y = - 13 + z = - 13 + 31 = 18
Si y = 18 ⇒ x + y = 27 ⇒ x = 27 - y = 27 - 18 = 9
Los lados del ortoedro son: x = 9 , y = 18 , z = 31
El área del tetraedro es la suma de las áreas de los lados:
A = 2xy + 2xz + 2yz = 2 · 9· 18 + 2 · 9 · 31 + 2 · 18 · 31 = 1998 cm2
El volúmen del tetraedro es:
V = xyz = 9· 18 · 31 = 5022 cm3
Con una cartulina de 240 cm2 de superficie hacemos un prisma de base cuadrada, sin bases, cuyo volumen es de 360 cm3. ¿Cuáles son las dimensiones de la cartulina?
Sean x e y las dimensiones de la cartulina.
El área de la cartulina es: xy = 240
Si formamos un prisma sin base el largo de la cartulina (x) queda dividido en cuatro partes, una para cada cara del prisma.
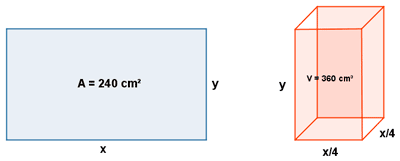
Por tanto, tendremos un prisma cuyas dimensiones serán x/4 , x/4 e y de largo, ancho y alto respectivamente.
El volumen del prisma es: x/4 · x/4 · y = 360
Nos queda el siguiente sistema a resolver:
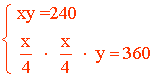
Aplicamos el método de igualación despejando la variable y en ambas ecuaciones:
![]()
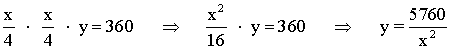
Igualamos ambos resultados:
![]()
![]()
![]()
Como x ≠ 0 , necesariamente: 240x - 5760 = 0 ⇔ 240x = 5760 ⇔ x = 24 cm
Si x = 24 ⇒ y = 240/x = 10 cm
La cartulina mide 24 cm de largo y 10 cm de alto.


 INICIO
INICIO