Números complejos
Necesidad de ampliar los números reales
Las progresivas ampliaciones de los conjuntos numéricos han sido necesarias para resolver ecuaciones algebráicas cada vez más complicadas:
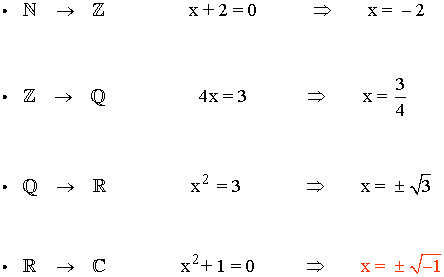
Ejemplos:
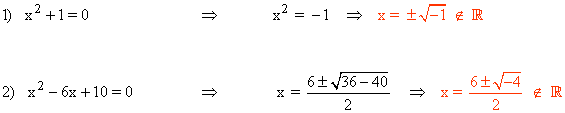
En algunas ocasiones, al resolver ecuaciones de segundo grado, las soluciones que obtenemos no son soluciones reales:
La unidad imaginaria
La unidad imaginaria se representa con la letra i y su valor es:
![]()
Ejemplos:
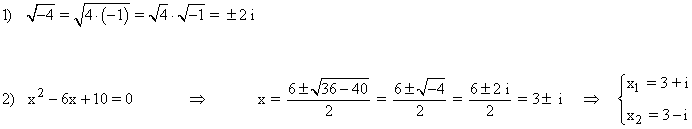
Número complejo en forma binómica
Se llama número complejo en forma binómica a la siguiente expresión:
![]()
• El número a recibe el nombre de parte real y se representa por a = Re(z)
• El número b recibe el nombre de parte imaginaria y se representa por b = Im(z)
Conjunto de los números complejos
El conjunto de los números complejos se define a partir del conjunto de los números reales, de la siguiente forma:
![]()
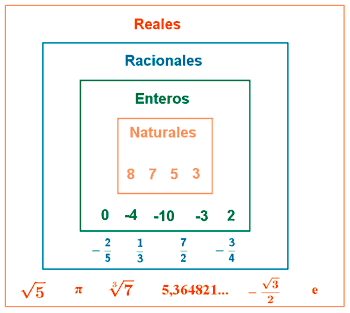

Ejemplos:

Igualdad de números complejos
Dos números complejos son iguales si sus partes reales e imaginarias coinciden:
Ejemplo:
Halla x e y para que se verifique la siguiente igualdad: x + 5 i = - 3 + y i
Para que los dos números complejos sean iguales tiene que verificarse que x = -3 e y = 5
Representación gráfica de los números complejos
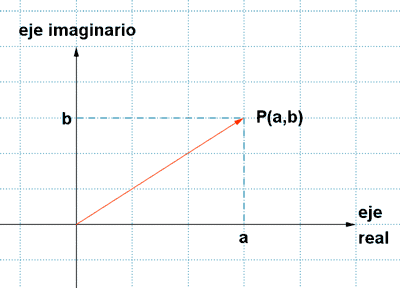
Los números complejos se representan en los ejes cartesianos:
• El eje OX se llama eje real
• El eje OY se llama eje imaginario
El número complejo z = a + b i se representa con el punto (a, b) que recibe el nombre de afijo o bien mediante un vector con origen el punto (0, 0) y extremo (a, b).
Los afijos de los números reales se sitúan sobre el eje real (OX), mientras que los imaginarios puros se representan sobre el eje imaginario (OY).
Ejemplos:
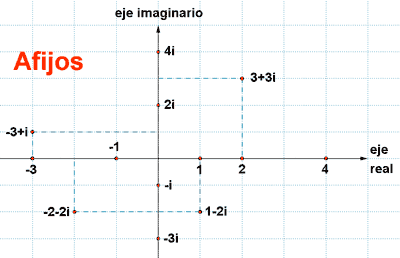
1) Representa los siguientes números complejos mediante sus afijos:
- 3 , - 1 , 1 , 2 , 4 , - 3 i , - i , 2 i , 4 i , 3 + 3 i , - 3 + i , - 2 - 2 i , 1 - 2 i
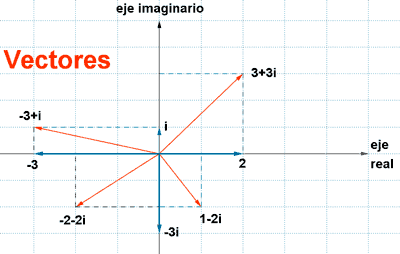
2) Representa los siguientes números complejos mediante sus vectores:
- 3 , 2 , - 3 i , i , 3 + 3 i , - 3 + i , - 2 - 2 i , 1 - 2 i
3) Dados los siguientes números complejos, halla sus afijos:
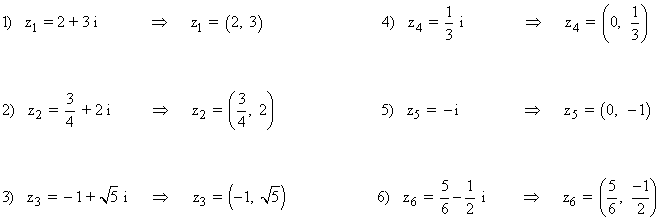


 INICIO
INICIO
