Determinación de una recta
Vector director de una recta
El vector director de una recta es un vector cualquiera que está en la recta o bien es paralelo a dicha recta. Se representa por:
![]()
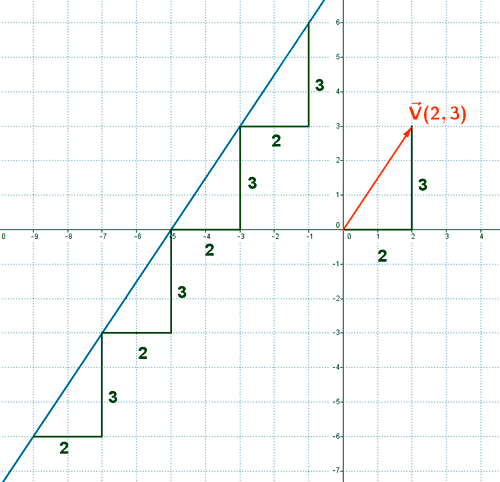
El vector v(2,3) significa que por cada dos unidades que aumenta x , la y aumenta tres unidades.
La recta por tanto es creciente.
De un vector director solamente nos interesa su dirección, no su longitud. Por tanto, siempre podemos simplificarlo.
Por ejemplo:
v(8, 12) || v(4, 6) || v(2, 3)
Todos los vectores anteriores representan al mismo vector director.
Determinación de una recta
Una recta queda determinada de dos formas diferentes:
• Dando un punto A y un vector director v
• Dados dos puntos A y B
Recta determinada por un punto y un vector
Es la recta que pasa por el punto y es paralela al vector director
Ejemplo:
Dibuja la recta que pasa por el punto (3, 3) y tiene como vector director v(2, 1)
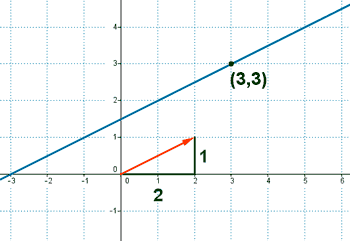
Recta determinada por dos puntos
El vector director de esta recta es:
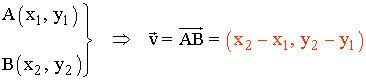
Ejemplo:
Dibuja la recta que pasa por los puntos A(-1, 4) y B(2, 2). Calcula y dibuja un vector director.
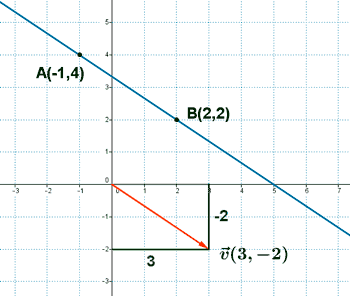
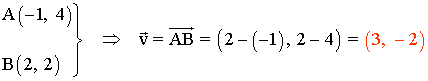
Condición para que tres puntos estén alineados

Ejemplo:
1) Demuestra que los puntos A(-1, 4) , B(2, 2) y C(5, 0) están alineados.
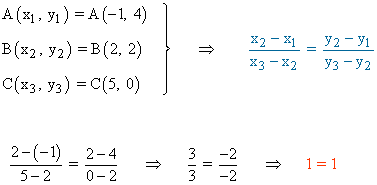
2) Determina el valor de k para que los puntos A(2 , -1) , B(1 , 4) y C(k , 9) estén alineados.
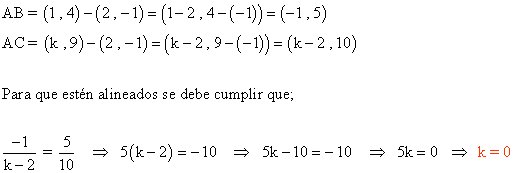
Pendiente de una recta
La pendiente de la recta es la tangente del ángulo que forma el semieje positivo de la X con la recta. Es decir, la pendiente del vector director de la recta. Se representa con la letra m.
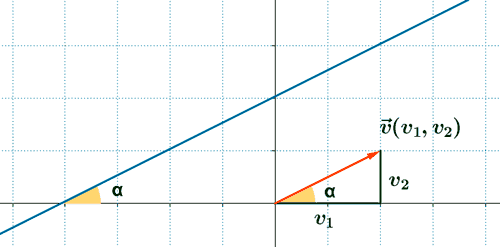
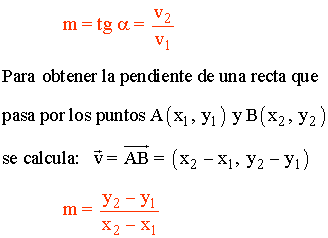
Ejemplo:
Dibuja la recta que pasa por los puntos A(-5, 1) y B(1, 4) y calcula su pendiente.
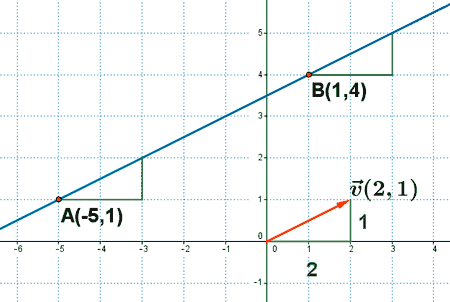
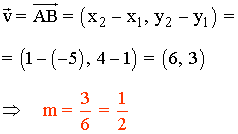
El vector v(2, 1) o la pendiente m = 1/2 indican que por cada dos unidades que aumenta la x, y aumenta en una unidad.
Por lo tanto, la recta es creciente.
Vector perpendicular o normal a una recta
Un vector normal a una recta es cualquier vector que sea perpendicular a dicha recta. Para calcular un vector normal a una recta tomamos las coordenadas del vector director, cambiamos su orden, y a una de ellas le cambiamos el signo:
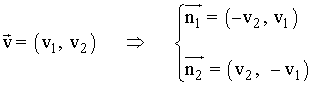
Ejemplos:
1) Calcula y dibuja un vector perpendicular a la recta que pasa por el punto A(-4, 2) y tiene como vector director v(1, -2).
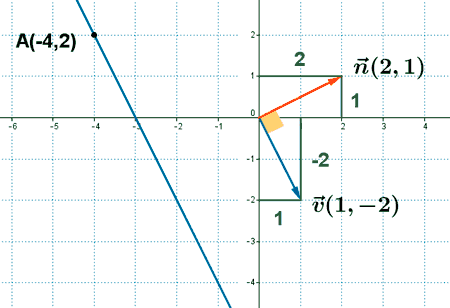
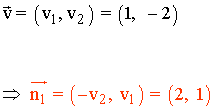
2) Calcula dos vectores directores de una recta cuyo vector normal es n(2, 1).
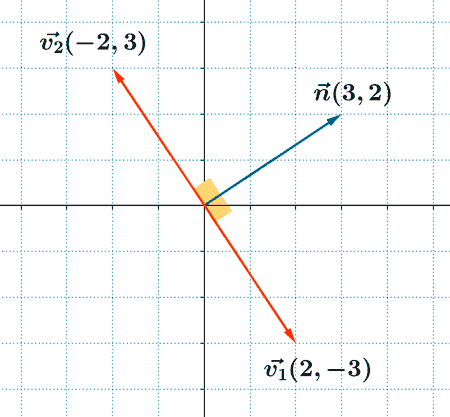
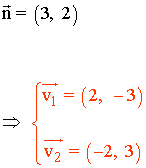


 INICIO
INICIO
