Problemas resueltos de perímetros y áreas de triángulos.
| Nombre | Dibujo | Perímetro | Área |
|---|---|---|---|
| Triángulo rectángulo |
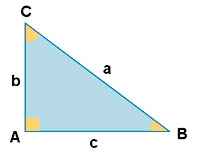 |
Teorema de Pitágoras: a2 = b2 + c2 P = a + b + c |
|
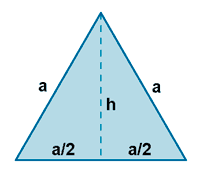
| Triángulo equilátero |
 |
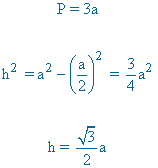 |
 |
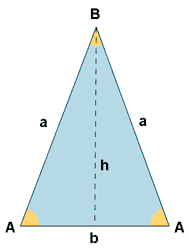
| Triángulo isósceles |
 |
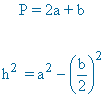 |
|
| Triángulo escaleno | 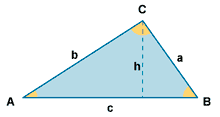 |
P = a + b + c |
1 ) En un triángulo rectángulo se conocen la hipotenusa a = 5m y un cateto b = 4 m. Calcula el lado desconocido.
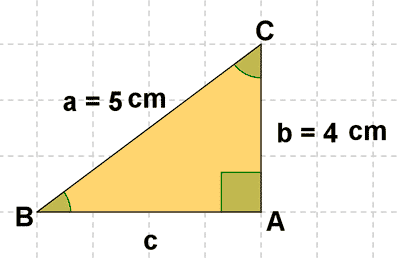
![]()
2 ) En un triángulo rectángulo se conocen los catetos b =8m y c =6 m. Calcula el lado desconocido.
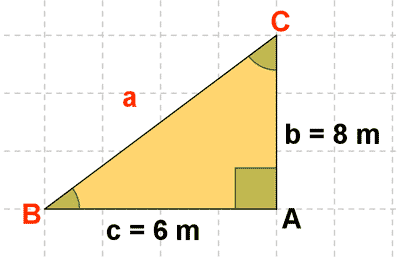
![]()
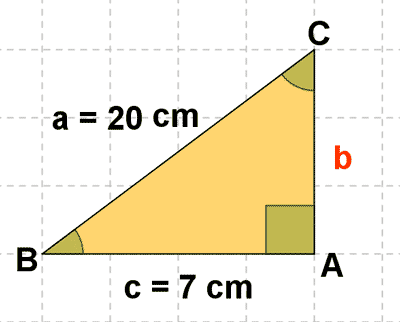
3 ) En un triángulo rectángulo se conocen los catetos a = 20 cm y c = 7 cm. Calcula el lado desconocido.
![]()
4 ) Calcular el perímetro y el área de las siguientes figuras.
a )
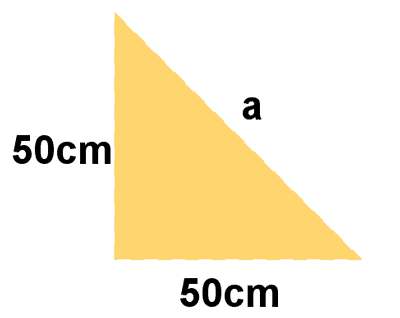
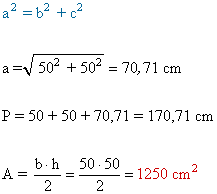
b )
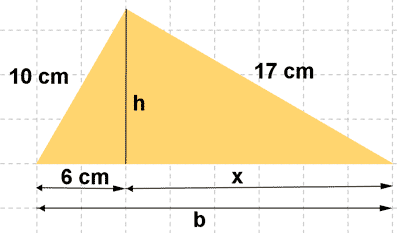
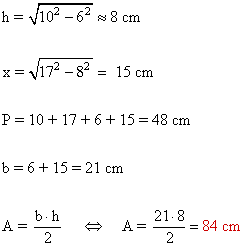
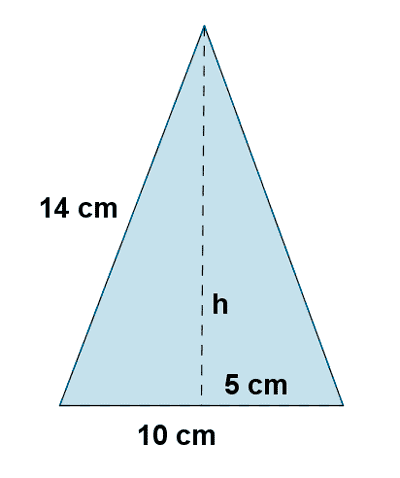
5 ) Hallar el área de un triangulo isósceles en el que los lados iguales miden 14 m cada uno y el desigual mide 10 m
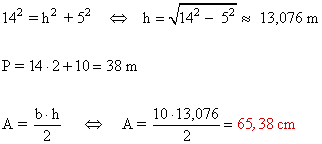
6 ) Calcula el área y el perímetro de las siguientes figuras.
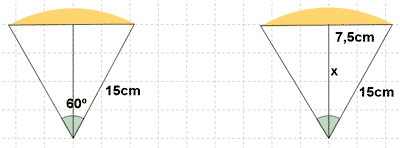
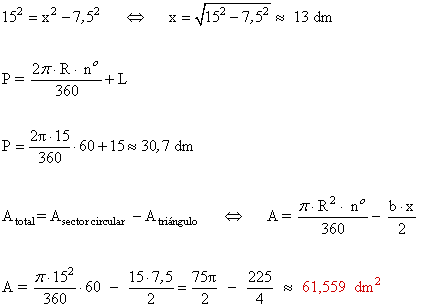
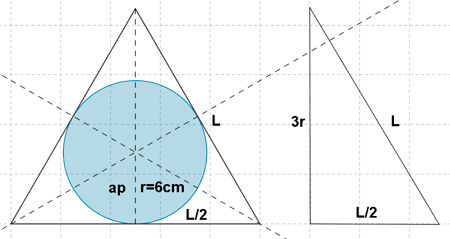
7 ) Calcular el lado y la apotema de un triángulo equilatero circunscrito en una circunferencia de 6 cm de radio.
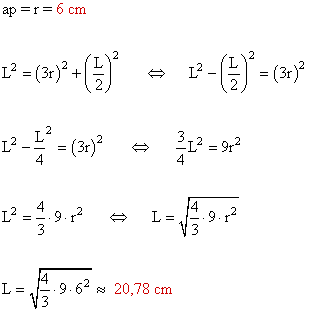
8 ) Calcular el diámetro de la circunferencia inscrita en el triángulo.
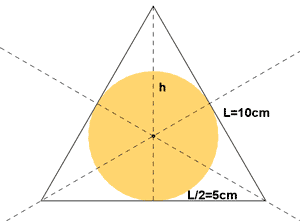
Como tenemos un triángulo equilátero sabemos que sus medianas coinciden con sus alturas y sus bisectrices. Por tanto, el baricentro coincide con el incentro. Entonces se deduce que el diámetro de la circunferencia inscrita en el triángulo es 2/3 de la altura h.
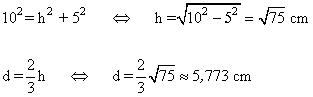
9 ) La longitud de la circunferencia inscrita a un triángulo equilatero es 10 cm.
a) ¿Cúanto mide la circunferencia circunscrita?
b) ¿Cúal es el perímetro del triángulo?
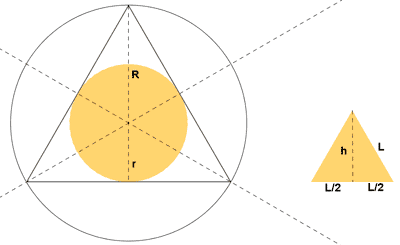
Estamos ante un triángulo equilátero luego las bisectrices, medianas, mediatrices y alturas coinciden. A su vez el baricentro, ortocentro, circuncentro e incentro también coinciden. Se sabe también que el radio de la circunferencia circunscrita es el doble del radio de la circunferencia inscrita. Por tanto, la longitud de la circunferencia es el doble.
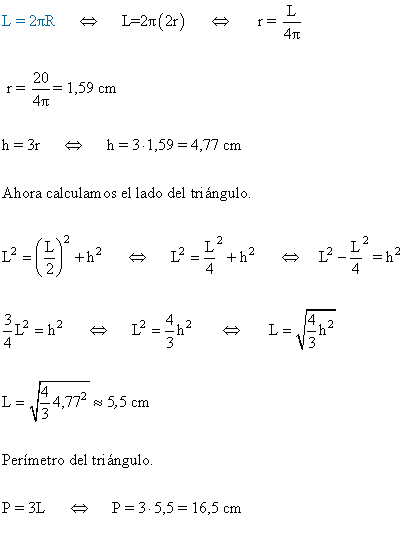
10 ) Calcula y dibuja acerca del dibujo adjunto los siguientes apartados:
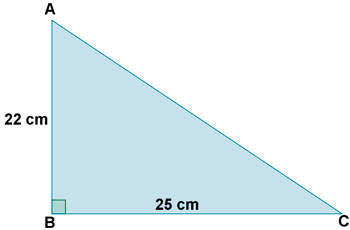
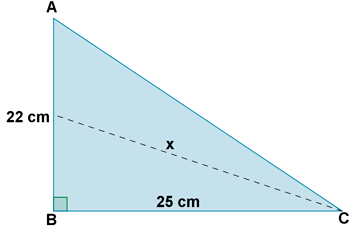
a ) Dibujar la mediana que sale de C y halla su longitud.
b ) Dibujar las mediatrices y hallar el radio de la circunferencia circunscrita.
c ) ¿Cúal es el ortocentro de ese triángulo?
a )
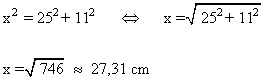
b )
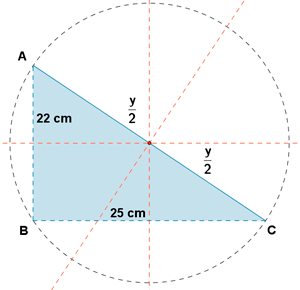
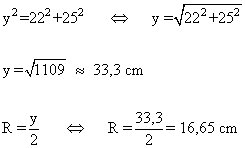
Las mediatrices se cortan en los circunscritos que para este caso en concreto es el punto medio de la hipotenusa. (Llamamos y a la longitud de la hipotenusa).
c )
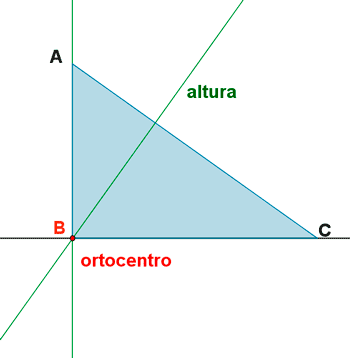
El ortocentro es el punto donde se unen las tres alturas. En nuestro caso es el vértice B.
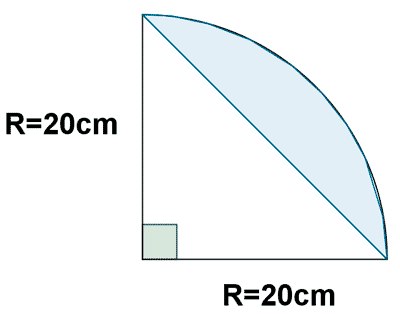
11 ) Calcula el área de un segmento circular de 90º de amplitud en un círculo de 20 cm de radio.
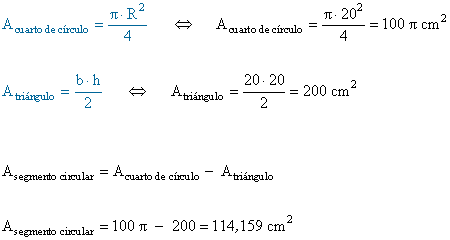
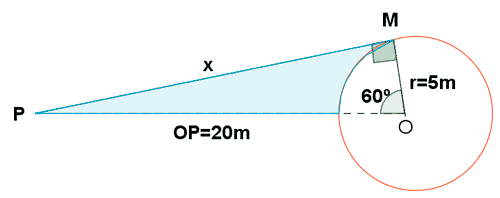
12 ) Calcular:
a) La longitud de x
b) El área de la parte coloreada.
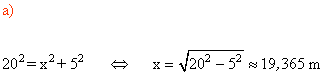
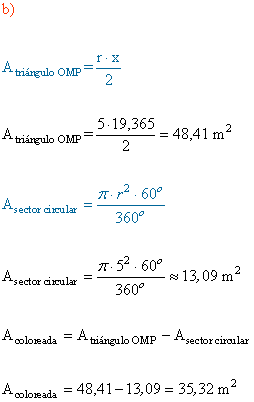
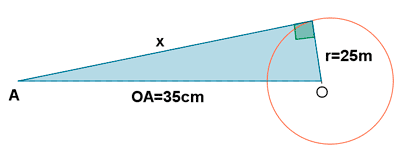
13-a ) Desde cierto punto A que dista 35 cm del centro de una circunferencia de radio 25 cm, se traza una tangente. Calcular la distancia desde A hasta el punto de tangencia
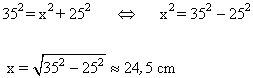
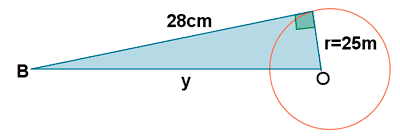
13-b ) Realizamos otra tangente desde otro punto B y al medir la distancia de P al punto de tangencia obtenemos 28 cm. ¿Cúal es la distancia de B al centro de la circunferencia?
![]()
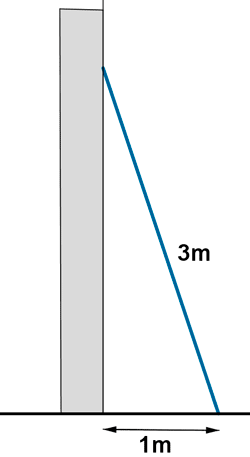
14 ) ¿ A que altura se llega con una escalera de 3 metros si colocamos su base a 1 metro de la pared?
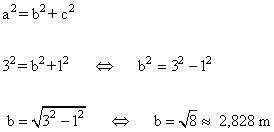
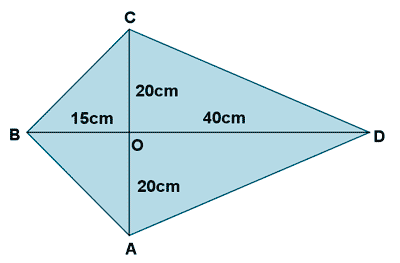
15 ) Las diagonales de una cometa ABCD se cruzan perpendicularmente en el punto O. Si OA mide 20 cm, OC 20 cm, OD 40cm y OB 15 cm, calcule la medida de los lados de la cometa.
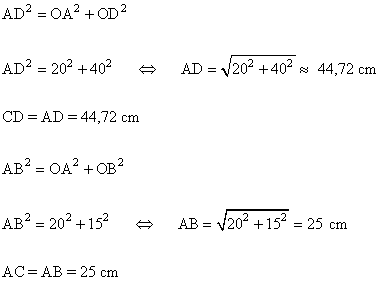


 INICIO
INICIO