Fórmulas de áreas y volumenes de cuerpos geométricos
Área y volumen de los poliedros regulares
| Dibujo | Área | Volumen | |
|---|---|---|---|
| Hexaedro o cubo | 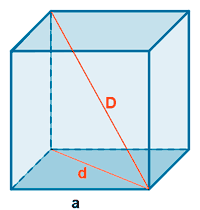 |
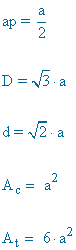 |
ap = apotema D = diagonal Ac = área cara At = área total V = a3 |
| Tetraedro | 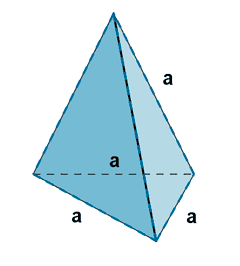 |
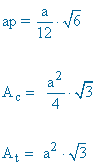 |
|
| Octaedro | 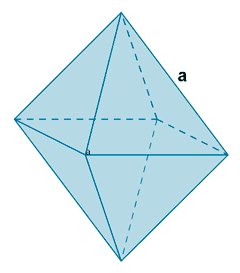 |
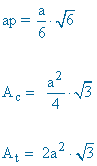 |
|
| Icosaedro | 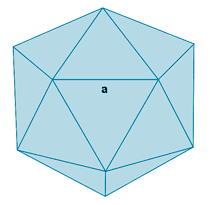 |
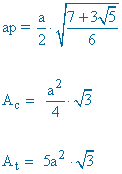 |
|
| Dodecaedro | 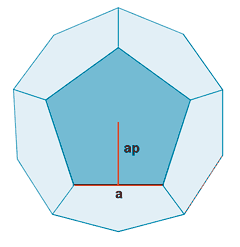 |
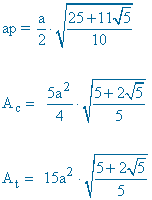 |
Teorema de Euler
C + V = A + 2
| Nombre | Cara | Nº de caras | Nº de vértices | Nº de aristas |
|---|---|---|---|---|
| Hexaedro o cubo | Cuadrado | 6 | 8 | 12 |
| Tetraedro | Triángulo | 4 | 4 | 6 |
| Octaedro | Triángulo | 8 | 6 | 12 |
| Icosaedro | Triángulo | 20 | 12 | 30 |
| Dodecaedro | Pentágono | 12 | 20 | 30 |
Área y volumen de los poliedros irregulares
(cuerpos geométricos limitados por polígonos)
| Dibujo | Área | Volumen | |
|---|---|---|---|
| Ortoedro | 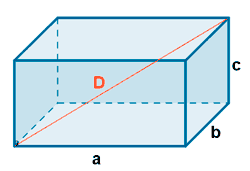 |
A t = 2·(a·b + a·c + b·c) |
V = a·b·c |
| Prisma triangular | 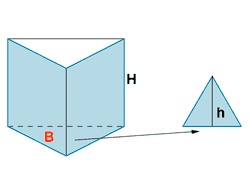 |
AL = PB·h AT = AL + 2·AB |
ap = apotema PB = perímetro de la base AL = área lateral AB = área base AT = área total |
| Prisma cuadrangular | 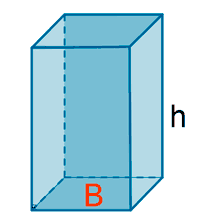 |
AL = PB·h
AT = AL + 2·AB |
V = A base · h |
| Prisma pengatonal | 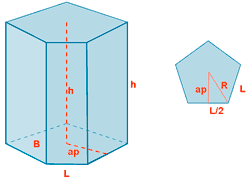 |
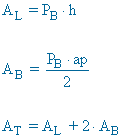 |
V = A base · h |
| Prisma hexagonal | 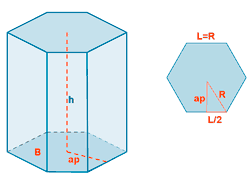 |
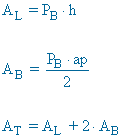 |
V = A base · h |
| Pirámide cuadrangular | 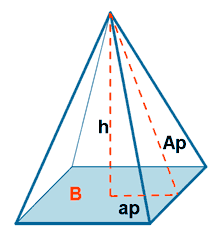 |
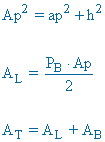 |
PB = perímetro base
|
| Pirámide pentagonal | 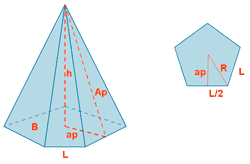 |
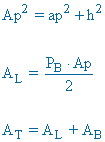 |
|
| Pirámide hexagonal | 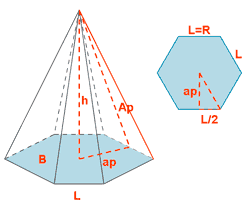 |
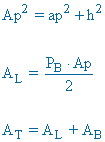 |
|
| Tronco de piramide cuadrangular | 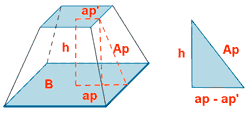 |
P = perímetro base mayor p = perímetro base menor 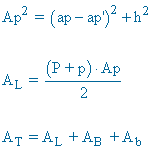 |
ap = apotema tronco AB = área base mayor Ab = área base menor |
| Tronco de piramide hexagonal | 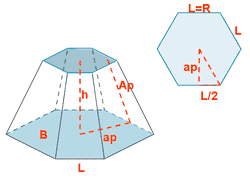 |
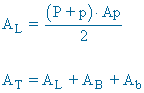 |
Área y volumen de cuerpos de revolución
| Dibujo | Área | Volumen | |
|---|---|---|---|
| Cilindro circular | 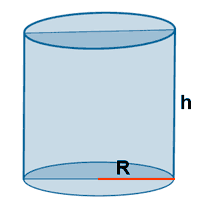 |
AL = 2π·R·h AB = π ·R2 AT = AL + 2·AB AT = 2π·R·(h + R) |
V = AB·h V = π·R2·h |
| Cilindro circular hueco | 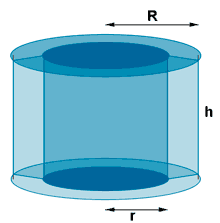 |
AB = π ·(R2 - r2) | V = AB·h V = π·(R2- r2)·h |
| Cono | 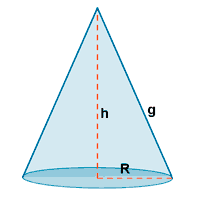 |
g2 = R2 + h2 AL = π·R·g AB = π·R2 AT = π·R·(g + R) |
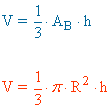 |
| Tronco de cono |
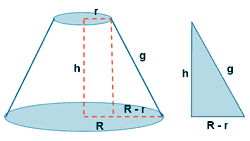 |
g2 = (R - r)2 + h2 AL = π·g·(R + r) AB = π·R2 Ab = π·r2 AT = AL + AB + Ab AT = π·[g·(R + r) + R2 + r2] |
Área y volumen de cuerpos esféricos
| Dibujo | Área | Volumen | |
|---|---|---|---|
| Esfera | 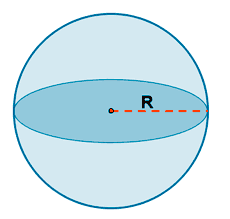 |
|
|
| Casquete esférico | 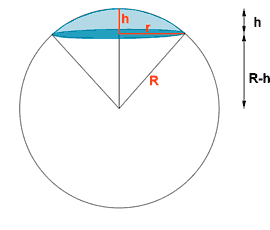 |
R2 = r2 + (R - h)2 |
|
| Sector esférico | 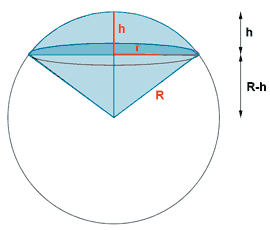 |
R2 = r2 + (R - h)2 |
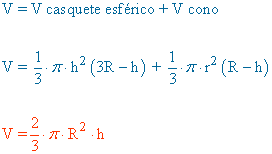 |
| Zona esférica | 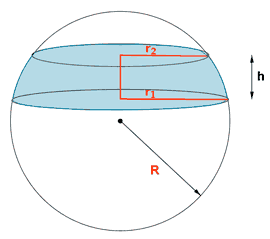 |
||
| Huso y cuña esférica | 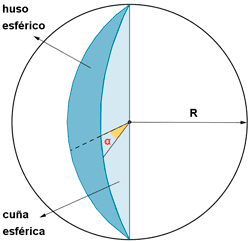 |
Área huso esférico: |
Volumen cuña esférico: |


 INICIO
INICIO