INICIOIntegrales racionales II:
Raíces reales simples
Que el grado del polinomio del numerador sea menor que el grado del polinomio del denominador y las raíces sean reales y distintas.
Toda fracción racional propia se puede expresar como suma de fracciones más simples.
Si tenemos dos raíces reales distintas x = x1 y x = x2 , la descomposición es la siguiente:
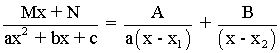
Tiene n raíces reales distintas x = x1 , x = x2 , x = x3 ... x = xn
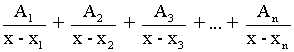
Ejemplo raíces reales distintas:
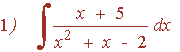
El denominador tiene dos raíces reales distintas: x1 = 1 y x2 = 2
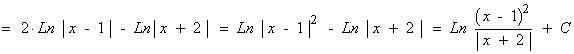
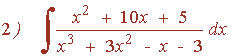
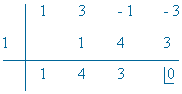
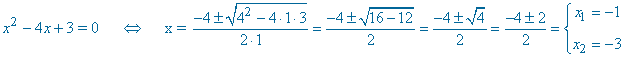
El denominador tiene tres raíces reales distintas: x1 = 1 , x2 = -1 y x3 = -3
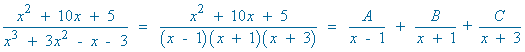
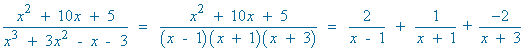
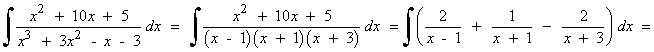
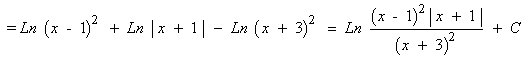
Se pueden separar los numeradores pero no los denominadores
