Integración de funciones racionales inmediatas
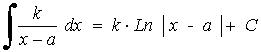
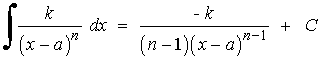
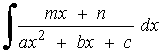
La última integral es inmediata si el denominador tiene raíces complejas.
![]()
Se pueden separar los numeradores pero no los denominadores
Ejemplos de la forma logarítmica:
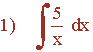
![]()
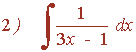
![]()
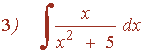
![]()
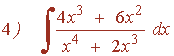
![]()
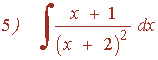
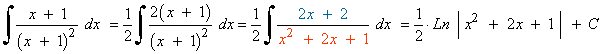
Ejemplos de la forma potencial:
![]()
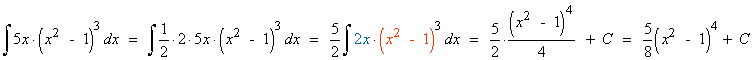
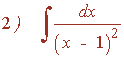
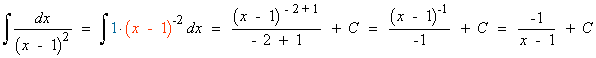
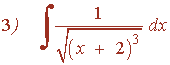
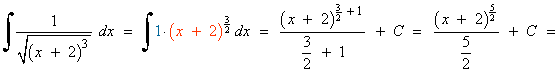
![]()
Ejemplos de la forma logaritmo más arcotangente:
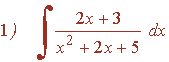
El denominador no tiene raíces reales, por lo que no se puede descomponer en factores lineales. Tiene dos raíces imaginarias: x1 = - 1 - 2i y x2 = - 1 + 2i
Completamos el cuadrado:
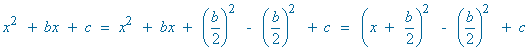
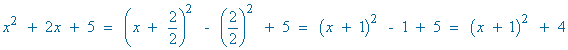
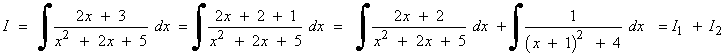
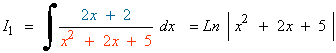
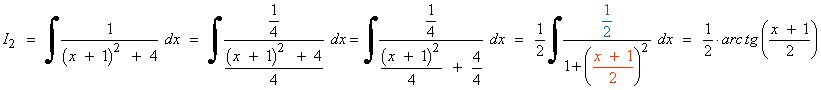
![]()
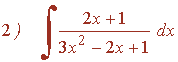
El denominador no tiene raíces reales, por lo que no se puede descomponer en factores lineales. Tiene dos raíces imaginarias: x1 = - 1 - 2i y x2 = - 1 + 2i
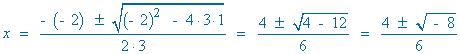
En este caso, al tener el denominador raíces imaginarias, buscamos la derivada del denominador mediante la siguiente descomposición:
(3x2 - 2x + 1 ) ' = 6x - 2
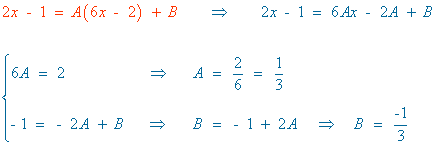
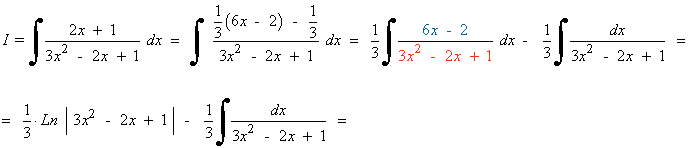
Completamos el cuadrado:
![]()
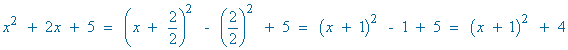
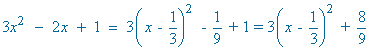
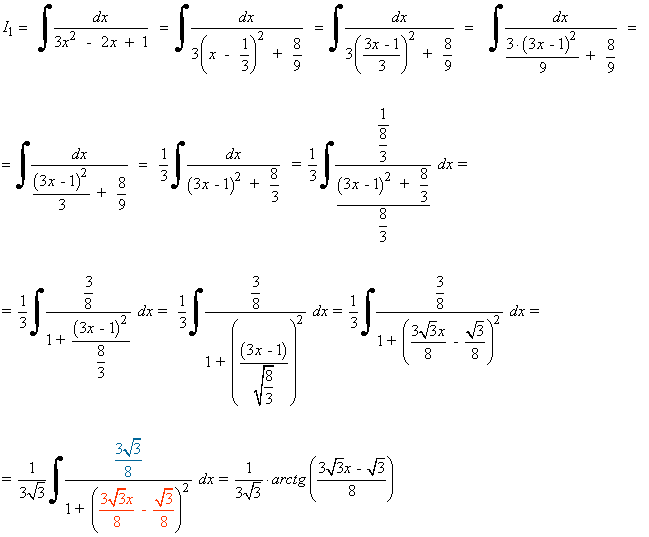


 INICIO
INICIO

