Ejercicios resueltos de integrales racionales II : raíces imaginarias simples y múltiples
Haga click en la correspondiente pestaña para ver la solución del ejercicio
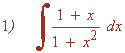
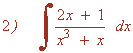
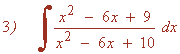
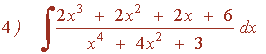
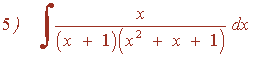
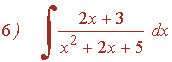
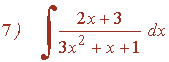
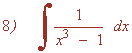
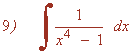
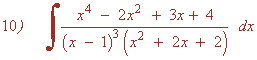
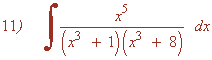
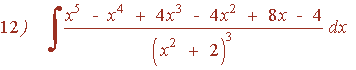
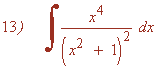
![]()
![]()
Se pueden separar los numeradores pero no los denominadores
Resuelve las siguientes integrales racionales:
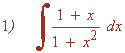
Las raices del denominador son imaginarias: x = ± √-1 = ± i
Resolvemos la integral descomponiendola en dos sumas:
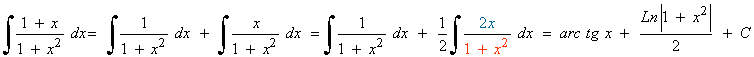
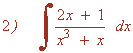
Podemos factorizar el denominador así:
x3 + x = x(x2 + 1)
Luego las raíces de x3 + x = 0 son : 0 , ±√-1
Son tres raíces: una real simple y dos complejas simples.
Por tanto:
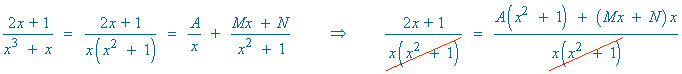
Como los denominadores son iguales, los numeradores también tienen que ser iguales:
![]()
Para x = 0 : 1 = A
Para x = 1 : 3 = 2A + M + N ⇒ 3 = 2 + M + N ⇒ M + N = 1
Para x = -1 : -1 = 2A + M - N ⇒ -1 = 2 + M - N ⇒ M - N = -3
Resolviendo el sistema se tiene: M = - 1 , N = 2
![]()
![]()
Resolviendo las integrales inmediatas y aplicando las propiedades de los logaritmos:
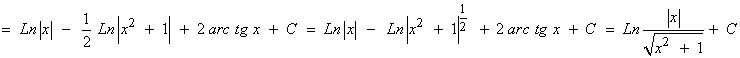
SELECTIVIDAD
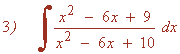
Como numerador y denominador tienen mismo grado, realizamos la división y aplicamos la fórmula del cociente:
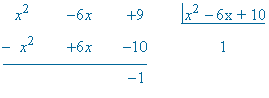
![]()
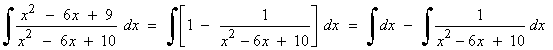
La primera integral es inmediata. La segunda es de tipo racional, por lo que calculamos las raices del denominador y después lo factorizamos:
![]()
![]()
![]()
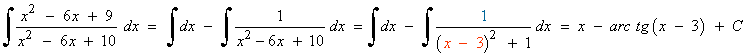
Resuelve la siguiente integral racional:
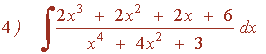
![]()
![]()
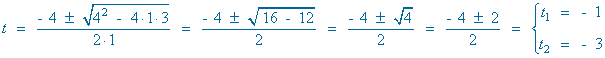
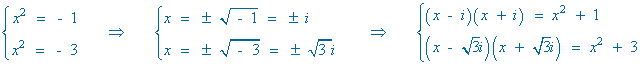
![]()
![]()
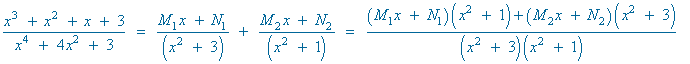
![]()
![]()
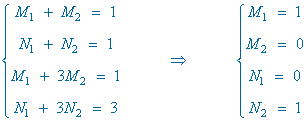
![]()
![]()
![]()
![]()
![]()
Resuelve la siguiente integral racional:
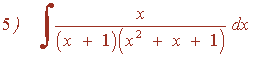
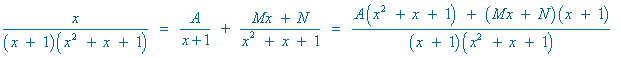
![]()
![]()
![]()
![]()
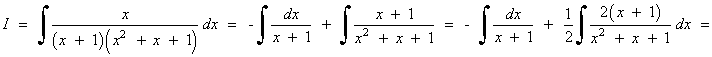
![]()
![]()
![]()
![]()
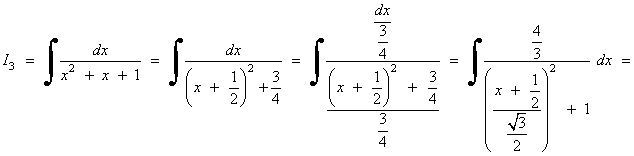
![]()
![]()
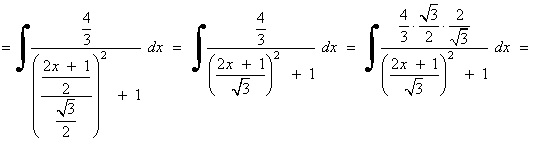
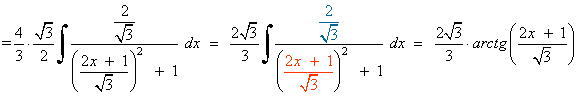
![]()
Resuelve la siguiente integral racional:
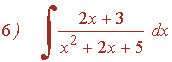
Calculamos las raices del denominador:
x2 + 2x + 5 = 0 ⇒ x1 = - 1 + 2i , x2 = - 1 - 2i
El denominador no tiene raíces reales, por lo que no se puede descomponer en factores lineales.
Tiene dos raíces imaginarias: x1 = - 1 - 2i y x2 = - 1 + 2i
Ver integrales racionales.
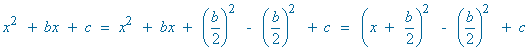
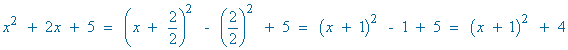
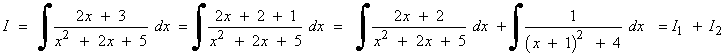
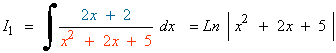
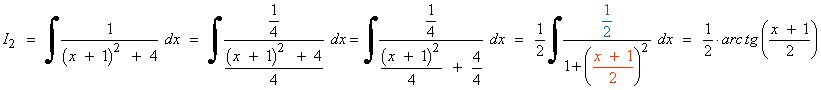
![]()
Resuelve la siguiente integral racional:
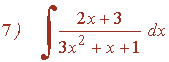
Calculamos las raices del denominador:
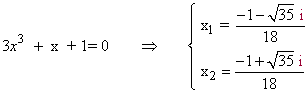
Son raíces complejas simples, por lo que calculamos la integral del siguiente modo:
Ver integrales racionales.
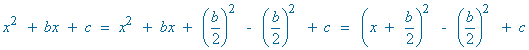
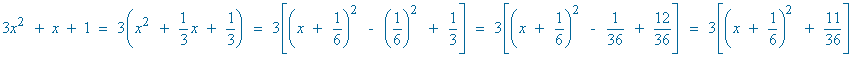
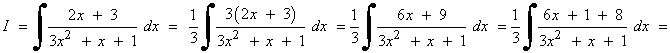
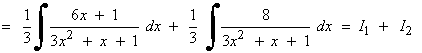
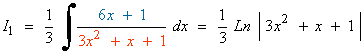
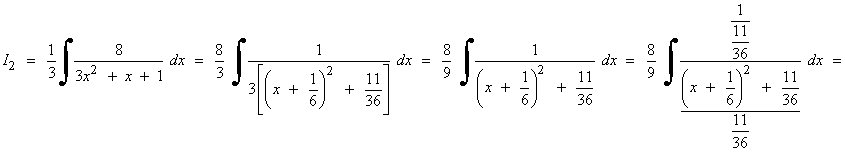
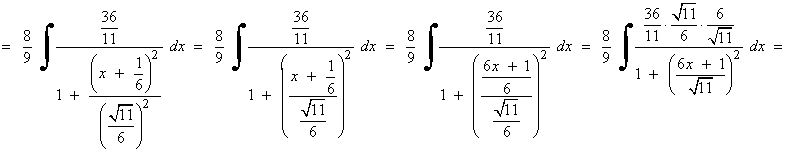
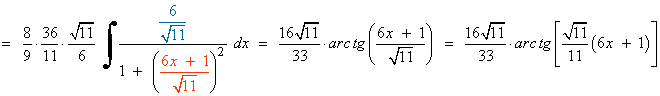
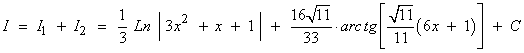
SELECTIVIDAD
Resuelve la siguiente integral racional:
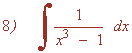
Factorizamos el denominador aplicando Ruffini:
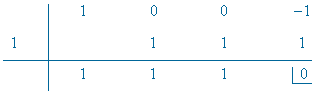
x3 - 1 = (x - 1)(x2 + x + 1)
El denominador tiene tres raíces:
una real simple y dos complejas simples.
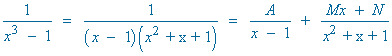
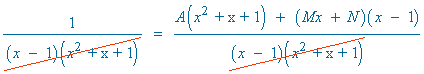
![]()
Para x = 1 : 1 = 3A ⇒ A = 1/3
Para x = 0 : 1 = A - N ⇒ N = - 2/3
Para x = - 1 : 1 = A + 2M - 2N ⇒ M = - 1/3
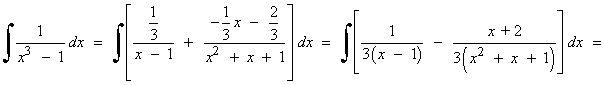
![]()
![]()
![]()
![]()
![]()
Completamos cuadrados en el denominador:
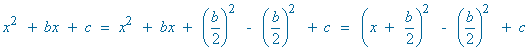
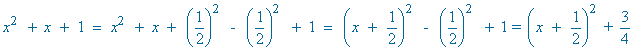
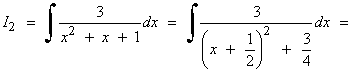
Para poder aplicar la regla del arcotangente necesitamos un 1 en lugar de 3/4 , por tanto dividimos entre 3/4 numerador y denominador:
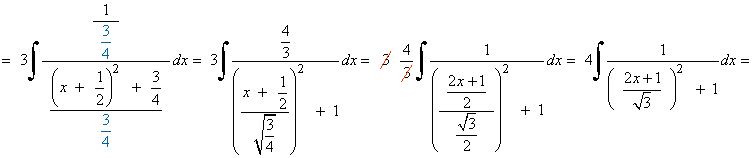
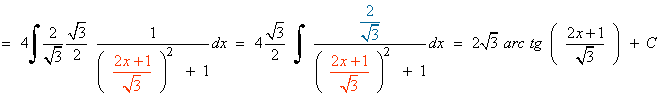
Solución de I1 :
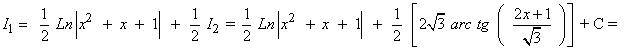
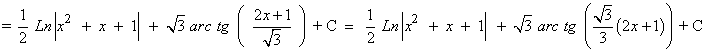
Solución final:
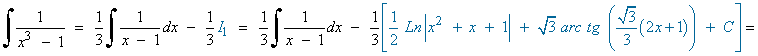
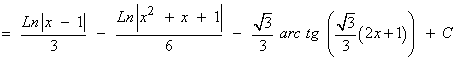
Resuelve la siguiente integral racional:
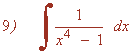
Factorizamos el denominador:
x4 - 1 = x4 - 12 = (x2 - 1)(x2 + 1) = (x - 1)(x + 1)(x2 + 1)
Tiene cuatro raíces, dos de ellas reales simples y las otras dos complejas simples:
x1 = 1 , x2 = -1 , x3 = -√-1 = - i , x4 = √-1 = i
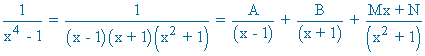
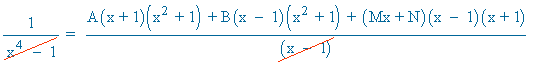
![]()
Para x = 1 : 1 = 4A ⇒ A = 1/4
Para x = -1 : 1 = - 4B ⇒ B = - 1/4
Para x = 0 : 1 = A - B - N ⇒ 1 = 1/4 + 1/4 - N ⇒ N = - 1/2
Para x = 2 : 1 = 15A + 5B + 6M + 3N ⇒ 1 = 15/4 - 5/4 + 6M - 3/2 ⇒ M = 0
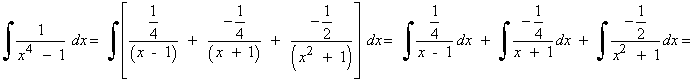
![]()
Resuelve la siguiente integral racional:
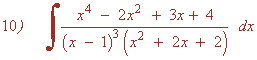
Las raíces del denominador son:
x1 = 1 (triple) , x2 = -1 - i , x3 = -1 + i
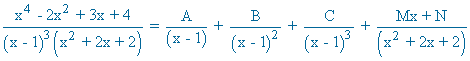
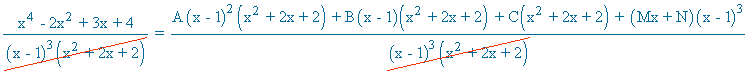
![]()
![]()
![]()
![]()
![]()
Identificamos, en ambos miembros de la igualdad, los coeficientes de x4 , x3 , x2 , x y termino independiente:
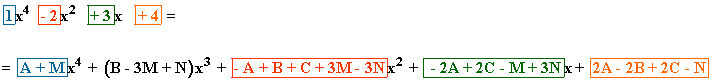
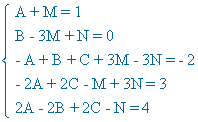
Resolviendo el sistema se obtiene:
![]()
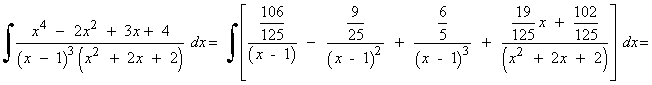
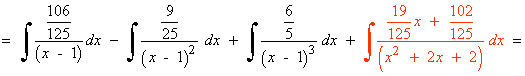
![]()
Resolvemos la integral I1 :
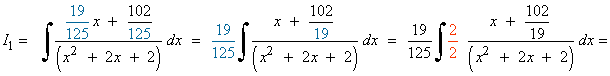
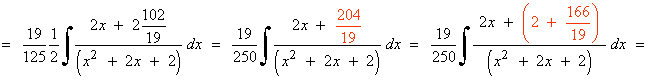
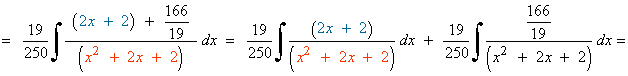
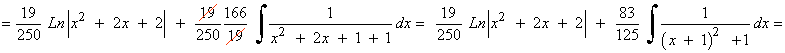
![]()
Solución final:
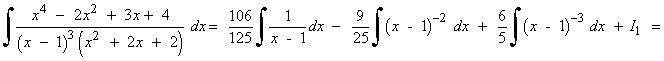
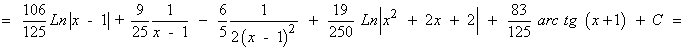
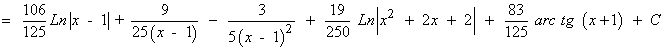
Resuelve la siguiente integral racional:
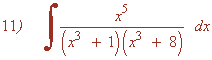
Calculamos las raíces del denominador:
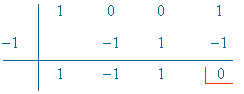
x3 + 1 = (x + 1)(x2 - x + 1)
Tiene una raiz real y dos imaginarias, todas distintas.
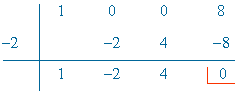
x3 + 8 = (x + 2)(x2 - 2x + 4)
Tiene una raiz real y dos imaginarias, todas distintas.
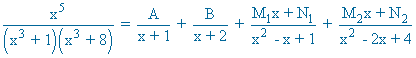
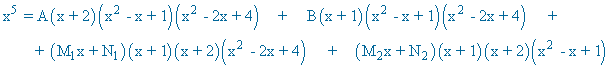
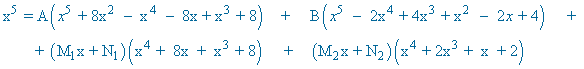
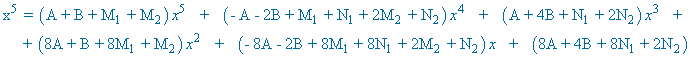
Identificamos, en ambos miembros de la igualdad, los coeficientes de x5 , x4 , x3 , x2 , x y termino independiente:
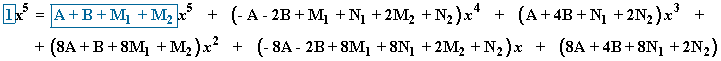
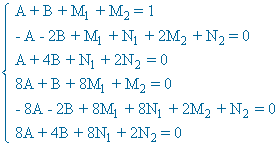
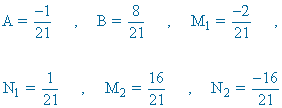
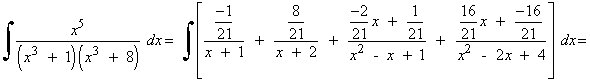
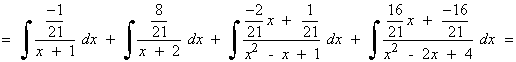
![]()
![]()
![]()
![]()
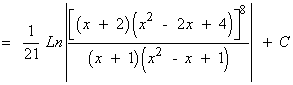
Resuelve la siguiente integral racional:
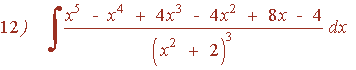
El denominador tiene raíces imaginarias multiples, por lo que la descomposición es la siguiente:
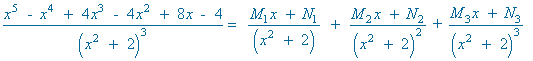
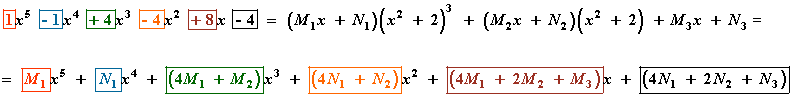
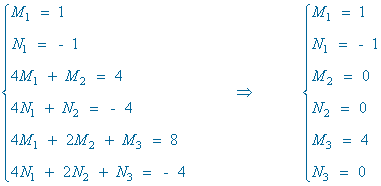
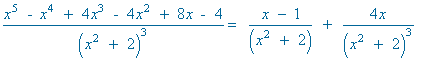
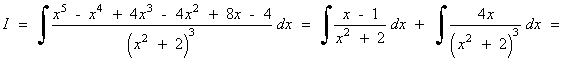
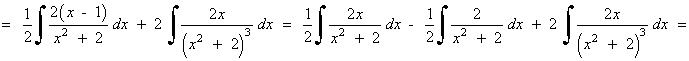
![]()
![]()
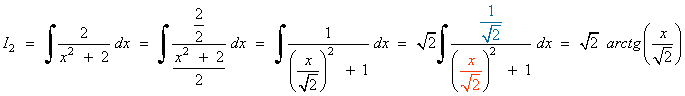
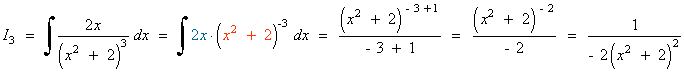
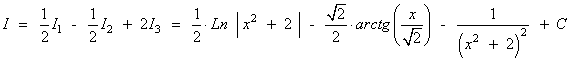
Resuelve la siguiente integral racional:
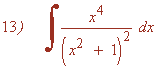
El grado del numerador es igual al del denominador, por tanto, hacemos la división y aplicamos la fórmula del cociente:
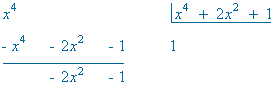
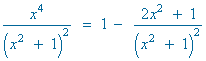
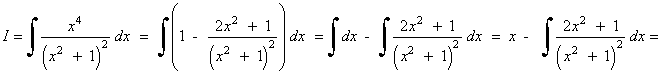
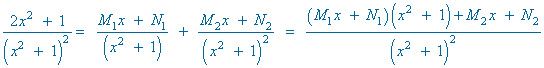
![]()
Identificamos coeficientes de x3 , x2 , x y termino independiente :
![]()
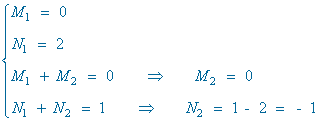
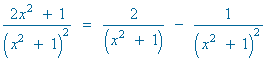
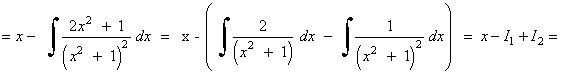
Calculamos las nuevas integrales por separado:
![]()
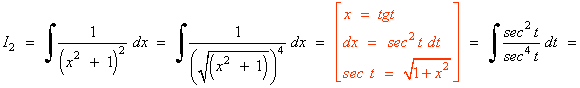
![]()
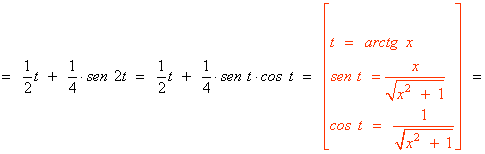
![]()
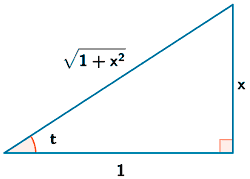
Terminamos de calcular I :
![]()
![]()
![]()
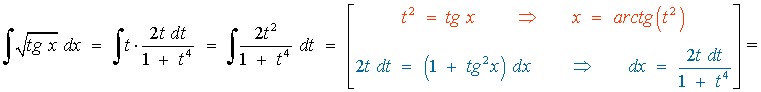
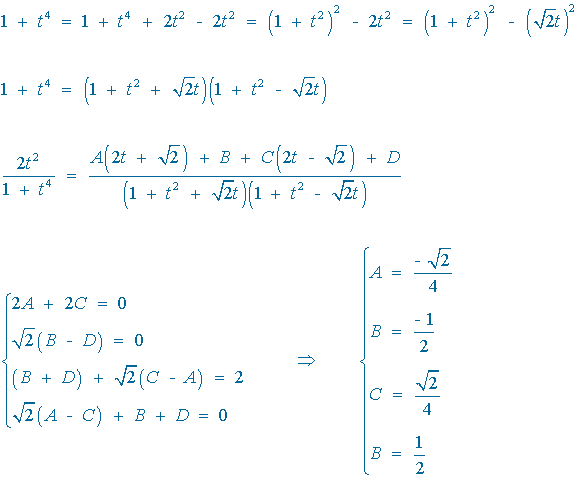
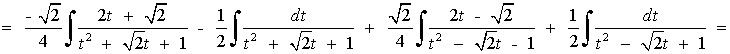
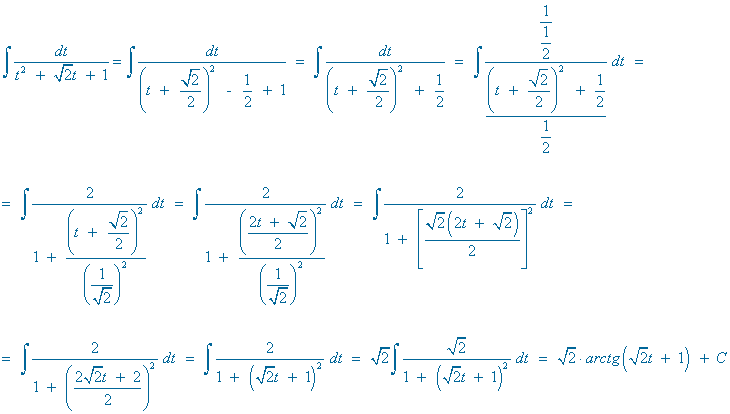
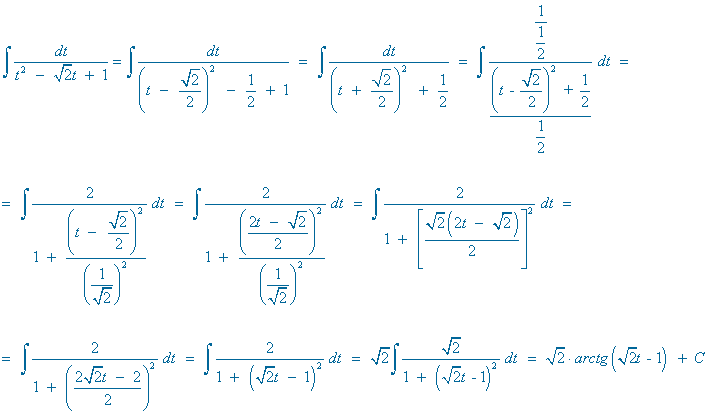
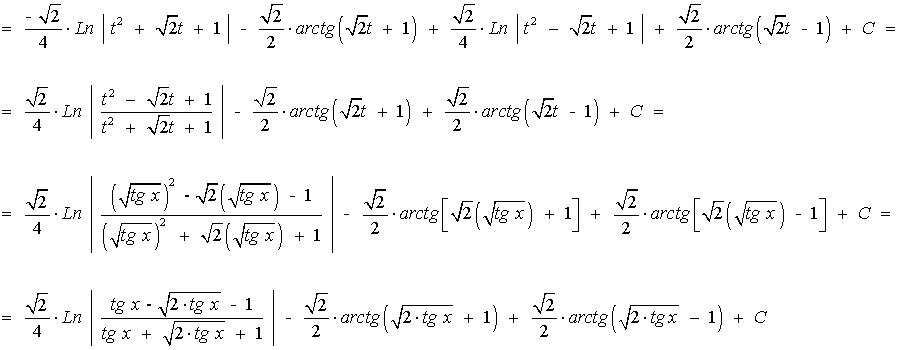


 INICIO
INICIO